基于GPS和测量机器人二等跨河水准研究与应用

曹 明，董天兵

(浙江省交通规划设计研究院，浙江 杭州 310006)

沿海地区连岛工程高程传递是当前施工和大面积地形图测绘的难点，建立统一的陆海高程基准所采用的主要手段是大跨度高程传递，即跨河高程传递。目前工程实践中，跨河高程传递方法主要有以下几种：光学测微法、倾斜螺旋法、短期验潮法、三角高程法、GPS水准和重力测量法等。常规跨河水准测量存在跨度小、多项仪器和人为误差、测量机器人测距长度有限、场地选择困难、观测操作复杂、照准目标困难，易受大气垂直遮光影响，气象因素干扰大，作业工期长，效率低；短期验潮法对验潮仪安放位置和观测环境要求较高，且观测周期较长，无法完成项目上的要求，在无高精度的局部大地水准面模型情况下GPS水准法无法完成孤岛高程传递，且GPS高程精度无法满足二等高程控制的精度要求[1-2]。

本文提出一种基于GPS、高精度测量机器人的施测方法，通过对测量目标的重新选用以及测量计算方案的优化改进，从而实现了超大跨度两台仪器光线同径向间同时对向观测，极大地消弱了大气折光和地球曲率的影响，提高了高程传递的距离、精度和作业效率。

1 跨河精密三角高程测量原理

精密三角高程测量是当前跨水域高程测量的主要方法，其是采用两台高精度测量机器人，实现对向同步观测，其高差计算公式如下[3-4]：

hAB=0.5*[(SABtanαAB-SBAtanαBA)-

(1)

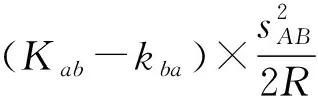
hAB=0.5*(SABtanαAB-SBAtanαBA),

(2)

在起终站上的高差计算公式为

hAB=SABtanαAB.

(3)

2 跨河精密三角高程误差来源及分析

2.1 距离误差及其影响

测距误差与仪器本身以及外界观测环境有着密切的关系，测距精度包含各种复杂的因素，为精确分析求得仅距离误差对三角高程的精度影响，特假定(3)中αAB为真值，因此得出三角高程测量主要与竖直角的精度和两点间的距离有关，且距离影响权重远小于角度精度的权；对于边长为5 km超大跨度高程传递，竖直角0°～1°范围内，最大为1.7 mm，平均约为0.87 mm，竖直角越接近0°即两点间接近水平，边长的精度和竖直角对高差的影响越小，如表1所示，因此尽量选择两侧在同一水准面上的观测点可以极大削弱距离误差对高差精度的影响。

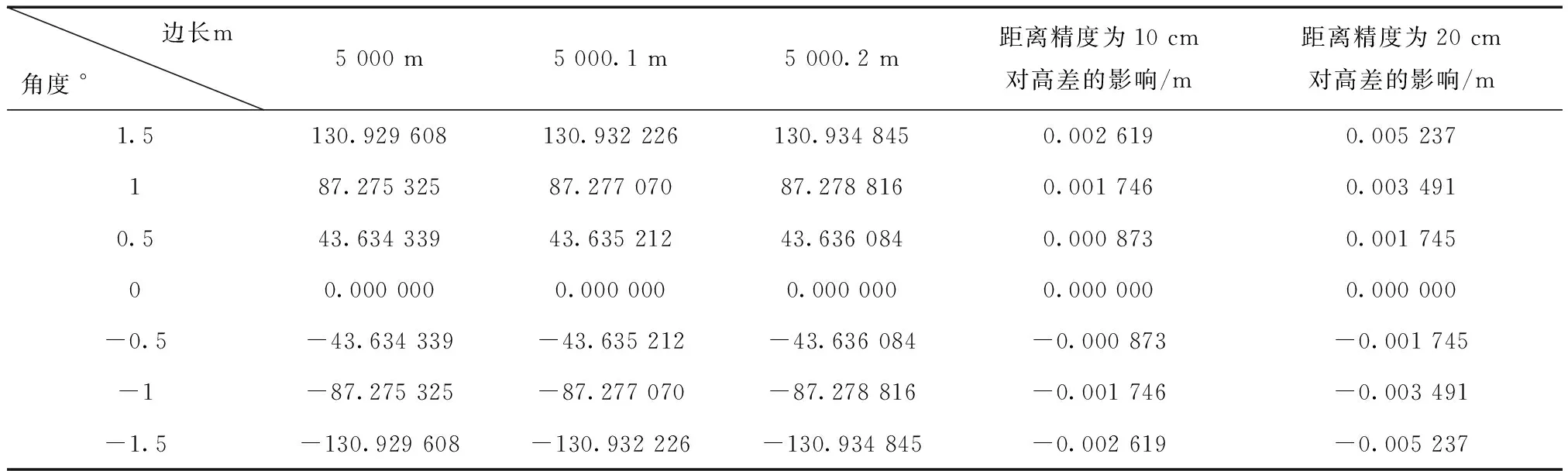
表1 竖直角与距离精度对高差的影响

2.2 竖直角误差及其影响

1)照准误差

影响竖直角测定精度的诸多因素中，照准误差影响最大，合理的观测时间和观测角度尤为重要，由于本次高程传递跨度大，已超出测量机器人测程，无法使用全站仪ATR(自动照准功能)，只能采用人工照准方式。

2)测量机器人本身误差

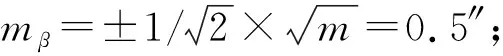
2.3 仪器高和觇牌高量取误差及影响

三角高程测量除不可避免地观测误差外，还包含仪器高和觇牌高的量取误差，即使使用专用觇牌也会存在约2 mm的偏差，此外仪器高的量取精度也会达到±2.5 mm，因此采用更加合理的观测方案和观测次序消除这项误差对于超大跨度二等高程控制就显得尤为重要。

2.4 球气差误差及影响

由于地球曲率和大气折光的存在，其严重影响三角高程的测量精度，所以必须考虑“两差”，即“球差”和“气差”的改正[9,10]。

“球气差”对所测高差的影响随着两点间的水平距离增大也越来越大，如表2所示，一般来说，两点间的水平距离超过300 m时，应考虑“双差”改正[11]。

要避免或者削弱“球气差”对三角高程测量的影响，最好的办法是采用对向观测(对向观测或往返观测)，因为相同的对向观测路径条件下，“球气差”对高差的影响相反，彼此抵消[12]。

表2 “两差”对高差的影响 m

3 鱼山大桥连岛工程二等水准施测方案

3.1 工程概述

鱼山大桥是舟山连岛工程的关键性工程，东起岱山县双合村，西接鱼山岛，其路线全长8.815 km，沿线设置一座7 781.8 m的特大桥；其中过渡岛屿花鼓山与鱼山岛之间没有任何连接岛屿且跨度约5 km，超出现有设备测程，如图1所示。

3.2 点位布设及优化

如图1所示，在花鼓山上选择一测量观测墩，用于架设测量机器人Y1；在观测墩的旁边稳定的位置架设脚架，照准点(测灯D1)安置于该脚架上；观测墩旁边路面上的铁钉S1作为临时水准点。在对面鱼山岛上选择一测量观测墩用于架设同型号设备Y2；在观测墩旁稳定的位置架设脚架，照准点(测灯D2)安置于该脚架上；此网型布设的目的在于将仪器高全部作为中间过程抵消。

值得注意的是，为尽可能保证跨海观测点间基本水平，以削弱距离误差对高差的影响，Y1与D2、Y2与D1需基本保持在同一水准面上，必要时采用似大地水准面精化模型确定；此外为最大程度削弱三角高程距离及大气折光的影响，Y1、D1及S1和Y2、D2及S2布设尽可能近。

由于本次跨海属于超大跨度，为最大程度削弱球气差对高差精度的影响，使对岸两侧Y1对D2、Y2对D1观测路径保持一致，D1、D2应尽量分别布设在Y1和Y2的延长线上；此外观测墩旁边路面上放置尺垫作为临时水准点S2，在临时水准点S1和临时水准点S2上架设等高(或同一个)观测目标或棱镜，以消除目标高度对精度的影响。如图1所示。

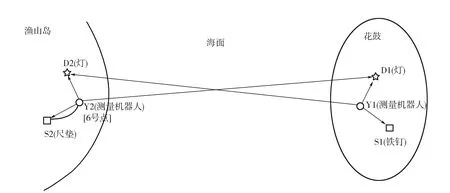
图1 跨海观测线路及观测方案略图3.4仪器选用及观测方案

根据上文中分析的误差来源，在良好的点位布设前提下，高差测量的精度主要取决于竖直角的观测精度；为最大程度削弱仪器误差带来的影响，本次选用Leica TM50超高精度智能测量机器人，其测角精度为0.5″。

本次高程传递位于大面积海域，观测条件复杂，受风、温度、湿度、水汽等影响很大，为保证外业观测质量，须根据现场气象条件和潮汐变化情况，确定观测时间和观测方案[13-14]，观测时间宜在晴朗无风的天气进行；此外本次属超大跨度，已经超出现有测量机器人测程，仪器自带的自动照准功能已无法使用，即使超大觇牌也无法清晰观测，必须对观测目标重新设计，本次提出使用发光对称的圆形灯替代常规的觇牌+棱镜的模式，为保证目标清晰，观测时间定在晴朗无风的夜间进行。

经上述分析，大跨度点位基本位于同一水准面，竖直角接近0°，其边长对高差影响极小，因此Y1—D2、Y2—D1的距离可以采用GPS静态测量测定，Y1—D1、Y1—S1、Y1—D2、Y2—D2、Y2—S2、Y2—D1的竖直角通过测量机器人观测获取。

1)大跨度边长测量。采取GPS静态观测。采样要求：时段数2个，时段长度60 min，采样间隔15 s。

2)竖直角观测。跨海段对向观测只记录竖直角，采用正倒镜测量模式。进行跨海段观测时应保证两边同步进行(从Y1测站观测对岸测灯D2，从Y2测站观测对岸测灯D1)。时段测回数规定：同岸点间观测2测回，对岸观测8组，每组8测回，共64测回；为保证观测时间一致性，若一组观测时长超过20 min，该组必须重新测量。观测限差规定：一组中各测回，竖直角指标差较差应不大于6 s，竖直角测回较差不大于3 s。观测时段要求，2个观测时段，1个检测时段，上半夜进行时段一观测，下半夜进行时段二观测，检测时段选在另一时间进行。

3)测灯D1与D2应在测回间同时变换高度，以增加观测值的可靠性，最后将S1上的棱镜杆移至S2上，保持棱镜高度不变，观测Y2与S2之间的高差。

4 数据处理及精度分析

4.1 数据处理优化

为进一步简化外业操作、设备高误差及数据处理过程，对过程中所有涉及仪器高的部分全部采用假定值，观测值均为不包含设备高的直接观测值：

hS1S2=HY2+iY1-(HS2+vS1)+0.5*

[(HD1+vD1-HY1-iY1+HY2+iy2-

HD1-vD1)-(HD2+vD2-HY2-iY2+

HY1+iY1-HD2-vD2)]+HS2+vS2-

(HY2+iY2).

(4)

式中：H为点位绝对高程，h为点间高差，i为仪器高，v为目标高，其中vS2和vS2为同一棱镜，因此vS1=vS2。

由式(4)可知，所有设备高度为中间过渡值，均可通过前后高差相互抵消，公式简化后如下(5)式所示：

hS1S2=hS1Y2+0.5*[(hY2D2+hD1Y2)-

(hY2D2+hD2Y1)]+hY2S2.

(5)

式中:h均表示测量机器人照准中心与目标中心间的高差。

4.2 数据精度分析

对式(1)进行微分处理，即

0.5*tanαSAdSBA+0.5*diA-0.5*

diB+0.5*dvA-0.5*dvB.

(6)

根据误差传播定律上式可转变为中误差结果，即

(7)

为简化明确各因素对高差的影响，取(7)式中：mAB=mBA=mS，mαAB=mαBA，SAB=SBA=S，αAB=αBA=α，根据上述，仪器和目标高没有量取误差，则上式简化为：

mh=

(8)

由式(8)可知，跨海三角高程测量误差主要来源于距离和竖直角测量精度，边长采用GPS手段进行观测，本项目采用徕卡罪行GS15型GPS也保证了观测的高精度和准确性；在跨海两侧利用似大地水准面精化模型布设在同一水平面的控制点，尽量使两点间竖直角接近于0°；由上式(8)可以得出竖直角测量精度的权远大于测距精度的权，TM50测量机器人标称精度为0.5″，其是一种误差极限的概念，在合理的观测方案下可以通过多组观测予以提高，使竖直角的观测精度提高0.1″，其成果精度可以提高1.6 mm；因此取S=5 000 m，α=1°，mα=0.5″和0.4″，mS=0.1 m，则mh=8.6 mm和mh=0.7 mm，其中各项观测误差均大于实际测量误差；二等水准观测高差限差按表3规定计算，可以得出测段、区段、路线往返测高差不符值和检测已测测段高差之差限差分别为8.9 mm和13.4 mm，因此该优化方案理论上满足二等水准精度要求。

本项目进行一段5 km超大跨度跨海高程传递，分两个时段进行，时段一和时段二分别在晴朗无风上半夜和下半夜进行，检核时段选在第二天晴朗无风夜晚进行，各时段大跨度均观测8组，数据取各组平均值，高差观测值如表4所示。

表3 水准观测限差 mm

注：k—测段、区段或路线长度，km；当测段长度小于0.1 km时，按0.1 km计算；R为检测测段长度，km。

由表4可以看出不论是各时段互差还是检核时段较差均小于规范规定限差；数据成果完全满足二等水准限差要求。

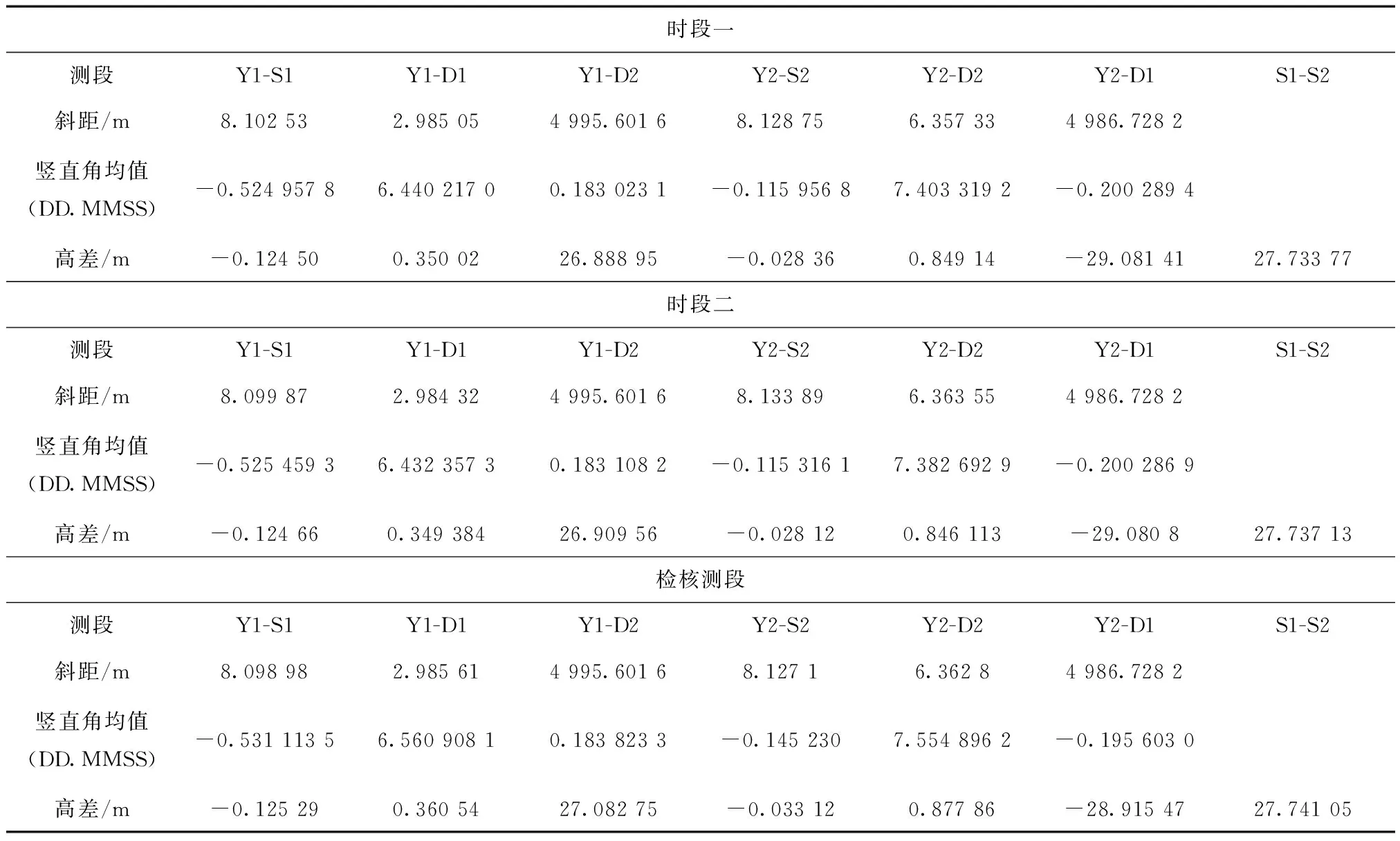
表4 各时段观测值

表5 高差成果与限差

5 结束语

对于超出测距设备测程的超大跨度连岛工程，本文提出利用GPS测边和高精度测量机器人测角的高程传递方法，研究了竖直角大小即两点间高差与边长精度之间的相对关系，即在一定高差范围内，边长精度对高差的影响很小，并进行了误差分析和预计算，得出了高差中误差计算公式，结果表明竖直角测量精度的权远大于测距精度的权，通过提高竖直角的测量精度可以大幅提高高差的测量精度；采用对向观测的同时对观测方案进行优化改进，充分保证对向观测往返为同一路径，并且避免了观测过程中对仪器高的量取，简化了作业环节，提高了成果精度，对观测成果进行了分析，结果证明成果满足二等水准精度要求。

为今后大跨度高程传递提供了准确数据和工程实践依据，具有十分重要的意义，可以通过对观测目标的进一步改进，获得更为快捷、准确的观测成果，提高高程传递距离和精度。