改进的两阶段最小二乘法在异方差模型中的应用

戴晓鸣 ，王维国

（1.东北财经大学 经济学院，辽宁 大连 116025；2.大连交通大学 理学院，辽宁 大连 116028）

0 引言

在统计分析和计量经济分析中，往往通过建立统计或经济变量之间相互关系的模型，并通过一定的回归方法对模型进行估计。一般而言，回归模型需要做一定的假设，其中随机误差项的同方差就是其中一项重要前提假设。但是，在实际回归分析过程中，随机误差项同方差的假定往往不能得到满足，也就是说，回归模型存在一定的异方差性。大多数的情况都不能充分满足随机误差项同方差这个条件的，因此大多数的模型都存在一定的异方差性。这种异方差性的存在，是多种原因共同作用而引起的，其中，模型变量选取的偏误、截面数据各单位偏差较大等因素是造成回归模型异方差的主要原因。如果在变量选取中出现重要变量疏漏，那么该变量便归入模型的随机误差项中，结果便造成了异方差。而截面数据中，各个单位之间的偏差可能较大，从而内生性地造成模型的异方差。异方差模型下，普通的OLS方法进行估计得到的结果具有明显的有偏性，这与无偏性的假设相悖，因而OLS方法已不适用。当然，目前学术界已采用多种方法检验、修正或应用于异方差模型。本文尝试提出基于正交表的方法的一种新的两阶段最小二乘法，并比较它与传统两阶段最小二乘法在异方差模型的应用。

1 传统两阶段最小二乘法对异方差模型估计

多元回归模型中，假定 (x1i，x2i，…，xpi，yi) ，(i=1，2，3，…，n)为两组样本收据。首先，要利用多元线性回归的方法，将上述模型变为一元线性回归模型。然后，对每一个线性回归模型进行异方差检验。为了具体分析模型的模型的有限性，下面引入一个自变量xi，对模型进行异方差检验。步骤1：将样本数据按照自变量的x1按照数据大小顺序进行排列，其他自变量与对应变量的相对关系保持不变。步骤2：将样本分为N组，第i组有ni个元素，则n满

步骤3：令x1i为i组的第一个自变量的组中值，x2ij为i组 的 第 二 个 变 量 ，以 此 类 推 ，满 足 定 (x1i，x2ij，…，xpij，yij) ，(i=1，2，3，…，n;j=1，2，3，…，ni)。

步骤4：假定分组数据满足如下多元回归模型：

其中，误差项为εij，满足。接着，对式（1）进行变换，等式两端同时除以σi，可得：

则误差项为εij/σi。

步骤6：进行第二阶段估计，将估计量代入变换后的新模型，则新模型的OLS系数估计量为原模型的GLS系数估计。

2 改进两阶段估计法对异方差模型估计

当样本数据较小时，通过分组产生的重复数据会导致信息失真，部分样本信息丢失，是的回归模型的精度不高。为了提高回归模型的精度，消除重复数据的影响，借鉴前人的研究，采用正交表的方法来改进二阶段估计法的第一阶段。

假定样本 (x1i，x2i，…，xpi，yi)，(i=1，2，3，…，m)，满足如下回归模型：

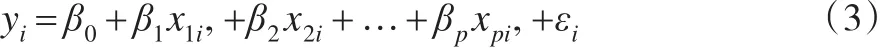
在模型（2）中，变量x1是引起异方差性的关键性变量。考虑到计算的简化性与典型性，先假定p=3，利用正交表，产生重复设局L9(34)，然后对数据按照大小顺序近分组，并进行两阶段估计。

步骤1：利用正交表获取重复数据，Δ=0.01,第i个样本数据通过变换后产生的数据如下：

步骤2：假定每一个因变量yi的观测值满足正态分布N(yi，θ2)，从正态分布中随机产生9个数据，记作yij，其中i=1，2，…，m;j=1，2，…，9;θ2=0.01 ，且yij与 (x1ij，x2ij，x3ij)相对应。

步骤3：对i个样本产生的观测值按自变量从小到大排列，其他变量与自变量的对应关系保持不变，将与第i个样本进行排序后的数据记作第i组，满足i=1，2，…，m，该组的第一个自变量的组中值为x(1i)分组后的数据为(x(1i)，x(2ij)，x(3ij))。

步骤4：利用模型（3）对数据进行变化，两边同时除以σi，可得变换后的同方差模型：

其中，εi/σi～N(0，σ2)。

步骤5：进行第一阶段估计，由于：

这里的ni为正交表的试验数，因此可采用第i组的方差估计第i个标准差的平方。

步骤6：进行第二阶段估计，将估计量=代入变换后的新模型，则新模型的OLS系数估计量为原模型的GLS系数估计。

3 改进的两阶段最小二乘法估计异方差模型的数据模拟

通过简单的数据模拟，对改进后的两阶段最小二乘法和传统的两阶段最小二乘法分别进行估计和检验，并对结果进行比较，以判断改进的两阶段最小二乘法在异方差模型应用中是否有效。

首先，假定简单的回归模型如下：

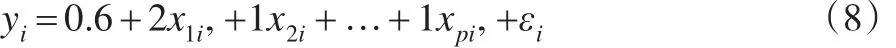
其中，i=1，2，3，…，n；随机误差项εi服从正态分布，且满足不同样本i下的随机误差项之间相互独立。根据传统的两阶段最小二乘估计方法，通过改变分组数k，便可能改变模型估计的误差。这里，分别列出当取3、6和10时的回归结果。为了使结果比较更加清晰，这里模拟时假定样本容量较小，取n=30。其中，x1i、x2i、xpi,的数据序列由本文自行给定，但限于篇幅，此处略去具体数据。

本文给出均匀分布和正态分布两种情况下的结果，具体模拟结果分别如表1、表2所示。其中MAEΣ、MAEy分别表示随机误差项的平均绝对误差、被解释变量观测值的平均绝对误差；R2为模型的可决系数；βi(i=0，1，2，3)为回归系数。

表1 均匀分布条件下的两种两阶段最小二乘法估计结果比较

表2 正态分布条件下的两种两阶段最小二乘法估计结果比较

根据表1和表2的估计结果可知，不管是采用均匀分布类型还是正态分布类型，改进的两阶段最小二乘法估计的MAEΣ、MAEy和R2值都优于传统两阶段最小二乘法，变量系数值βi也都比传统两阶段最小二乘法得到的系数值精确。由表3和表4（见下页）可以明显地看出，运用改进的两阶段最小二乘法估计得到的系数，与既定系数之间的偏差率要明显低于传统两阶段最小二乘法的偏差率。例如，对于β2而言，运用改进的两阶段最小二乘法在均匀分布条件下估计得到的系数值，与既定系数的偏差率仅为-0.77%，而用传统两阶段最小二乘法估计得到的系数值，对于k=3、k=6和k=10时，与既定系数的偏差率分别达到了-11.03%、-7.59%和-5.34%。因此，通过以上数值模拟可以充分表明，运用改进后的两阶段最小二乘法对异方差模型进行估计，得到的结果相对更加接近既定的模型参数，估计效果要优于传统的两阶段最小二乘法。

表3均匀分布条件下不同方法估计系数结果与既定系数的偏差率（单位：%）

表4正态分布条件下不同方法估计系数结果与既定系数的偏差率（单位：%）

虽然通过适当控制分组数k，可以适当降低传统两阶段最小二乘法估计异方差模型得到的误差，提高精确度，但是这比想象之中要复杂得多。从表3的偏差率可以看出，当k取值为6时，四个参数的偏差率都要小于其他两种取值（k=3和k=10）。但是，从表4偏差率又可以发现，在k取值分别为3、6、10时，四个参数的偏差率各有千秋，并不能指明到底k取值为何值时精度相对最高。在这种情况下，可能需要对k的取值进一步斟酌。在实际运用于异方差模型的过程中，这样的情况难免会对模型处理带来困难。但庆幸的是，运用改进的两阶段最小二乘法，在一定程度上可以解决这一问题。至少对于本例而言，无论是均匀分布条件还是正态分布条件，运用改进后的两阶段最小二乘法都能获得相对理想的估计结果。

4 改进两阶段最小二乘法估计异方差模型运用的实例

为了进一步从经验上证明改进的两阶段最小二乘法在运用于异方差模型时，相比传统两阶段最小二乘法更具优越性，下面本文通过一则与我国经济运行直接相关的案例进行分析。这里重点考察我国城镇居民人均服务性消费支出与收入水平、地区宏观经济发展水平、服务业发展水平之间的关系。因变量Y代表城镇居民人均服务性消费支出；自变量X1代表城镇居民人均可支配收入、X2代表地区生产总值（GDP）、X3代表第三产业增加值。

采用2015年我国31个省、市、自治区的横截面数据作为样本。首先，通过普通的OLS估计，结果如下：

yi=-0.2103+0.2861x1i，+0.1927x2i+ …+0.6383xpi，+εI（9）

其中，可决系数R2仅为0.5278，F值也仅为3.6593，通过Goldfeld-Quandt检验法和帕克检验法都显示了上述回归模型存在异方差。

下面，利用上述改进的二阶段估计模型，对这些变量进行分析。由于分组数据每组的样本数据是一定的，为了避免每个样本个数大，保证样本数据的有限性，对传统的二阶段估计法进行改进。改进后的二阶段估计不仅避免了样本个数较大的缺陷，也增强了精度。为了突出改进方法的优越性，对比原方法与改进方法的参数估计差别，分别计算因变量Y的平均绝对误差MAEy与系数R2，具体结果见表5所示。

表5 普通OLS估计法、两种两阶段最小二乘法估计法的结果比较

由表5可以看出，城镇居民人均服务性消费支出与其可支配收入、地区生产总值、第三产业增加值都呈现明显的正相关性。无论是改进的二阶段参数估计，还是传统的参数估计都的得出相一致的变化结果。具体来看，人均服务性消费支出与其可支配收入的估计系数为0.5791，说明当城镇居民人均可支配收入每增加一个单位时，城镇居民人均服务性消费支出将增加0.5791个单位。人均服务性消费支出与地区生产总值的估计系数为0.429，说明地区生产总值每增加一个单位时，城镇居民人均服务性消费支出将增加0.429个单位。人均服务性消费支出与第三产业增加值的估计系数为0.8627，说明第三产业增长值每增加一个单位时，城镇居民人均服务性消费支出将增加0.8627个单位。改进后的系数与分组的数据基本一致，相对而言，改进的数据比分组的数据更为稳定，基本位于分组数据的变动范围内。

从平均绝对误差MAEy来看，改进的二阶段估计模型的平均绝对误差更小，说明拟合程度更优，说明改进的二阶段模型更有利于因变量的值接近实际的观测值。随着分组数的增加，估计的精度也会随之提升。从系数R2来看，改进的二阶段估计模型的系数明显提高，由原来的0.9617、0.9633与0.9593提升到0.9937。由此可知，改进的二阶段估计模型能更好地解释实际结果。

5 结论

本文设计了一种基于正交表的方法的改进两阶段最小二乘法，将其应用于异方差模型中。通过比较该方法与传统两阶段最小二乘法在异方差模型的应用，发现这种新型方法具有更高的估计精度，也在一定程度上解决了传统两阶段最小二乘法在估计截面数据模型模型时因分组所带来的精度问题。因此，本文认为所提出的这种改进的两阶段最小二乘法在处理异方差模型方面具有较高的实用性。尽管如此，本文所采用的改进两阶段最小二乘法在应用于异方差模型时仍带有局限性，因为基于正交表扩大数据样本之后，也会产生新的变量随机性，也可能对估计误差带来影响。所以，在以后的研究中，需要对此问题探索新的方法，并作出相应修正，以使估计方法更加可靠。