逆抽样条件下配对试验设计中优比的统计推断
2018-10-09江绍萍李慧敏
江绍萍,李慧敏,缪 清
(云南民族大学 数学与计算机科学学院,昆明 650500)
0 引言
在生物医学研究中,人们常常想知道同一类药物的两种药品药效、同种疾病的两种处理方法的成功率是否一样?为回答上述问题,人们考虑配对试验设计下的等价性检验。如对n个患某种疾病的病人使用标准处理方法进行治疗,而对另外n个病人(与前一种治疗方法的病人有相同的病情、年龄、性别等)使用一种新的处理方法进行治疗,或对n个病人同时使用两种不同的诊断方法进行诊断,以评价两种诊断方法的检验敏感度或特异度的等价性等,这就得到一个 2 × 2 的列联表[1,2]。McNemar[3]最早采用2×2的列联表进行两种治疗方法的等价性评价问题的研究。相继的很多学者[4-7]采用风险差、风险比、优比等进行治疗方法的非劣性和等价性检验问题的研究。
上述研究是建立在抽样总数固定的基础上进行的,然而,实际临床实验中,经常遇到小概率问题,如一些罕见的疾病。此时若抽样总数固定,则抽样中可能会出现列联表的某些格子里样本数很少甚至为零的情况,从而使得样本落入相应格子的概率的极大似然估计为零(而实际中并非为零)[2];或者人们感兴趣的是其中一个格子抽到r个病例的情况,而此时的抽样总数可能不是获得感兴趣r个病例时所需的最小抽样总数,这不仅有悖于道德伦理,也造成资源浪费。为避免上述情况,在2×2的列联表研究中,采用逆抽样(也成为负二项抽样)进行数据处理,既符合实际理论的需要,又兼顾道德伦理的合理性[2]。所谓逆抽样,就是事先确定感兴趣的样本数,然后持续地进行抽样,直到感兴趣的样本数达到预先规定的数目。近年来,众多学者[8-10]对逆抽样条件下基于两独立样本试验设计的2×2的列联表数据进行了多方面研究,而对逆抽样条件下配对试验设计2×2列联表的研究成果较少。因而本文把逆抽样方法加入到配对试验设计2×2列联表,通过优比进行统计推断问题的研究。
1 概率密度函数及优比的定义
假定治疗某种疾病有两种治疗方案(称为标准治疗方法和新方法),每种治疗方案都是一个二分量变量(即治疗成功和治疗失败,分别记为1和0)。在抽样过程中连续抽样直到获得x01(≥1)个标准治疗方案成功而新治疗方法失败的样本时才停止抽样,由此得到配对的2×2列联表如表1所示:
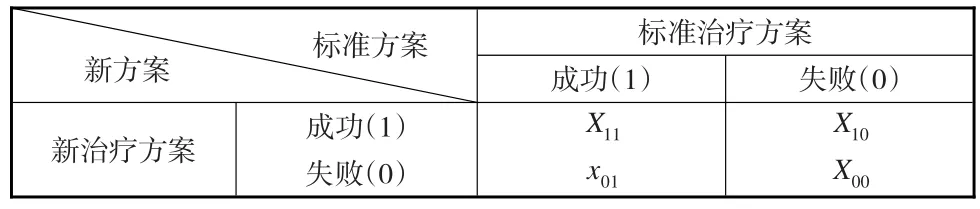
表1 某疾病新旧治疗方案检验结果
其中x01是先前固定的正整数,随机变量X11,X10和X00表示配对试验设计中当获得x01个先前固定的样本时落入其他相应格子中的样本数。记π11,π10,π01和π00分别表示配对试验设计中样本落入相应格子的概率。随机变量X11,X10和X00的联合概率密度函数为:
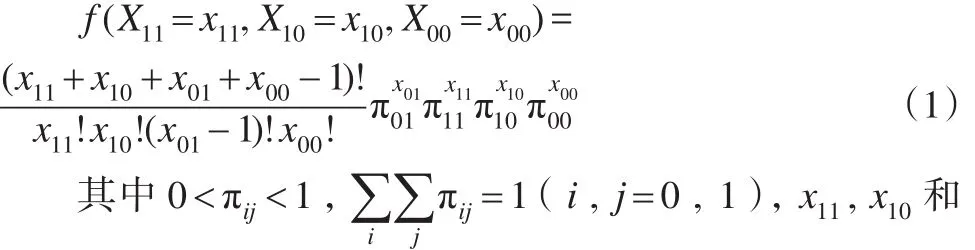
x00的取值分别为 0 , 1 , 2 。
根据Lachin[11]定义优比(Odds Ratio)为
因此,本文的假设检验为:

其中δ0为一个已知常数。根据优比的定义,得到π10=δπ01。因而观测频数 (x11,x10,x00)的对数似然函数为:

其中c为不依赖于参数δ和π01的常数,δ为感兴趣参数,π01为讨厌参数。
2 参数估计及统计量的建立
2.1 参数估计
记θ=(δ,π01),对数似然函数关于参数的一阶导数和二阶导数分别为:
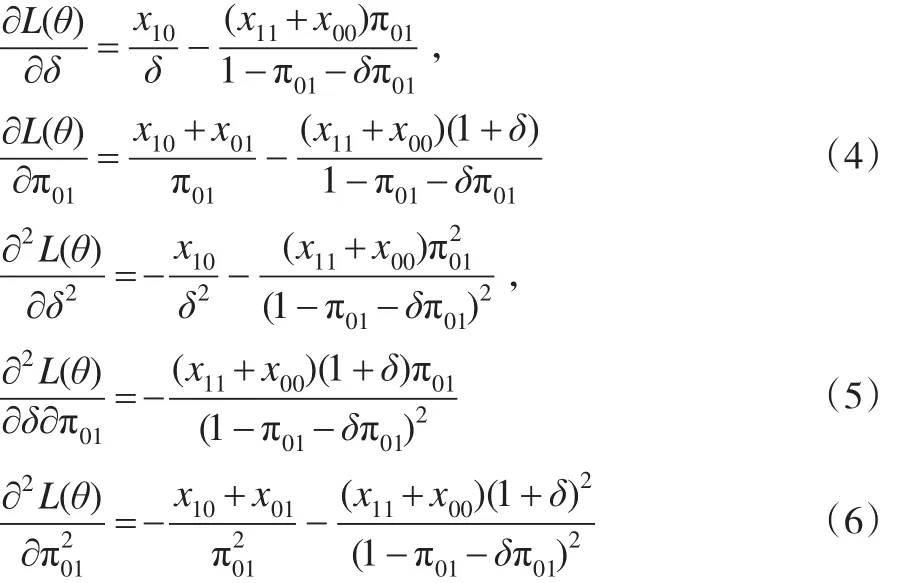
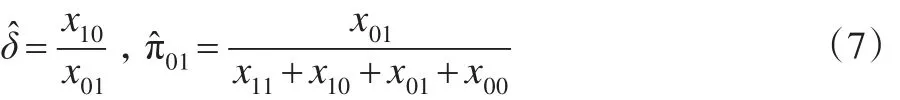
同理,可以求解在H0:δ=δ0条件下讨厌参数的限定性极大似然估计。此时令,得到限定性条件下参数极大似然估计记,其中:
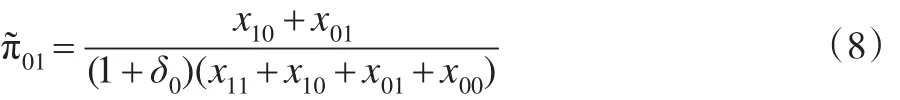
2.2 检验统计量的建立
以往通常采用delta方法求解感兴趣参数的期望和方差,但delta方法是一种近似求解的方法,得到的结果带有一定的偏差;为了避免出现这种偏差,文中采用Fisher-score的方法求解参数的方差。由此建立Fisher信息阵如下:

计算上述Fisher信息阵时,应注意到随机变量x1j(j=1 , 0)服从参数为x01和的负二项分布,x00服从参数为x01和的负二项分布。通过求解Fisher信息阵的逆矩阵得到感兴趣参数的方差为:

从而得到:
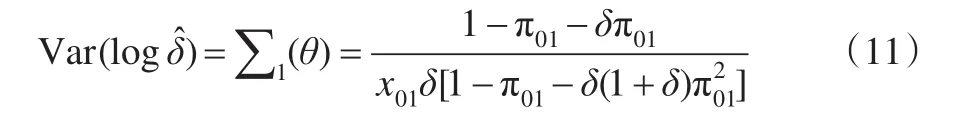
故建立六个检验统计量如下:
(1)Wald检验统计量(基于样本方差):

(2)Wald检验统计量(基于原假设下方差):
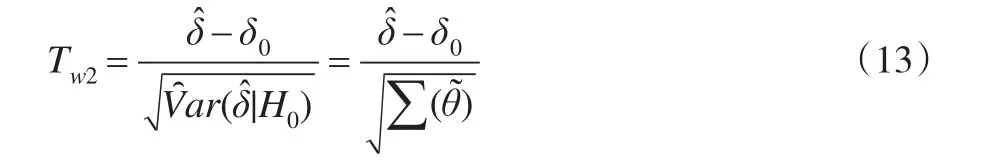
(3)对数Wald检验统计量(基于样本方差):
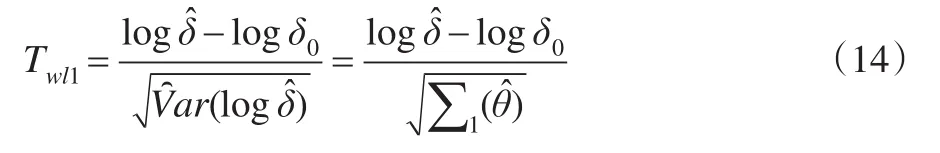
(4)对数Wald检验统计量(基于原假设下方差):

(5)Score检验统计量:

(6)似然比检验统计量:
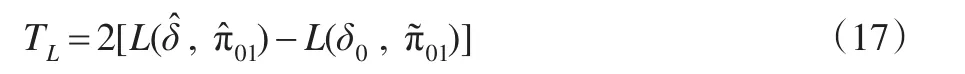
上述Wald型检验统计量、对数Wald型检验统计量渐进服从标准正态分布,而Score检验统计量和似然比检验统计量渐进服从自由度为1的卡方分布。
3 模拟研究
通过模拟研究比较上文提出的检验统计量的有效性,即通过在相同的样本量和在各种参数设置下,产生10000个随机数,并且计算这些检验统计量的经验第一类错误率和经验功效。如果经验第一类错误率和事先给定的显著性水平比较接近,则认为该检验统计量比较有效。在计算犯第一类错误的概率时,优比的取值为1.0,2.0,讨厌参数π01的取值为0.05,0.1,0.15和0.2,样本量的取值为10,20,30,50,80和100。在计算功效时,δ0=0.8 ,讨厌参数 π01的取值为0.05,0.1,0.15和0.2,样本量的取值为10,20,30,50,80和100。计算的结果如下页表2和表3所示:
为了衡量模拟检验的效果,根据Tang等[12]中讨论,如果经验第一类错误率与名义第一错误率的比值超过1.1(即显著性水平α=0.05而经验第一类错误率大于0.055)时,称为“宽松检验”;如果经验第一类错误率与名义第一错误率的比值小于0.9(即显著性水平α=0.05而经验第一类错误率小于0.045)时,称为“保守检验”;否则称为“稳健检验”。所以根据表2和表3得到如下结论:(1)Wald统计量(基于原假设下方差)和Score统计量是稳健的;(2)Wald统计量(基于样本方差)和对数Wald统计量(基于原假设下方差)是宽松的;(3)随着样本量x01和π01的增加,经验第一类错误率越接近于显著性水平;(4)参数δ0和π01的值固定后,各统计量得到的功效随着样本量x01的增加而增大。(5)参数δ0=0.25时,Score统计量计算得到的功效是最大并且犯第一类错误的概率更接近于显著性水平。综上所述,Score统计量具有较好的性质,在以后的研究问题中是可以采纳的检验统计量。
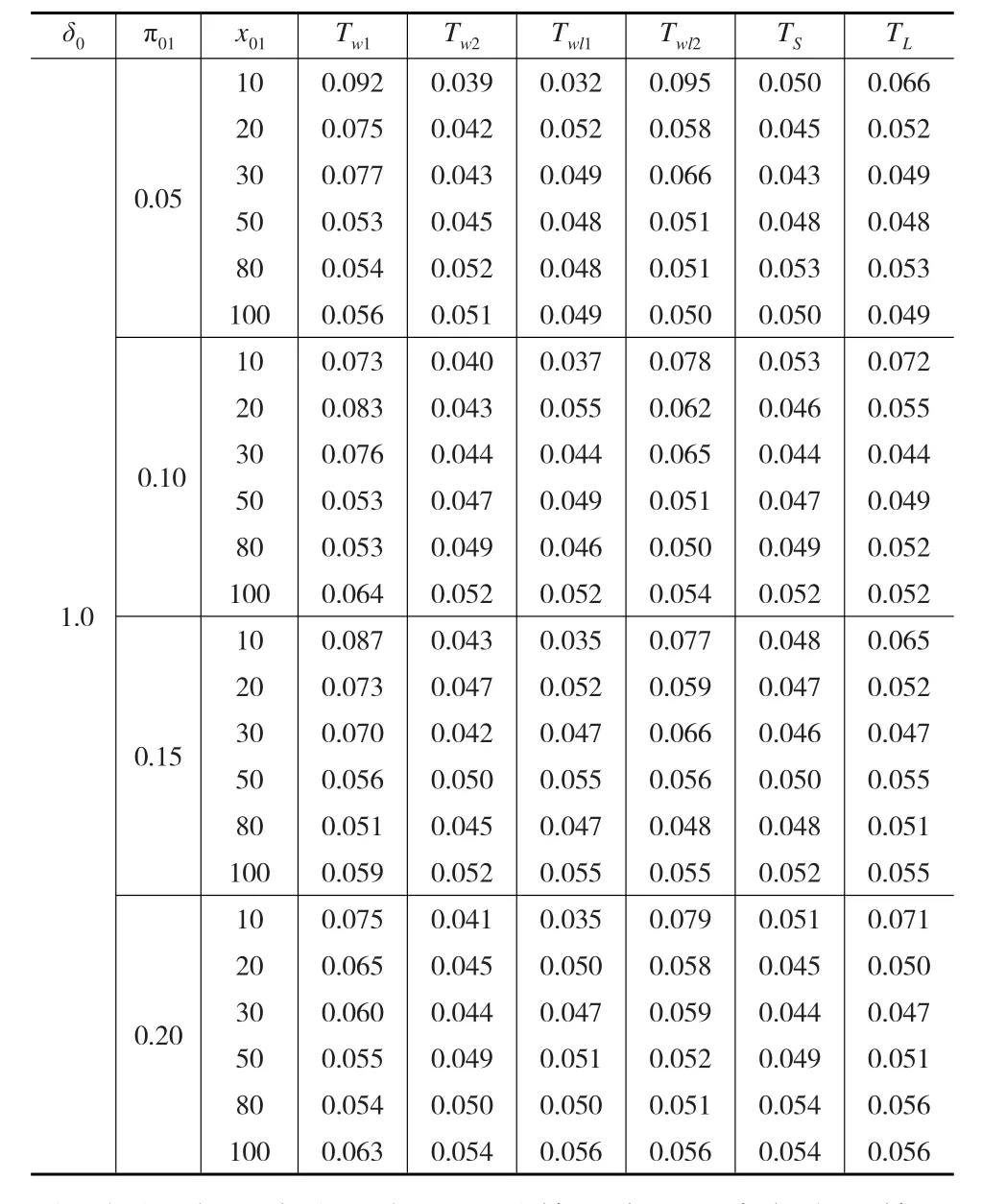
表2假设检验H0:δ=δ0和显著水平α=0.05下由10000个样本计算得到的犯第一类错误的概率
4 结束语
现实生活中经常遇见逆抽样问题和列联表数据问题,以往都是单独考虑这两个问题,本文把两者结合在一起进行优比的统计推断研究,这为列联表数据的研究提供了一种有效方法。通过模拟研究讨论了文中引进的六个统计量所使用的条件,为以后的研究提供了参考。另外,生物医学研究中的等价性评价问题除了转化为相应统计指标(如优比、风险差、风险比等)进行假设检验外,还可以在后续研究中对逆抽样条件下配对试验设计的列联表中相应统计指标进行区间估计问题研究。
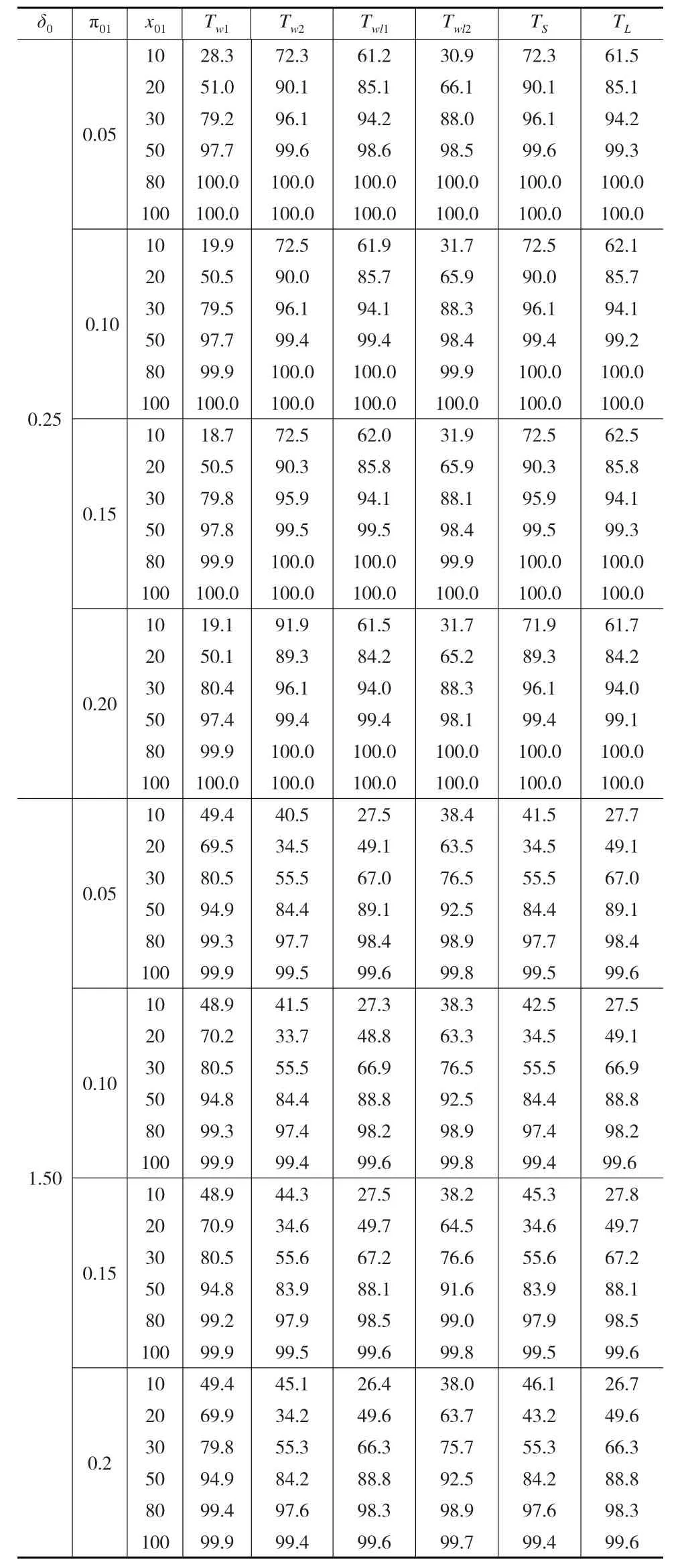
表3 假设检验H0:δ=δ0和显著水平α=5%下由10000个样本计算得到的经验功效,其中δ1=0.8
