一元二次不等式的多元化解决方法探究

河北省邯郸市第一中学 潘向宸

一元二次不等式是含有最高次数为2的未知数的不等式，它的一般形式为ax²+bx+c＞0或ax²+bx+c＜0（a≠0）。一些同学对一元二次不等式的理解存在误区，并没有掌握一元二次不等式背后的核心概念，导致其在遇到相关题目后手足无措、心慌意乱。如果在考试中发生上述情况，小则拉低自己的整体分数，大则会紊乱自己的心绪，影响正常的考试发挥。下面我将结合自身实践经验，从三种思想着手探究解决一元二次不等式的方法，即数形结合思想、分类讨论思想和方程转化思想，从而为处于迷惑或者困惑中的同学提供新的思考角度。

一、数形结合思想

数形结合思想是将数与形结合与对应起来的一种数学思想，其旨在通过形象生动的几何图形，让我们明白比较抽象的数学关系，往往采用直角坐标系进行表示，我们会比较直观地感受到其存在的数量关系，从而顺利解出数学题目。

利用数形结合思想解决一元二次不等式的具体方法：先要确定不等式两边的表达式分别是什么；其次，根据具体的表达式做出相应的函数图像；最后，具体问题具体分析，结合不等式的条件判断满足不等式的区域，这个区域就是不等式的解集。

例如：求解不等式：x2-5x＞6。

第一步：先将题目中的一元二次不等式转化为等式，并确定题目中的函数表达式是哪些，即将x2-5x＞6转化为|x2-5x|=6，计算可知x有四个解：x1=-1、x2=2、x3=3、x4=6,然后从中明确y1和y2的表达式分别是y1=|x2-5x|、y2=6。

第二步：根据x的解和上述两个函数表达式作出相关图像，如下图：

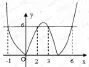
第三步：我们从图中可以发现此一元二次不等式的解集是x＜-1或2＜x＜3或x＞6。

数形结合方法是一种比较便利的解题思想。但是，部分同学容易忽视题目中的细节问题，他们会因为一时疏忽而遗漏某个不等式存在的条件，从而犯下错误，这是广大学子值得注意与思考的地方。

二、分类讨论思想

分类讨论思想是针对一元二次不等式的存在条件出现的所有可能情况分层次地展开讨论。如果二次项系数含有参数，题目中也没有明确指示，那么就要对此参数是否为零做出讨论；如果一元二次不等式中的参数不明确，那么就要对判别式分大于零、小于零或者等于零这三种情况进行判断；如果含有参数的一元二次不等式可以转化成a（x-x1）（x-x2）这种形式，那么就要对x1与x2的关系加以讨论，即x1＞x2，x1=x2以及x1＜x2。利用分类讨论思想解决一元二次不等式题目时，往往需要进行一次以上的讨论，一般来讲，如果二次项系数含有参数，先要对二次项系数是否为零进行讨论，然后分析不等式是否可以进行因式分解，如果可以进行因式分解，那么就要对一元二次不等式的两根展开讨论，如果不可以进行因式分解，那么就要对判别式的正负情况展开讨论。

首先，观察这道题目的特点，确定考查的知识点，这道题目不仅考查学生是否了解一元一次不等式和一元二次不等式的求解方法，而且还考查了学生是否会利用分类讨论思想求解题目。

其次，明确此题目中的分类情况以及分类标准，题目中含有字母系数a，我们要对a进行分类，即a=0和a≠0的情况，而a≠0又可以分为a＞0和a＜0的情况。

最后，我们按照分类情况将不等式进行变形，然后解出最终答案。

第二种情况： ，原不等式变形为 。

有时候为了更好地运用分类讨论思想，我们可以将其与数形结合思想进行互相融合、有效统一，从而快速解答一元二次不等式问题，以便节约我们的做题时间。

三、方程转化思想

方程转化思想是指将一元二次不等式转化成相应方程，然后以此为依据求解方程的根，在根的基础上寻找一元二次不等式的求值范围。方程、不等式与函数是成一体化的系统知识，我们需要对三者之间的关系进行整合和总结，从而在考试中发挥自己的优势，以便为以后的学习奠定扎实基础。

例如：解不等式 x2-x-1＜0 。

首先，我们可以将一元二次不等式转化成方程，即x2-x-1＜0，x2-x-1=0，然后求出方程的两个根，即x1=1或者x2=2。

其次，在解答出相应的根之后，我们再结合小于零的取值区间寻找具体的答案，即看此一元二次不等式的取值范围是哪部分小于0，有时候可以做出相应函数图像进行求解，或者直接整体代入进行解决，也或者进行分类讨论求出答案。

最后，x的取值范围分为三种情况，即x＜1，1＜x＜2，x＞2，我们根据这三种情况代入某个具体数值，验证此一元二次方程是否可以满足不等式小于零的情况，最终确定x的取值范围。但是，我们还要注意此不等式是否可以出现x等于零的情况，可以直接将零代入式子中进行验算，当x=0时，x2-x-1=-1，这也就说明x是可以等于零的。

以上是我针对一元二次不等式的多元化解决方法所做的总结。一元二次不等式是高中数学知识体系中较为关键的理论结构，其常常与函数、方程等内容配合出题。如果我们没有弄懂一元二次不等式的性质、特点、属性等知识，那么就会影响后面章节的学习，从而无法打牢自己的数学地基。当然，由于我的知识水平有限，文中尚有概括不到位的地方，还望老师、其他学子提出指正意见，以便督促我不断地提高自身素质。