旋转稳定二维弹道修正弹落点预测制导方法研究

2018-10-08钟扬威王良明史祥鹏

火炮发射与控制学报 2018年3期

钟扬威，王良明，国晨，叶昌，史祥鹏

(1.中国航天科工集团第九总体设计部，湖北武汉 430040; 2.南京理工大学能源与动力工程学院,江苏南京 210094;3.凌云科技集团有限责任公司,湖北武汉 430040)

落点预测制导是根据弹丸飞行过程中某一时刻的位置、速度等信息计算弹丸在无控状态下的落点位置，并与目标点位置进行对比，利用偏差值作为反馈形成制导指令的方法，目前已被用于脉冲矢量控制及鸭舵控制的尾翼稳定弹[1-2]。

对于尾翼稳定弹，其弹轴在控制力矩作用的平面内摆动，使得控制力矩方向与弹丸受控以后的摆动方向和质心运动轨迹之间的关系简单明确。因此，只需要知道预测落点相对目标点的方位角，就能得出控制力所要施加的方位角。对于旋转稳定弹，由于弹体高速旋转的陀螺效应，弹轴的摆动为二圆运动，高低和方向攻角形成复杂的外摆线运动。控制力实施后，弹轴将向垂直于控制力矩作用的平面内摆动，使弹轴产生空间章动和进动，使得控制力矩方向与弹丸受控以后的摆动方向之间的关系变得十分复杂。因此，需对在控制力作用下，旋转稳定弹的角运动、质心运动规律研究透彻后，才能提出合适的落点预测制导方法。目前相关学者对该类弹丸的落点预测方法[3-4]、落点运动规律[5-6]进行了研究，对落点预测制导的研究还比较欠缺。

笔者以安装固定舵修正引信的旋转稳定二维弹道修正弹为对象，根据其运动特点，分析了弹丸在固定舵作用下的攻角运动、速度方向运动及落点运动特性。提出了通过两次落点预测得到修正一次落点偏差所需的固定舵滚转角的方法。最后在两个射角下对制导方法进行了仿真分析。

1 有控时弹丸的角运动及落点运动的规律

1.1 有控时弹丸的角运动规律

根据旋转稳定二维弹道修正弹的质心运动方程和绕质心转动方程，可以推导得到弹丸的复攻角运动方程为[7]

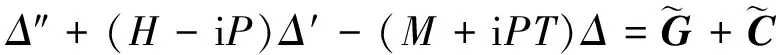
(1)

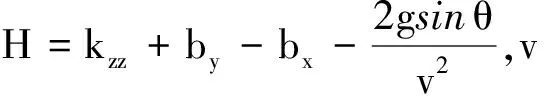
有关符号的表达式为

(2)

式中：m、S、l、d分别为弹丸的质量、参考面积、参考长度、参考直径；ρ为空气密度；CD、CLα、CMα、CMq、CMpα分别为弹丸的阻力系数、升力系数导数、静力矩系数导数、赤道阻尼力矩系数导数、马格努斯力矩系数导数；CNδ、CMδ分别为固定舵的升力系数和俯仰力矩系数对固定舵安装角δz的导数。

固定舵产生阶跃控制激励时，零初始条件下，由固定舵产生的角运动方程可写为

Δ″+(H-iP)Δ′-(M+iPT)Δ=K·ε(s)

(3)

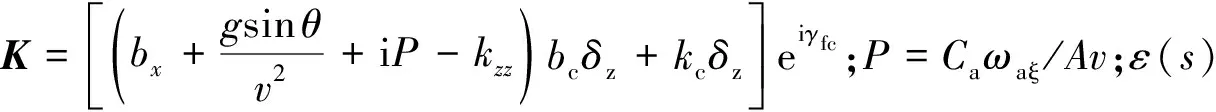
阶跃激励是一个突加的常值激励，设立新坐标：

(4)

将式(4)代入到式(3)，得：

Δn″+(H-iP)Δn′-(M+iPT)Δn=0

(5)

式中，Δn0=K/(M+iPT)，Δn0′=0。

由式(5)可见，角运动在阶跃激励作用下的响应为Δn0=K/(M+iPT),Δn0′=0的自由运动。于是得到阶跃激励作用时固定舵产生的角运动为

(6)

式中：s为弹道弧长;l1=λ1+iω1，l2=λ2+iω2,λ1、λ2分别为快慢圆运动的阻尼，ω1、ω2分别为快慢圆运动的频率。

1.2 有控时弹丸的落点运动规律

固定舵产生控制力后，弹丸的攻角会发生变化，并在攻角面内产生升力。由于攻角面不断绕速度线旋转，升力方向也就不断地改变，于是速度方向也在不断旋转改变。引入复偏角Ψ=Ψ1+iΨ2，推导可得到在固定舵作用下，偏角平均位置的相位角Φψ与固定舵滚转角γfc的关系为

Φψ=γfc+χ

(7)

式(7)说明偏角平均位置的相位角较固定舵滚转角超前了一个前置角χ。限于篇幅，具体的推导过程及χ的计算公式见参考文献[7]。

图1为某特征点上固定舵滚转角固定在0°时(升力面向上)，弹丸的偏角曲线。可以看出偏角平均位置的相位角较固定舵滚转角提前了大约155°。

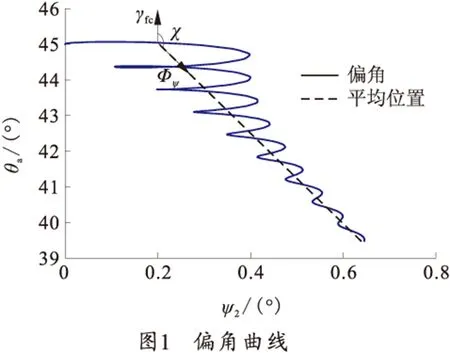
通过数值仿真，计算出35°和51°射角时，在全弹道上的变化情况,如图2所示。从图2可以看出，前置角χ在第2区间内变化，和文献[8]理论分析出的规律一致。

攻角产生的升力使弹丸的速度方向发生变化，然后改变弹丸质心位置。和对速度方向的影响一样，固定舵对质心位置的影响也不在固定舵升力面作用的方向上，而是较固定舵滚转角超前了一个角度χp。图3为51°射角时，启控时间设为20、40、60、80 s，落点修正距离随固定舵滚转角指令的变化曲线。从图3可以看出，固定舵滚转角固定在0°时，会使弹丸的射程减小，侧偏增大。固定舵滚转角固定在不同角度时，落点修正量的相位角较固定舵滚转角都超前了一个角度。

由于射程和侧偏是弹丸在全弹道飞行过程中逐渐累积产生的，而这个过程中，弹丸的速度、气动参数、转速等都在变化，这种变化又不能用简单的函数表示，因而不能得到χp的解析表达式。因此，落点预测制导的重点是如何得到这个角度，从而确定修正落点偏差所需的固定舵滚转角。

要实时求出χp，笔者提出的方法是通过两次落点预测来实现。第1次采用无控落点预测，得到预测落点p1的坐标(xp1,zp1)。第2次进行有控状态下的落点预测，将固定舵滚转角设为0°，作用在全弹道上，得到落点p2的坐标(xp2,zp2)。则可以得到两次落点预测的落点偏差：

(8)

由落点的偏差计算得到落点修正量的相位角相对于固定舵滚转角的前置角χp为

(9)

通过数值仿真，计算出35°和51°射角时，χp在全弹道上的变化情况,如图4所示。从图4可以看出，前置角χp同样在第2区间内变化。

2 落点预测模型

由于重力非齐次项作用，二维弹道修正弹产生动力平衡角δ1p、δ2p。它们将使质心速度方向改变，进而使弹道发生扭曲，产生偏流并影响射程。因此，笔者采用考虑动力平衡角影响的扩展质点弹道模型作为落点预测弹道模型，其形式如下：

(10)

式中各参数的含义及计算公式见参考文献[9]。

风产生的攻角为

(11)

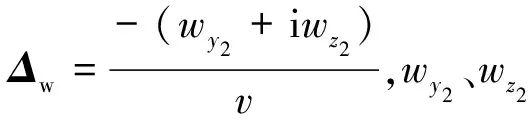
无控落点预测时，扩展质点弹道模型中的攻角为

(12)

有控飞行时，攻角还需考虑由固定舵产生的攻角

(13)

因此，有控落点预测时，扩展质点弹道模型中的攻角为

(14)

3 旋转稳定二维修正弹落点预测制导方法

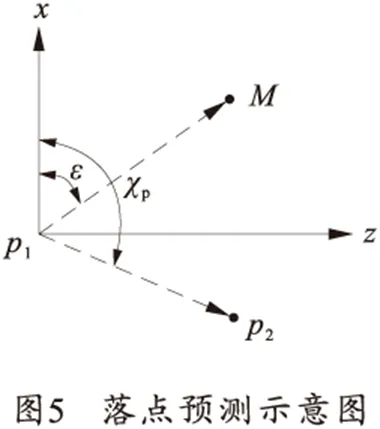
旋转稳定二维弹道修正弹落点预测制导的实施步骤是：当弹道需要修正时，先进行一次无控状态下的落点预测，得到预测落点p1的坐标(xp1,zp1)。然后将固定舵滚转角设为0°，进行一次有控状态下的落点预测，得到落点p2的坐标(xp2,zp2)，如图5所示。设目标点M的坐标为(xM,zM)，则得到目标点和无控预测时落点的偏差为

(15)

可得到落点偏差的方位角ε为

(16)

则修正落点偏差所需的固定舵滚转角为

γfc=ε-χp

(17)

式中χp通过式(9)计算得到。

4 仿真算例

以某型旋转稳定二维弹道修正弹为对象进行了大量落点预测制导仿真，限于篇幅仅给出两组算例，其中拉偏参数如表1所示，测量及控制偏差如表2所示。升弧段落点预测的时间长，因此在升弧段一次预测修正的时间间隔取为5 s,降弧段取为2 s，高度小于3 000 m后取为1 s,高度小于50 m后停止修正，弹丸以惯性飞行。

表1 拉偏参数

表2 测量及控制偏差

4.1 35°射角时的仿真分析

35°射角时，从出炮口15 s开始修正，得到的仿真结果如图6～10所示。

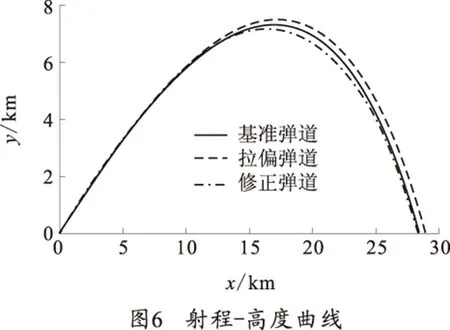
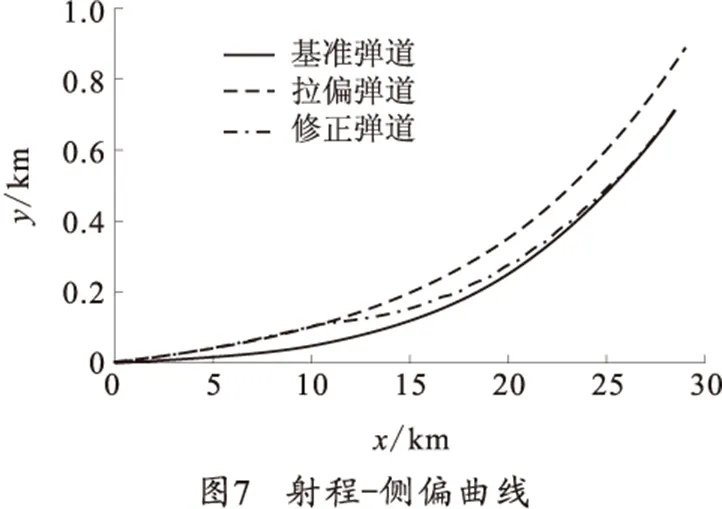
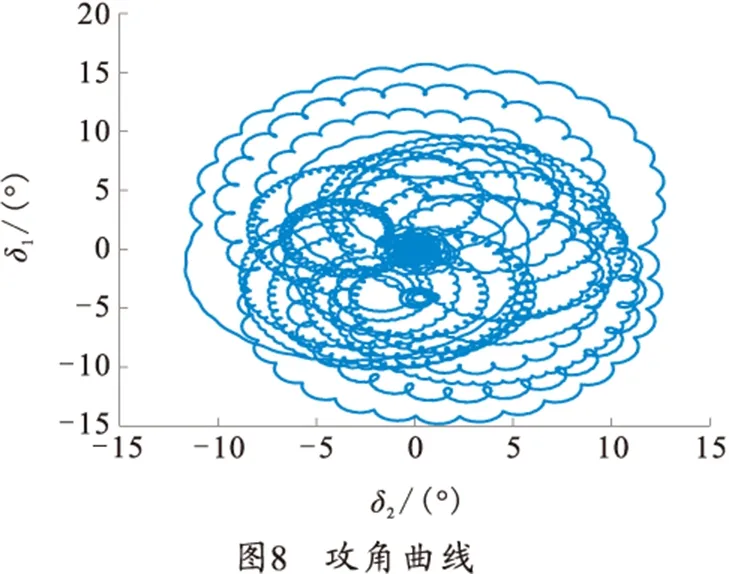
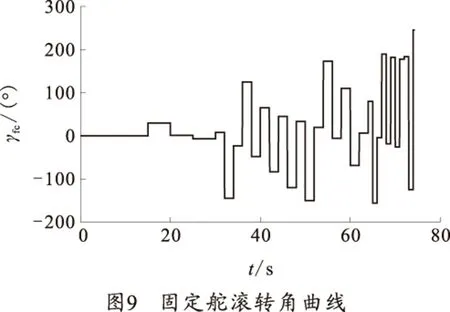
从图6、7可以看出，35°射角时，拉偏弹道的落点偏差为(507 m,210 m)。15 s开始修正后，修正弹道的落点偏差为(-8 m,2 m)。从图8看出，修正弹道的攻角呈现复杂的外摆线运动。从图9看出，固定舵滚转角变化缓慢，便于进行滚转控制。从图10看出，预测的落点刚开始都偏离实际目标点较远，但随着落点预测制导的进行，预测的落点离目标点的偏差越来越小，最后在目标点附近振荡。