基于交互式“当前”统计多模型的机动目标跟踪算法

杨 维，周 宇，王 越，林利红，石德乾，史国清

(1.西北机电工程研究所, 陕西 咸阳 712099；2.中国人民解放军63850部队，吉林 白城 137001；3.北方科技信息研究所，北京 100089)

空袭目标类型一般有巡航导弹、制导炸弹、歼击机、直升机和无人机等典型目标，随着技术及战争形态的发展，未来战场空袭平台将大量呈现无人机和精确制导武器。精确制导武器包括制导炸弹、巡航导弹、空地导弹和反辐射导弹等类型；典型制导弹药类目标的攻击方式主要有无动力滑翔攻击弹道、跃升俯冲攻击弹道，蛇形机动攻击弹道以及各种组合攻击弹道。笔者主要针对巡航导弹类目标，对蛇形机动攻击弹道建模[1-3]，在此基础上展开机动目标的跟踪和预测技术研究。

1 蛇形机动攻击弹道建模

蛇形机动是一种平面的正弦摆式机动，能够有效躲避攻击，提升突防概率，提高作战效能，是亚声速巡航导弹Block4、布拉莫斯空地导弹、AGM-88E反辐射导弹末端突防常用的攻击方式。

蛇形机动在弹体坐标系内的常用数学模型可表示为：导弹质心在主航向匀速直线运动，速度为va，蛇形机动幅度为R，初始相位为φ，坐标时域变化规律为

(1)

弹类目标相对于地面防空武器的位置应采用大地坐标系来表示，弹道方程需要将弹体坐标系转换成大地坐标系的值，其中ψ、θ指前进方向的方位角和高低角，K为导弹运动平面与垂直铅垂面的夹角。K、ψ、θ为两个坐标系之间的旋转矢量，平移矢量为(x0,y0,z0),则弹体坐标向大地坐标转换公式为

(2)

2 交互式“当前”统计多模型算法

笔者拟采用交互式“当前”多模型算法(ACS-IMMKF)，选取不同机动频率的当前统计模型作为子模型，然后融入交互式多模型算法中，通过对这些子模型的相互作用进行加权，可自适应跟踪不同环境、不同类型、不同机动程度的目标。

2.1 改进的“当前”统计模型

当前统计模型[4]实质上是一种非零均值时间相关模型，其机动加速度的“当前”概率密度采用修正的瑞利分布描述，非零均值加速度为[5]

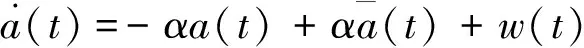
(3)

式中，α为机动频率，通常取经验值。对于慢速转弯，α=1/60；对于逃避机动，α=1/20；当α=0，该模型转变为匀加速模型。

经过离散化的当前统计模型状态方程为

X(k)=F(k,k-1)X(k-1)+

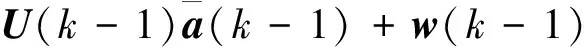
(4)

式中，F(k,k-1)为状态转移矩阵，

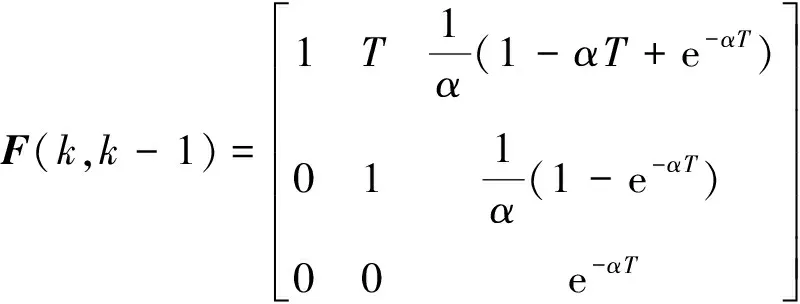
(5)

U(k-1)为输入控制矩阵，

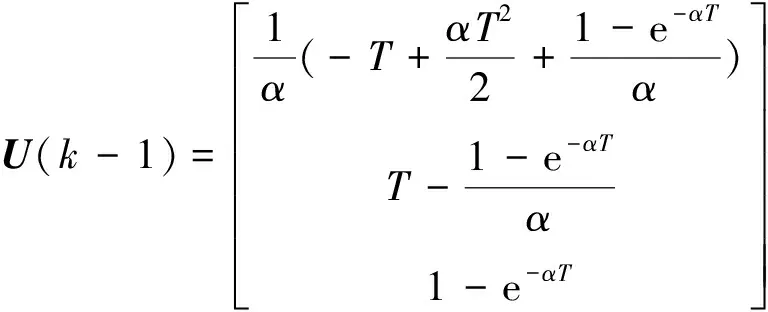
(6)

X(k-1)为目标状态向量，

(7)

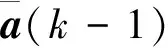
(8)

(9)

为克服常规当前统计模型算法对加速度极限值的依赖，引入高斯隶属函数对方差极限值进行修正，修正因子基于新息构造：

v(k)=Z(k)-HX(k|k-1)

(10)

式中：Z(k)为时刻k的量测矩阵；H为观测矩阵；X(k|k-1)为一步状态预测矩阵。

新息协方差矩阵：

S(k)=HP(k|k-1)HT+R(k)

(11)

计算归一化新息的范数：

g(k)=vT(k)S(k)v(k)

(12)

当目标发生机动时，g(k)增大，因此可以用前后两个时刻信息范数g(k)和g(k-1)的差异来表示目标机动的强弱。当目标机动较弱时，前后两个时刻的新息范数差异较小，模型参数也应较小并且变化较缓慢；当目标机动越强时，前后两个时刻的新息范数差异越大，模型中的各参数也应随之迅速增大以满足对强机动目标的精确跟踪。将修正因子设为

μ(k)=exp(g(k)/g(k-1))

(13)

(14)

2.2 交互式多模型

2.2.1 输入交互

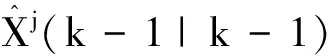
(15)

式中:

(16)

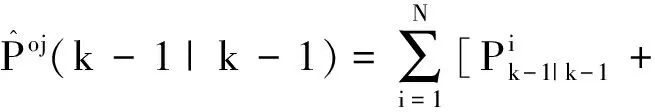
(17)

2.2.2 模型修正

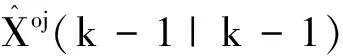
2.2.3 模型可能性计算

若模型j的滤波残差vkj，相应的协方差为Skj，并假定服从高斯分布，那么模型j的可能性为[7]

(18)

式中,

(19)

2.2.4 模型概率更新

(20)

2.2.5 输出交互

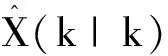
(21)

(22)

2.3 多“当前”统计模型交互

针对当前统计模型难以根据不同类型机动目标自适应的选取机动频率的问题，设置3个不同自相关时间常数的当前统计模型，机动频率分别取典型经验值，α1=1/60，α2=1/20，α3=0。α3=0即为匀加速模型，是为了弥补“当前”统计模型对弱机动和非机动目标精度低的不足而设定的，然后将这3个子模型代入交互多模型算法中，形成多“当前”统计模型交互算法。3个模型的初始概率分别为0.3、0.4、0.3，模型转移矩阵

3 仿真结果

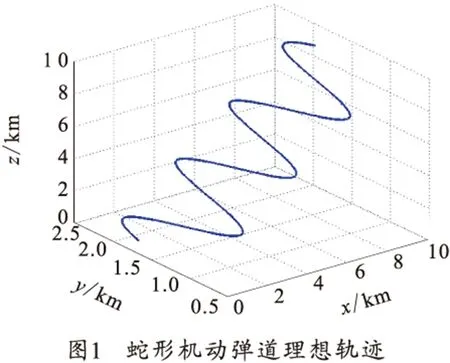
在蛇形机动弹道理想轨迹基础上叠加测量噪声，假定激光测距、红外测角的测量噪声均为高斯白噪声，噪声方差σR=5 m，σβ=1 mrad，σε=1 mrad，仿真次数为200次。

分别采用匀加速模型算法(CA-KF)、标准“当前”统计模型算法(CS-KF)和笔者提出的交互式多“当前”统计模型算法(ACS-IMMKF)对量测弹迹做200次蒙特卡洛仿真。图2为3种算法滤波后轨迹水平面投影对比图，从图中可以看出，ACS-IMMKF算法的滤波轨迹最接近理想航迹。图3～5为3种算法的位置滤波估计均方根误差曲线，表1为均方根误差平均值。

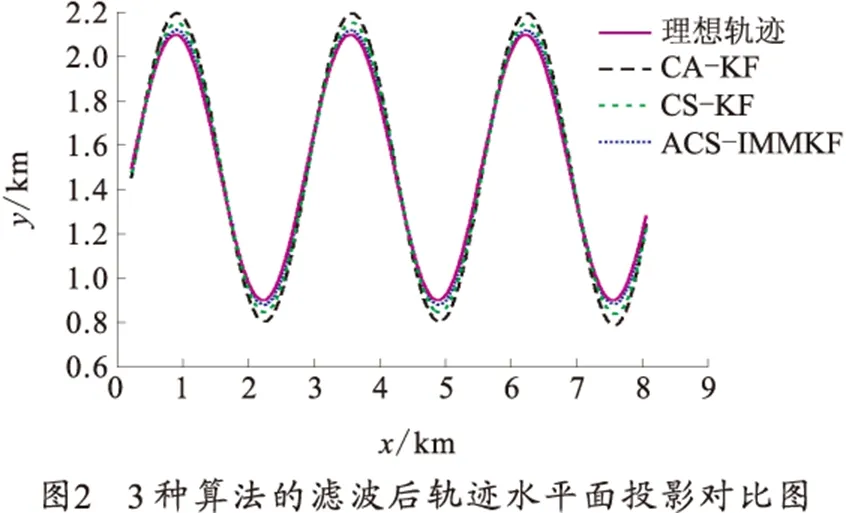
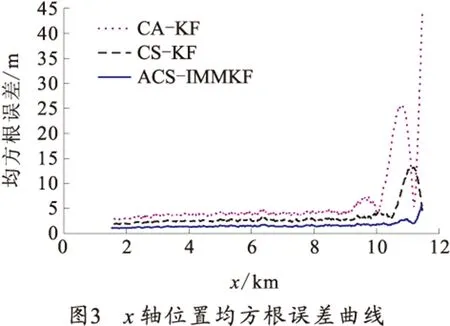
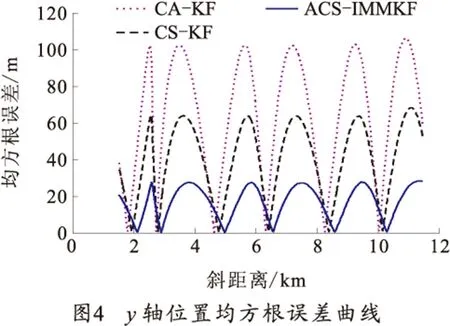
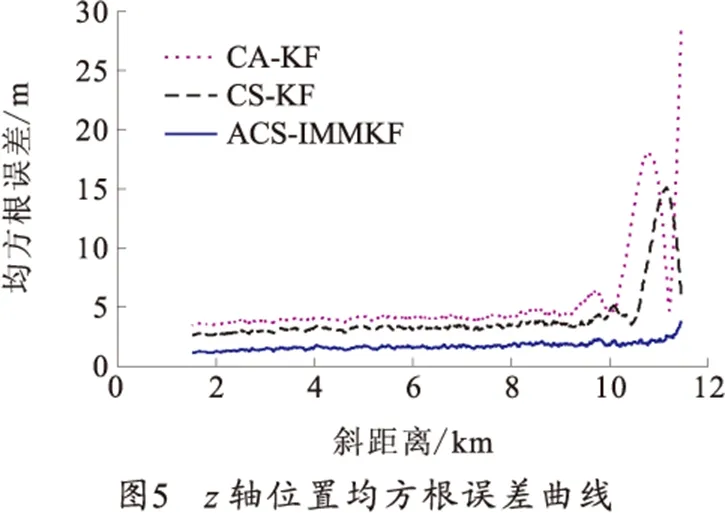
表1 3种算法的位置误差平均值统计表

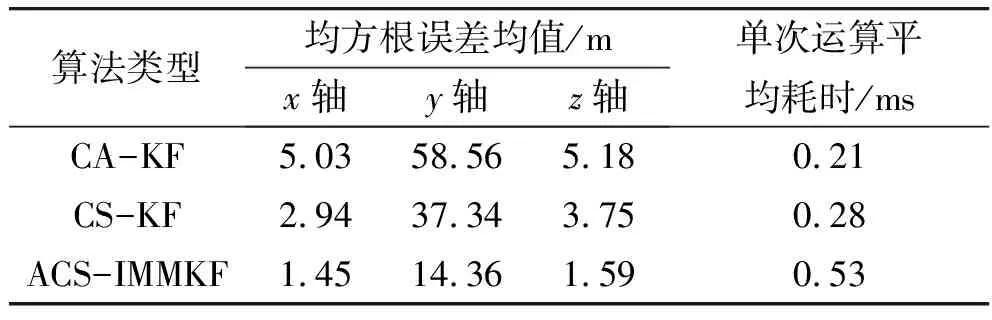
算法类型均方根误差均值/mx轴y轴z轴单次运算平均耗时/msCA-KF5.0358.565.180.21CS-KF2.9437.343.750.28ACS-IMMKF1.4514.361.590.53

从仿真结果可以看出：

1)目标在x轴和z轴方向上处于弱机动状态，3种算法跟踪效果都比较理想，都没有出现较大偏差，ACS-IMMKF算法的滤波精度相对较高，收敛速度比较快。

3)ACS-IMMKF模型算法相对于另外两种算法在转弯处的均方根误差峰值最小，而且收敛速度最快，滤波精度高于其他两种算法，这是由于ACS-IMMKF选取了不同机动程度的CS模型相互交互，该算法可在滤波过程中根据新息的变化自动修正加速度极限值调节滤波增益，快速响应目标转弯机动。

4)与另外两种算法相比，ACS-IMMKF模型算法在相同条件下的单次计算耗时偏大，但没有超过1 ms，计算量适中。

4 结束语

针对巡航导弹类目标跟踪问题，笔者提出了一种交互式“当前”统计多模型算法。仿真测试结果表明，该算法跟踪精度高，实时性好，因此比较适合在制导弹药类目标跟踪中应用。需要指出的是，算法中的“当前”模型机动频率α取的是典型经验值，如何能在滤波过程中对机动频率α进行自适应调整以适应不同类型的目标，将是下一步重点研究工作。另外，笔者采用的多模型算法是基于固定结构的，计算量相对较大，后续工作可对变结构多模型VSMM算法开展研究，提高运算实时性，减少模型间不必要的竞争。