基于马尔科夫的装备状态维修决策模型
2018-10-08徐廷学张加平李志强
徐廷学,安 进,张加平,李志强
(海军航空工程学院 兵器科学与技术系,山东 烟台 264001)
传统的维修检测是以“浴盆曲线”理论为基础,采取定时维修及经验分析法相结合对装备进行维修保障,在维修过程中,易造成“过维修”或“欠维修”问题[1]。基于状态的维修自上世纪70年代出现并逐步发展,是一种较新的装备维修方式[1],是在获取装备状态检测、故障诊断、维修统计等数据信息的基础上,经过一系列的判断处理,判断装备在检测时所处的状态,预测装备接下来的发展变化趋势,根据装备维修需求采取有针对性的维修,使得维修工作更加及时、准确,同时,能尽可能地节省维修经费。
随着基于状态维修的方法不断发展,各国在基于状态的故障诊断、预测等方面都有了较大的进步。学者Conroy等[2]设计了一种可进行故障诊断的专家系统以实现基于状态维修决策;Tomita等[3]提出了一种基于振动量的基于状态维修决策方法;之后,文献[4]中提出基于状态维修决策标准化的4个准则。目前,在武器装备的维修保障过程中,基于状态维修决策理论和技术得到了更加广泛的应用,在俄军和美军的应用中,研究周期得以缩短,成本消耗得以减少,装备维修的成本效益得以极大提高[5]。
基于状态维修决策在我国虽然技术起步晚但发展快。董玉亮等[6]提出基于决策树的证据推理方法,将故障诊断、实验中获得的定量知识与维修人员依靠经验获得的定性知识相结合,实现汽轮机组的状态评估;赵文邦等[7]提出基于云理论的状态预测方法,利用装备的历史状态信息与当前状态信息构造综合云,在某型发动机上进行了状态的动态预测。而在军用方面,基于状态维修决策方法也逐步得到重视,张仕新等[8]基于威布尔比例风险模型,研究了不同的时间间隔下的状态维修,得到一个综合性的评价决策结果;信燕杰等[9]搭建基于非理想维修的状态维修决策模型,探讨随着装备维修次数的提高,可靠性提高规律如何,对维修所采用的维修方式进行优化,提高装备的可用性。以上研究在各领域针对不同设备进行维修决策,取得了一定成果,但在对状态的动态掌握、状态转移与实际状态的关联以及对实际维修工作的指导上还有待进一步研究讨论。
笔者在以上研究的基础上,运用动态马尔科夫理论,选取装备关键部件,利用历史信息和统计数据获取装备实际状态及其公式和转移概率,进而对状态和维修时间进行预测,从而实现维修优化,为决策提供指导。
1 马尔科夫链及其应用分析
1.1 传统状态维修决策
一般情况下,装备的维修保障方式以定期检测的方式为主,其主要的基础理论是P-F间隔期,通过定时的检测确定装备的潜在故障发生的时刻,并采取提前维修或者是等待装备发生故障后维修等方式进行保障,从而避免装备状态变坏产生的不利影响[10-11]。其中,为确保装备维修的及时有效,净剩P-F间隔期应大于装备的停机时间(即从发现潜在故障到装备停机所需的最大时间)。
这种传统的经验分析法极易出现“维修过度”或“维修不足”的现象,使得装备的经济性降低、影响装备功能的发挥,影响装备的作战效能;另一方面,当故障发生时,无法将故障定位到具体的单元,拖慢了维修保障的速率,易造成严重后果。
1.2 基于马尔科夫的动态状态维修决策建模
基于马尔科夫的状态维修决策方式,首先对被测对象进行状态检测,获取状态信息特征量,综合装备的历史状态信息及维修信息等多方面信息分析装备现阶段的状态,判断出装备此时所处的状态区间及等级,并通过马尔科夫链的转移模型及转移矩阵计算装备产生故障的时间及概率,确定出预防性维修时间,在这种预测方式下的维修预测结果,为下一步装备的维修保障工作提供必要的技术指导。
引入马尔科夫链来搭建基于状态的维修决策方式,改变传统的定期维修固定的维修时间差,预见性地提出维修间隔,提高维修经济性的同时,保证装备的正常发挥功能。
选取装备的n个技术状态,分别记为C1,C2,…,Cn(其中C1为装备最初的技术状态,即装备启用时的技术状态;Cn为装备到达可靠寿命时所对应的技术状态),状态D表示装备处于故障状态,也可看作是装备的第n+1个技术状态。
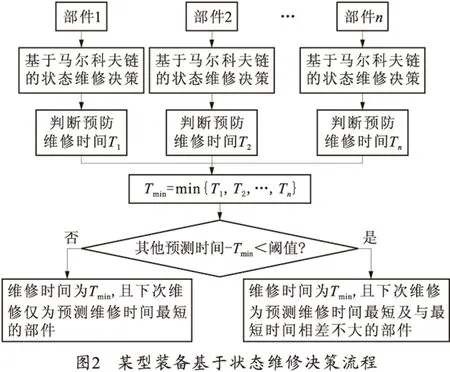
由于装备状态总是由较好的技术状态转变向较差的技术状态,是一个渐变且不可逆转的变化过程(除非人为的进行维修干预),所以装备的技术状态转变是一种非常返态的技术状态转变。假定i 引入马尔科夫链来对装备进行故障预测: 若装备测试时位于的状态为Ci,对应的时间为ti。若此时装备要进入故障状态,则可能经历的装备技术状态包括Ci,Ci+1,…,Cn。而故障状态D为吸收态。那么,装备从某一固定的状态Ci转移到发生故障的状态D的时间预测问题可转化为:装备从状态Ci转移到状态Ci+1,…,Cn的时间即停留时间的总和问题。 假定装备状态转移矩阵为P,用P(i,j)=Pij表示位置(i,j)上的元素。将装备的状态矩阵P进行转置,可以得到 (1) 式中:Q是指装备的状态转移矩阵P除去故障状态D后转置所得;Q中的状态均为非故障状态[12]。 令Yj表示装备在状态转移过程中经过非故障状态Cj的次数,则有 (2) 则矩阵I+Q+Q2+Q3+…在(i,j)位置的元素为 E(Yj|X0=Ci)= (3) 式中,Pn(i,j)表示从某一状态i出发,经过了n次的状态转移后,处于给定的状态j的概率。 令M=(I-Q)-1,由矩阵的性质可知,M=(I-Q)-1=I+Q+Q2+Q3+…,则M在(i,j)位置上的元素Mij代表了从状态Ci开始,访问状态Cj的平均次数。 (4) 即当装备的初始状态为Ci时,装备经过状态转移到达装备的故障状态D所需要的最短平均步数。如果装备在各个技术状态的停留时间能够提前得知,那么便可以推算出装备到达故障状态D所需要的时间。 采用马尔科夫链的方式对某型装备进行状态维修决策,首先假定装备部件的故障和维修过程是相互独立的,彼此之间没有相互联系[13]。由于装备的储存环境相对固定,所以状态的判断以维修次数和使用时间为主,主要依据维修次数进行经验判断。维修决策模型如图2所示。 根据上面的流程图可以看出,在进行装备维修决策时,首先对待维修决策的关键部件进行划分,设定彼此间的维修决策互不影响,并对每一个部件进行维修决策,对每个部件得出维修决策结果,得出相应的维修时间。进一步选出维修时间的最小值为基础,逐一作差,得出相应的时间差,若时间差大于阈值,则在下一次的计划维修时忽略维修时间较长部件的维修,各部件进行分次维修;若两者间的时间差较小,则将两个部件的维修归为一次维修中,以减少维修的次数过多对装备本身状态可靠性的影响。 根据上面的分析可以看出,影响某型装备各部件状态的因素主要是维修次数n以及维修后使用时间t,而某型装备的储存环境以及维修人员的技术水平可以暂时忽略不计。 对某型装备关键部件进行编号q=1,2,…,n,同时设定: 1)获取状态判断数据函数:f=f(t,n) 2)判断数据状态函数:h=h(f) 3)转移矩阵函数:Q=Q(h) 则某部件q故障预测时间为 (5) 维修决策时间函数: Tmin=min(Tq)=min(T1,T2,…,Tn) (6) 维修时间差函数:ΔTq=Tq-Tmin 基于状态维修决策过程中,根据状态影响因素维修次数和维修后使用时间,获得状态数据,并根据状态数据确定此刻装备所处的状态等级,列出状态转移矩阵,计算状态转移概率,进一步计算出单个装备部件预防性维修时间,通过求解最小值以及各维修时间与最小值的差值,并与设定的时间差阈值进行比较,做出相应的维修决策。 以某型装备关键部件1和部件2的维修决策为例进行分析。依据装备储存环境条件,部件1和部件2的维修次数以及使用时间,将部件1和部件2分为良好、正常、劣化和拟故障4种状态[1],分别表示为B1,B2,B3,B4以及C1,C2,C3,C4以及故障状态D。 对部件状态的评估主要依据使用时间t和维修次数n。根据部件历史故障和维修检测信息,经数据分析拟合计算以及专家意见可得,部件1的影响因素相关函数表达式为 (7) 部件2的影响因素相关函数表达式为 (8) 部件1的状态判断如表1所示。 表1 部件1状态判断表 部件2的状态判断如表2所示。 表2 部件2状态判断表 若经查询得部件1的维修次数n=0,维修后使用时间t=50 d,部件2的维修次数n=0,维修后使用时间t=300 d,即判断部件1的状态为B1,部件2的状态为C3,分别计算两部件的状态预测维修时间,以部件1为例,部件1各状态停留时间如表3所示。 表3 部件1各状态停留时间表 根据历史信息计算得,部件1的转移概率如表4所示。 表4 部件1转移概率表 同理,可以查得部件1处于其他状态时的状态转移概率,并列出状态转移矩阵, 建立马尔科夫链如图3所示。 进一步计算转换矩阵,得: 计算部件1处于此状态时的预测维修时间得:T1=1.515 1×250+1.082 3×150+0.974 0×60+3.003 2×40≈720 d 同理,可以计算部件2的预测维修时间为T2≈287 d。 那么两者的预测维修时间差为ΔT=433 d,两者的时间差较长,所以在下次预防性维修时,可以只先考虑部件2,而无需对部件1进行预防性维修。 若经查询得部件1的维修次数n=1,维修后使用时间为t=300 d,部件2的维修次数为n=0,维修后使用时间为t=300 d,即两者的状态分别处于B3与C3状态,通过马尔科夫链预测可得两者的预防性预测维修时间分别为T1=222 d与T2=287 d,两者的预测维修时间差为ΔT=65 d,两者的预防性维修时间相差较小,所以在下次预防性维修时,应对部件1和部件2同时进行预防性维修,以减少对某型装备的维修性维修次数,减小因维修次数过多对装备本身可靠性的影响。 笔者通过将马尔科夫链的状态转移与某型装备的技术功能状态间的转移相结合,完成了引入马尔科夫链为基础的基于状态的动态维修决策模型的搭建,改变传统的维修决策固定维修间隔时间的方式,实现对维修时间的有效控制,结合维修时间的相关性以及维修时机的相关性,对装备的维修最佳时间间隔做出判断,减小对装备本身固有性能的影响。在后续研究中,可进一步考虑环境条件与维修保障人员的技术水平的影响因子,使决策更加准确有效。
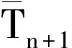
1.3 某型装备基于状态维修决策流程
2 实例分析
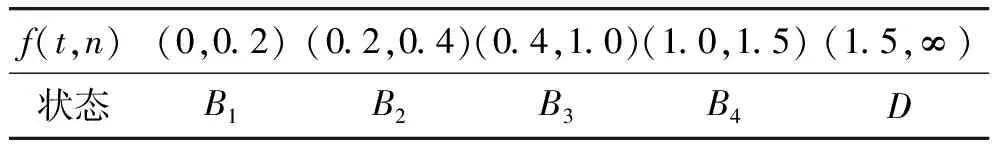





3 结束语
