基于蒙特卡洛模拟信息不完全下双寡头垄断市场动态研究

【摘 要】在微观经济学中，分析双寡头垄断市场的产量决策时，假设双方都已知自己和对方的成本函数，都知道市场的需求函数的前提下，可以达到古诺纳什均衡产量，但现实社会中一方是很难知道对方的成本函数的，本文就是在放宽这个假设的条件下，用水晶球软件的蒙特卡洛模拟功能来说明是否还会达到古诺纳什均衡。

【关键词】双寡头垄断；成本函数；古诺纳什均衡；蒙特卡洛模拟

一、双寡头垄断市场的古诺纳什均衡

古诺模型是早期的寡头模型，它是由法国经济学家古诺在1838年最先提出的。古诺模型是一个只有两个寡头厂商的简单模型，因此该模型也被称为“双寡头模型”。微观经济学中，双寡头垄断市场是分析两家寡头垄断厂商生产—种相同的产品时在寡头垄断市场中的行为。这一寡头垄断模型假定：每家厂商都不会力求去控制或有意地算计对方，或者说，寡头垄断厂商在追求自身的利润最大化时，都将作为其竞争者的寡头垄断厂商的产量看作是不受自己产量决策影响的。两个寡头经过博弈形成的均衡为古诺均衡，也叫古诺纳什均衡。

王礼刚、杨红（2005）对比完全信息和不完全信息的静态古诺均衡，认为古诺均衡介于，双方合谋的沟通均衡和完全竞争市场条件下的竞争均衡之间。

张旭平、林勇（2010）利用博弈论分析了完全信息条件下静态古诺模型，得出纳什均衡时产量和利润，认为如果两个厂商合谋，联合决定产量，比双方只考虑自身利益做出决策而得到的利润要高。并利用博弈论中囚徒困境分析了双方只要是考虑自身利润最大化，就不会选择合谋，而达到古诺纳什均衡。接下来对不完全信息古诺模型进行分析，假设：两寡头进行同时决策的产量竞争，市场需求为市场总产量线性函数，厂商A的成本函数为正比例函数即无固定成本，边际成本固定，这是两厂商的共同知识。而厂商B的成本函数为正比例函数，有两种可能的情况：一种是高产量，一种是低产量，厂商B自己知道实际是哪一种，厂商A只知道两种情况的概率。对这个静态贝叶斯博弈作分析，得到这个博弈的贝叶斯—纳什均衡的产量和利润，并对比完全信息条件下古诺纳什均衡的产量。最后对完全信息古诺模型做了无限次数博弈，即动态分析，认为双方仍然会陷入囚徒困境，最终采取静态下古诺模型的产量。

在现实社会里，由于信息不完全，一方只可能知道自己的成本函數，假设市场的需求函数是公开的信息，那么它就可以知道自己的利润函数，但通常是不可能知道对方的利润函数的，所以他只能根据对方的本期的产量来对自己下次的产量进行决策，同样的对方也会是这样决策，那么在这个假设条件下双方动态调整会达到古诺纳什均衡吗？如果双方恰好在第一期各自选择了其古诺纳什均衡的产量，很显然在第二期及之后他们会一直均衡在这个最优产量水平下，但是如果他们初期没有恰好选择了其古诺纳什均衡产量，那么经过几期的动态调整会出现古诺纳什均衡吗？这就是我们本文要考虑的问题。

二、蒙特卡洛模拟

蒙特卡洛（Monte Carlo），又称随机抽样或统计试验，属于计算数学的一个分支，它是在二十世纪四十年代中期发展起来的。蒙特卡洛方法能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。这是以概率和统计理论方法为基础的一种计算方法，将所求解的问题同一定的概率分布相联系，使用随机数（或更常见的伪随机数），用电子计算机实现统计模拟或抽样，以获得问题的近似解，来解决很多计算问题的方法。

当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，可以通过试验的方法，得到这种事件出现的频率分布，或者这个随机变量的平均值，并用作为问题的解，这就是蒙特卡洛方法的基本思想。蒙特卡洛方法，利用数学方法来加以模拟，即进行一种数字模拟实验。它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。蒙特卡洛方法主要有三个主要步骤：构造或描述概率过程；从已知概率分布抽样；得出各种估计量的概率分布。本文的蒙特卡洛模拟是借助于安装在Microsoft excel软件上的水晶球软件实现。

三、信息不完全下双寡头垄断市场蒙特卡洛模拟

本文是在信息不完全条件下，双寡头垄断市场中的两个寡头仅仅知道自己的成本函数，而不知道对方的成本函数，并且成本函数为更接近实际情况边际成本递增的二阶非线性函数，双方都是在一定的产量范围内，随机进行第一期的决策，在动态条件下分析二者的产量动态变动。

双寡头垄断市场中有两个供应者，他们的产量取决于对方的产量，双方的产量共同供给消费者。为了下一步的蒙特卡洛模拟，现在假设两个供应者为A寡头和B寡头（下面简称A、B），市场的需求函数是P（Y1，Y2）=60-Y1-Y2，其中P是市场价格，Y1和Y2分别是A和B的产量；A和B的成本函数分别是C（Y 1）=Y 12和C（Y 2）=15Y 2+Y 22，他们的利润函数分别是π1=PY 1-C1=（60-Y1-Y2）×Y1-Y12和π2=PY2-C2=（60-Y1-Y2）*Y2-15Y2-Y22，其中π1和π2分别表示A和B利润。

首先看完全信息下静态古诺纳什均衡的情况。

接下来看信息不完全下双寡头垄断市场的蒙特卡洛模拟情况。

首先在excel电子表格中建立该经济模型，然后利用水晶球软件定义双方的第一期产量为假设单元格，产生随机数，进行蒙特卡洛模拟。定义双方随后若干期的产量为预测单元格，最后分析模拟结果。

首先在excel电子表格中建立模型，除第一期外，A的当期的产量取决于B的上期产量，B的当期产量取决于A的上期产量，如此进行20期生产，并且第一期我们假定双方的产量是随机的，由市场的需求函数可知，Y 1的定义域是[0，60]，所以假设A的第一期产量服从在[0，60]里的均匀分布，同样的假设B的第一期产量也是服从在[0，60]里的均匀分布。我们利用水晶球软件，将第1期的A，B的产量都定义为[0，60]里服从均匀分布的假设单元格，把双方第3期，第5期，第10期和第20期的产量，定义为预测单元格，然后进行5000次的随机模拟，观察预测单元格的统计变量。关于20期的选定，结合后面模拟结果统计数据可以知道期数已经足够长，没有必要再做更多期的模拟。关于5000次随机模拟选取，如果A和B的产量为整数，那么在0到60中，双方各有61种选择，可以组合出61×61= 3721种组合，5000次模拟差不多可以覆盖各种组合情况。

如图1，在excel中，列B表示A寡头，列C表示B寡头，行表示第几期的生产，从单元格B2到C21表示相应的产量，在单元格B2，C2中任意输入两个符合定义域的数（注，由水晶球软件和蒙特卡洛模拟的特性，输入任何定义域之内的数字都不会对结果有影响的。）如B2为20，C2为30。在单元格B3中输入公式“=15-C2/4”相当于A寡头的反应函数Y1=15-Y2/4，同样的，在单元格C3中输入“=（45-B2）/4”相当于B寡头的反应函数Y2=（45-Y1）/4，以次类推，在单元格B21中输入“=15-C20/4”，在单元格C21中输入“=（45-B20）/4”。接下来，用水晶球软件的Define Assumption键来定义假设单元格B2，如图2，定义为[0，60]的均匀分布，同样的C2定义为[0，60] 的均匀分布。再用水晶球软件中的Define Forecast键来定义B4单元格为预测单元格，名称为A寡头第3期产量，C4为B寡头第3期产量，同样定义单元格B6，C6，B11，C11，B21和C21为预测单元格，并定义相应的名称。

在设置好模拟的参数后，就可以用水晶球软件开始进行蒙特卡洛模拟了。本文将模拟次数设置成5000次，其他模拟参数均为软件的默认设置。5000次模拟后出现如下结果，两个寡头第3期和第5期的产量分布用图3至图6模拟结果的频率频数轮廓图来描述，第10期和第20期的产量情况用表1模拟结果的统计量图来描述

图3和图4，图中横坐标为产量，左侧纵坐标为相应产量的概率，右側纵坐标为频数，我们可以看出，在第3期的时候，A寡头的产量已经集中在12.23到15.93之间了，B寡头集中在7.53到11.23之间了，都比双方初始的区间[0，60]集中了很多，并且明显有向着各自的古诺纳什均衡点集中的趋势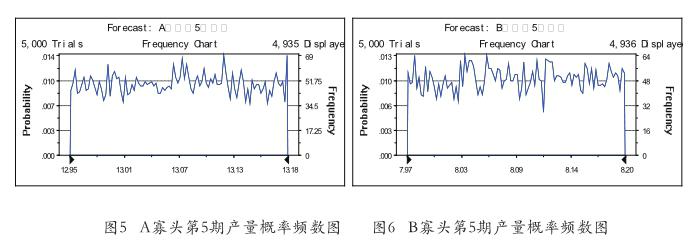

如图5和图6，看第5期的产量图，A寡头的产量已经集中在12.95到13.18之间了，B寡头集中在7.97到8.20之间了，A和B的产量均比第3期的产量有进一步向着古诺纳什均衡点集中的趋势。

到了第10期，如表1，看A寡头第10期的产量的统计数据，A寡头的产量的平均值和中值为13.00，方差标准差为0，最大值和最小值都是13.00，注意到众数是不存在的，这些统计数据表明A寡头的产量已经非常接近于其古诺纳什均衡产量13.00了，但还不准确为13.00，这里面的方差标准差为0，最大值最小值都是13.00应该是非常近似的值，否则众数应该是存在的。同样由B寡头产量的统计数据也可知B寡头的产量已经非常接近于其古诺纳什均衡产量8.00了，但还不确切为8.00。

到了第20期，看A寡头第20期的产量统计数据，平均值和中值为13.00，方差标准差为0，最大值最小值都是13.00，同时众数也是13.00，这些统计指标已经确切表明A寡头的产量已经等于其古诺纳什均衡产量13.00了。同样的，第20期B寡头的产量也等于其古诺纳什均衡产量8.00了。由双方的反应函数可知，第21期双方的产量将和第20期的产量完全相同，也就是说，在其他情况都不变的条件下，A和B的产量就继续稳定在他们的古诺纳什均衡产量组合（13.00，8.00）了。

四、结论

经过对水晶球5000次蒙特卡洛模拟的结果分析，在双寡头垄断市场条件下，两寡头已知市场需求函数，自己的成本函数和利润函数的前提下，在不知道对方的成本函数和利润函数信息不完全的情况下，经双方多期（本文可以认为至多经过20期）按照自己的反应函数进行动态产量调整，最终还是会均衡在双方都知道对方成本函数和利润函数，完全信息静态条件下得到的古诺纳什均衡产量的。

（浙江广厦建设职业技术学院，浙江东阳 322100）

参考文献：

[1][美]哈尔R.范里安 著，费方域、朱保华等译微观经济学：现代观点[M]，格致出版社 上海三联书店 上海人民出版社，2015（3）

[2]李传志，杨光.不完全信息的古诺模型分析[J].山西财经大学学报，2007， 29（2）.

[3]曹承龙，朱晓玲 基于不完全成本信息的网约车平台公司运营策略博弈分析 [J] 五邑大学学报（自然科学版），2017（5）

[4]张旭平林勇 古诺模型的演化分析[J]，北方经济，2010（2）

[5]王礼刚，杨红.完全信息与不完全信息下的古诺模型之比较[J].西北民族学报（自然科学版），2005（12）

[6]王巧 古诺博弈模型中的理性假设问题[J]，科技视野2014（12）9，23

作者简介：刘曌（1975 —），男，黑龙江牡丹江人，浙江广厦建设职业技术学院经外学院讲师，硕士，主要从事商业经济 应用经济学研究。