利用Tracker研究气垫导轨上弹簧振子运动

史振宇 丁益民 张余梦 殷子棋 蒋富丽

(湖北大学物理与电子科学学院,湖北 武汉 430062)

Tracker是国外针对物理教学而开发的视频跟踪分析和建模工具软件，可以手动或自动跟踪对象的位置、速度和加速度等并动态显示[1]。气垫导轨上的弹簧振子运动可以看作水平方向无摩擦的直线运动，在弹簧质量不能忽略的情况下,在气垫导轨上研究弹簧振子的简谐运动，将弹簧本身的动能考虑在内，可以来研究短时间内弹簧振子系统运动中的机械能守恒问题[2]。而对于系统中长时间的运动必然要考虑黏滞阻力的存在,一般阻尼系数的计算可从品质因数的角度推算,当阻尼很小时，采用最大速度衰减法的近似求得气垫导轨的阻尼系数较为准确方便[3]。本文通过录制气垫导轨上弹簧振子从简谐运动到阻尼振动全过程的运动视频,分不同时间段利用Tracker软件较为准确地追踪气垫导轨上弹簧振子运动中的位置，并得到其运动的相关数据。在此基础上,通过建立坐标轴、定标杆，结合形象直观的图像、表格进行定量分析。研究短时间段弹簧振子运动图像,验证弹簧振子系统中的机械能守恒,并对长时间段的弹簧振子运动图像进行函数拟合,研究其做阻尼振动的运动规律,并计算滑块在气垫导轨上运动中的阻尼系数。

1 实验原理

气垫导轨上弹簧振子的简谐振动原理图如图1所示。两弹簧l1,l2的劲度系数分别为k1=1.592N/m、k2=1.767N/m；质量分别为m1=0.0075kg、m2=0.0075kg；滑块质量为M=0.2300kg。

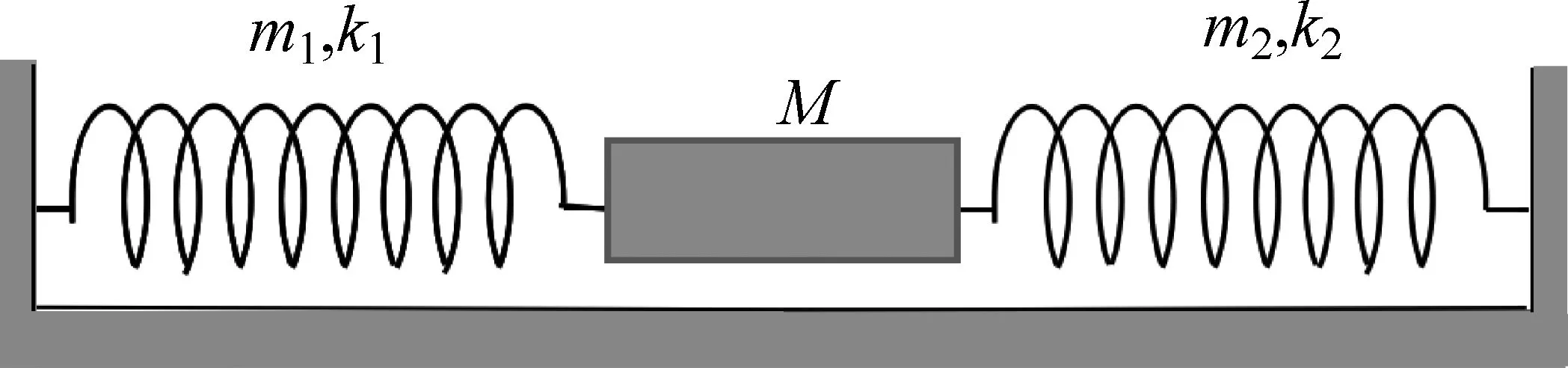
图1 气垫导轨简谐振动示意图

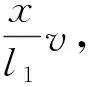
(1)

(2)

对式(1)积分得

(3)

(4)

整个系统动能与势能之和为

(5)

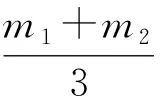
(6)

当滑块在平衡位置时,弹簧l1、l2伸长后长度分别为x1=0.569m、x2=0.529m,以滑块在平衡位置处为原点，滑块位置为x时，Δx1=x1+x、Δx2=x2-x.令滑块在不同位置的机械能为E0、E1、E2、E3、E4、…,前后位置机械能的差为

ΔE=En-1-En(n=1,2,3,…)

(7)

当ΔE=0时，系统机械能守恒，考虑到气垫导轨上的阻力的影响，ΔE不可能为零，但ΔE越小，说明系统能量损失越小，实验结果越精确。

2 实验操作

(1) 实验准备。下载安装Tracker软件，按图1安装好实验设备，固定好拍摄设备(手机或普通数码相机均可)，视频帧率为25帧以上即可得到较好的效果。

(2) 拍摄视频。为了方便捕捉滑块的运动，在滑块中心部位贴上边长为2cm的白色方块纸片作为质点对象。将滑块移离平衡位置后释放，让滑块开始运动，拍摄视频。

(3) 导入并分析视频。将拍摄的视频导入Tracker,建立适当的坐标轴，选取合适的参照物确定定标杆长度，本实验以滑块自身为参照物，设置定标杆长度为0.16m。创建一个质点，在视频中确定好质点对象，点击搜索，软件将自动搜索质点对象运动中的位置，并描绘相应的图像。图2为Tracker导出的滑块x-t图像,右侧为相应的数据。

图2 滑块的位移(x)-时间(t)图像

3 数据处理及分析

分析图2可以得出，在将近5个周期内，系统的最大振幅基本相等，而在最大振幅处滑块的速度为零，则此时系统的动能与势能之和等于势能大小，且系统的机械能趋近相等。为了更好地验证系统的机械能守恒，利用Tracker分析得到滑块运动的v-x图像如图3所示。

在经历了这样特殊的课程之后，从新加坡中学走出来的学生具有非常敏锐的“批判性思维”和“辩证思维”，他们的逻辑思维能力快速成长，也同样对于他们的学术课程大有助益。

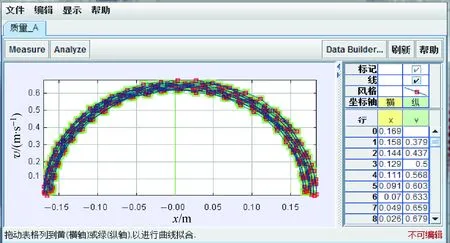
图3 滑块的速度(v)-位移(x)图像

从图3中选取5个点，记录质点对象位置x与速度v，将选取的5组数据代入式(6)计算系统总的机械能，并按式(7)计算两点之间的机械能损失量ΔE。取图3第一行数据x0=0.158m,v0=0.379m·s-1为初始状态，代入式(6)计算初始状态的机械能E0得E0=0.559J。

表1 取5个点计算所得实验数据

在数据表格中，每10行记录的数据时间间隔为0.333s。从实验结果可以看出，系统的振动在相邻的几个周期内损失的机械能ΔE非常小，可以近视看作总机械能守恒的简谐运动。但时间间隔越大时，机械能损失也越大。

由于阻力不可避免，随着时间的推移，系统的机械能也随之减小，为了完整地研究这种振动，可利用Tracker记录较长时间的振动图像，进一步分析系统的阻尼系数。图4是Tracker记录滑块运动2分钟的x-t图像。随时间的增加，滑块运动的最大振幅明显减小，说明系统在长时间的运动过程中有较为明显的机械能损失。

图4 滑块的位移(x)-时间(t)图像

若考虑气垫导轨上的粘滞阻力，

Ff=-bv

(8)

其与滑块运动的速度成正比，b为阻尼系数。

-(k1+k2)x-bv=Ma+m0a

(9)

(10)

令M+m0=M0,式(10)可写为

(11)

其解为

x=Ae-β tsin(ωdt+θ)

(12)

可得

(13)

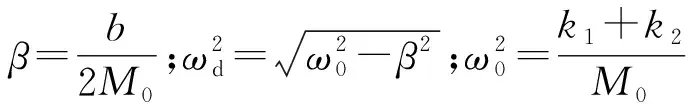
对式(12)求导得

v=Ae-β t(-β)sin(ωdt+θ)+Ae-β tcos(ωdt+θ)ωd

(14)

将式(13)代入式(14)得

(15)

当x=0时，滑块处于平衡位置

v=ωdAe-β t

(16)

由式(16)可知在平衡位置处滑块速度关于时间呈现指数衰减。利用Tracker分析得到滑块的v-t图，在平衡位置处，滑块的最大速度随时间的衰减如图5所示。

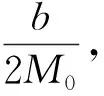
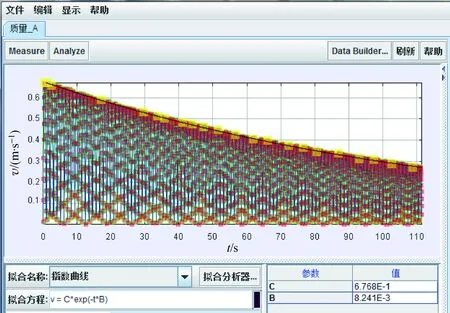
图5 滑块的速度(v)-时间(t)图像

4 结语

综上所述，气垫导轨上的弹簧振子运动在短时间内机械能损失极小，可以近似地看作机械能守恒的简谐振动。但对于其长时间的运动，必需要考虑气垫导轨上阻尼的存在。利用Tracker软件对气垫导轨上弹簧振子运动进行分析，可以精确记录气垫导轨上滑块运动的轨迹，并直接对其运动数据进行采样，且数据量大，方便选择处理。该方法方便、快捷、直观、高效，其实验结果与理论值相比误差很小，具有很高的推广价值。