一阶RC电路的深度透视： 概念、思想和方法

陈昌兆

(安徽理工大学力学与光电物理学院, 安徽 淮南 232001)

1 提出问题

一阶RC串联电路是最简单的交流电路形式，广泛存在于电磁学、电路分析、电子学、信号与系统等物理类、电工电子类课程教学中。尽管是最为简单的电路形式之一，学生们在学习过程中仍然存在不少问题，这种学习上的困难尤其表现在基于电路行为的定性分析层面上。众多的教学案例和教学研究都表明大多数学生或许能够正确地求解电路系统的微分方程，但并未完全理解隐藏于方程求解背后的核心概念和此类电路分析的总体指导思想和原则，在物理概念模糊、毫无指导思想前提下片面追求解题方法必然导致认识层面的狭隘和不足甚至是理解上的错误。

为了提高RC电路的教学效果，加深学生对储能元件电容的工作特性的深度理解，国内外的教学工作者在实际教学中尝试了很多新的教学方法并取得了不错的教学效果[1-3]。Thacker等人[4]仔细研究了美国低年级电子工程类大学生以及以色列高中生对RC直流电路中电荷和电流的认识水平，提出了一种基于微观模型的教学方法并付诸实践，通过问卷测试、面试等教学手段证明此种方法与传统的单纯求解方程的教学手段相比不仅能够从定性层面对电路行为做出正确的预测，还能够加深学生对宏观电磁现象的理解。Newburgh[5]和Osmond[6]分析一个荷电的电容器与另外一个未荷电电容器接触时电流和电荷的分布状况，将此体系类比于有活塞相连时两个不同盛水状态的水瓶体系的水流和容量分布。由美国国家自然科学基金资助的CASTLE(Capacitor-Aided System for Teaching and Learning Electricity)项目由部分高中以及大学物理教师发起，旨在通过构建基于电容的模型系统克服学生在学习电路时遇到的困难。在Steinberg和Wainwright的教学实践中，充电的电容器甚至形象地比作被压缩的空气[7]。爱尔兰都柏林城市大学的Smith教授[8]高度整合了以前关于RC电路中电容器行为的教学中对电流、电荷、电阻、电压和能量的种种唯象描述，提出了依赖于电路中电容器的状态而将电容器功能类比成导线、开关或电池，从而对电路中灯泡或电容器的定性行为作出合理判断的方法。这种方法的优势在于直观性和直接性，可以让学生在很短的时间内对RC电路的定性行为作出合理的预测。

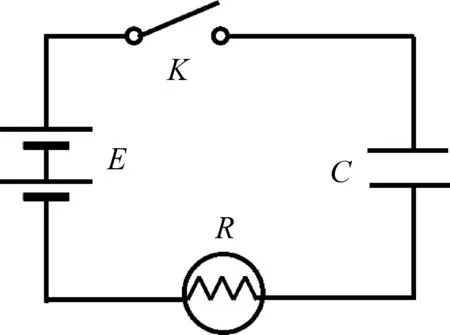
图1 由电源、开关、小灯泡和电容组成的一阶RC串联电路

实际上，采用唯象的模型系统和类比的教学方法教授RC电路固然有一定的优越性，但也存在诸多难以解决的问题。因为各种模型系统和类比对象都存在一定适用性，何种条件下采用特定的模型系统是学生很难把握的问题。单一的模型系统无法解决所有问题，而种类繁多的模型系统又会让学生变得无所适从。图1是一个由电池、电容器、小灯泡和开关组成的最简单一阶RC串联电路，假设电容器起始未充电，则从开关闭合到经过很长一段时间，问灯泡的亮度如何变化？在这一段时间跨度上，电容器的表现何时像导线，何时又像电池或开关，这些都是足以让学生困惑的问题。

纵然我们有充分理由引入电容模型讲授RC电路，模型的直观性和形象性会增强学生对电路中电容行为的感性认识，但教学本身是一个系统工程，任何感性认识最终都要理性回归。过度的依靠模型讲解问题会给学生造成先入为主的观念，模型在绝对化的同时学生的思维会僵化，这正是人类思维上的缺陷。前苏联著名实验物理学家、Nobel奖获得者卡皮查教授不厌其烦地告诉他的研究生们从事科学研究时选题的重要性，在他看来，科研好比一棵由根、枝和叶组成的大树，真正的科研应该从根上做起。教学又何尝不是这样，它同样是有层次的。教学尤其是理工科的课堂教学往往从概念(如速度、加速度、电场强度等)入手，通过实验或推理建立不同概念之间的定量关系从而获得解题的总体指导思想，这往往表现为定理或定律(如牛顿第二运动定律，高斯定理等)，最后才是具体的解题方法。概念是核心必须吃透、思想是纲领必须掌握、方法是手段作到具体问题具体分析，只有明确这一点，教师才不至于在教学过程中舍本求末，学生也不至于在学习过程中迷失方向。以下就以一阶RC串联电路的教学为例，阐述三者之间的关系和联系。

2 核心概念—电容的伏安特性

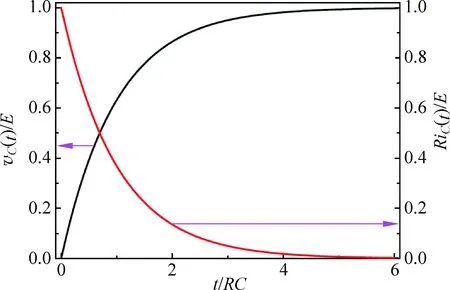
图2 开关合上后一阶RC电路中电容器上电压和回路电流随时间变化

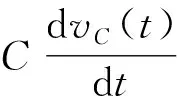
这些错误的推理反映出学生思维上混乱和物理概念上的不清晰。尽管他们给出了多种多样的错误解释，但问题的症结都聚焦于同一点，即一个物理量的时间变化率和这个物理量本身之间的关联。正如电容的伏安特性所揭示的，通过电容器的电流iC(t)正比于电容上的电压vC(t)对时间的导数，但两者不是同一个概念。开关合上时电容器上为零的电压却对应最大的电压变化率，否则电容器上的电压不会变化，又何来充放电过程。这正如力学中速度和加速度的关系，众所周知加速度是速度的时间变化率。设想一个处于静止状态的球从高处落下，t=0时刻球的速度为零但加速度不可能为零，否则球如何能下落？

学生们的困惑来自于电容器零电压时具有的最大电压变化率，单纯从数学的角度考虑，似乎是他们对瞬时斜率或者说导数的物理意义理解上有偏差。实际上，学生们的误解不仅仅是一个数学问题，还是一个哲学问题，因为它涉及对连续性、运动和无限性的错误解读。哈佛大学拓展学院的Newburgh教授把它称为芝诺悖论(Zeno’s paradoxes)的新型表现形式。[9]芝诺是古希腊哲学家，因为提出一系列关于运动的不可分性的哲学悖论而著名，其中最有代表性的就是“飞矢不动”学说。设想一支飞行的箭，在每一时刻它位于空间中的特定位置。由于时刻无持续时间，箭在每个时刻都没有时间而只能是静止的。鉴于整个运动期间只包含时刻，而每个时刻又只有静止的箭，所以芝诺断定，飞行的箭总是静止的，它不可能在运动！这显然是悖论但恰恰与学生的误解相吻合，即初始时刻电压为零，由于时刻没有间隙，所以电压不会随时间而改变。Kine[10]采用德国数学家康托(Cantor)的超穷数理论很好地解决了这一问题。康托(Cantor)的超穷数理论表明一个线段上点的数目等于超限数C，它跟线段的长度没有关系。同样的道理，一段时间间隔内瞬时时刻的数目也是独立于间隔长度的超限数C。因此，在任何一段时间间隔内都可以有无限个静止，这相当于承认了时间间隔的存在。箭在每个时刻都不动这一事实不能说明它是静止的，运动与时刻本身无关，而是与时刻间发生什么有关。除非一个物体在两个相邻的时刻处在同一位置，否则它就一定是运动的。

我们注意到前述的各种模型教学法都力图通过将电路中的电容行为与常见的生活现象进行类比从而使学生获得对电容特性的直观认识，加深对电容器上电荷分布、电压以及电容器充放电过程这些基本概念和物理规律的理解。模型教学法的使用的确在一定程度上能够提高教学效果并在众多的教学实践中得到证实，这主要得益于关于电容器的一些较为抽象的物理概念被形象化处理。但每一种模型都有自身的缺陷性，这些缺陷如果没有被学生充分地认识到就会导致错误的判断。例如，将电容器类比为储水的容器，电路中的电流被类比为水管中的水流，但荷电的电容器可以自发放电，而水流动必须在外界重力场的作用下才能实现，如何用该模型系统解释电容器的自发放电行为就存在问题。实际上，在多年的电路教学中我们发现，简单的类比教学法主要适用对象是刚刚接触电容器的入门级的学生，他们初次接触电容器并且对其工作特性知之甚少，在这种情况下引入模型系统会增强学生对电容器的感性认识，从而加深学生对基本物理概念的理解。对于有一定电路基础的学生而言，在RC电路教学中，学生们在概念体系上的最大认识误区并不是像电容、电流、电荷和电压这些物理概念的模糊不清，而在于电容的伏安特性中所蕴含的哲学困惑。教师在教学过程中必须抓住这个核心概念并引导学生走出认识上的误区，只有这样才能正确地定性分析电路并定量地求解电路。

3 基本指导思想—基尔霍夫定律

复杂的电路系统往往表现为由众多的支路、节点和回路组成的网络结构。这种网络结构的求解就不是简单的串并联电路公式所能解决的。但是电路终归是由电路元件(如电容、电感和电阻)依据一定的串并联关系连接而成的有机整体，所以电路问题的求解依据只能依靠两类约束特性。其一是元件的约束特性，它反映的是电路元件模型的关系式，上述的电容伏安特性就属于这一类。其二是网络拓扑约束，也就是由网络的拓扑结构建立的各电流和电压之间的定量关系，这种约束关系最早是由德国物理学家基尔霍夫给出，因而被称之为基尔霍夫定律。基尔霍夫定律是求解电路的普遍规律，也是进行电路分析的基本指导思想。在电磁学、电工学、电路分析以及信号与系统等课程学习中，我们或许会发现各种各样的电路求解方法，如传统的微分方程求解法、正弦稳态电路相量分析、三要素法、拉普拉斯变换法等，但没有一种求解方法不是以基尔霍夫定律为基础的。

定理或定律的讲授一般要求做到3点：首先是定理的历史渊源并从其历史渊源中找出定理成立的条件；其次是定理的证明方法或推理过程；最后才是定理的意义和应用。国内现有教材对基尔霍夫定律的描述主要放在电压、电流这些代数量正、负号的规定和解读以及应用举例上，很少涉及其来源和具体适用条件。我们在阅读过程中发现，欧美一些发达国家的高校理工科教材在介绍某个定理或定律时，会花较大篇幅放在概念或定理的引入上，如费曼的《物理学讲义》就是这样。将定理的来龙去脉以循循善诱的方式讲授给学生，并尽量以条分缕析的方法完成定理的证明或推理，这些固然需要花费较多的时间但是值得的。因为这会培养学生的探究精神，所谓知其然知其所以然，刨根问底的学习态度才是创新的源头活水，而将基尔霍夫定律直接以公式的形式抛给学生并根据公式指导学生解题是工程师的思维，不是科学家应该具有的态度。

4 RC电路分析方法

最后我们讨论一下一阶RC电路的求解方法。方法不同于概念和思想，它处于较低层面上，具有具体性和相对性。一阶RC电路的分析讨论，根据研究对象的性质和所属课程情况，分析方法有多种形式，如电磁学中常用求解微分方程，电工学中三要素法，电路分析中的正弦稳态电路相量分析法以及信号与系统中拉普拉斯变换法。还是以电路1为例，以激励信号源的电动势e(t)作为输入信号，电容器上电压vC(t)作为输出信号。对这样一个最为简单的一阶RC电路，求解微分方程、三要素法和拉普拉斯变换法是教科书中最为常见的3种求解方法，现简单分述如下。

(2) 三要素法：三要素法仅适用于直流电源驱动的只含一个动态元件的一阶电路的全响应的一般表达式。因为直流电源E驱动下，上述微分方程的定解问题其解的形式为vC(t)=vC(∞)+[vC(0+)-vC(∞)]e-t/τ，此vC(∞)=E为电容器上电压的稳态值，τ=RC为一阶RC电路的时间常数。由此可见，直流激励下一阶RC电路的全响应取决于稳态值、初态值和时间常数这3个要素，总是从初始值vC(0+)开始，按照指数规律增长或衰减到稳态值vC(∞)，响应变化的快慢取决于电路的时间常数τ。

(3) 拉普拉斯变换法：拉普拉斯变换法可以直接对(1)中的微分方程两边求拉普拉斯变换并利用拉普拉斯变化的微分性质得到RC[sVC(s)-vC(0-)]+VC(s)=E(s)，式中，VC(s)和E(s)分别为vC(t)和e(t)的单边拉普拉斯变换；vC(0-)为电容器上电压在换路前的起始值，通过积分变换化微分方程为代数方程，由此求出VC(s)并对其实施反变换即可求出vC(t)。

上述3种不同方法求解时用到的基本公式、求解过程以及适用条件等列于表1中。从表中的内容可以看出方法的多样性和具体性，追其根源，它们只不过是基尔霍夫定律在特定的激励源和电路起始状态下的变化形式，因而往往只适合于特定的场合和条件。条件变化，求解方法往往也随着变化，比如在电路分析课程学习中，我们经常用“电容上电压不会突变，通过电感的电流不会突变”来分析换路前后储能元件的初始状态的变化，但这仅限于在没有冲激电流作用于电容以及没有冲激电压作用于电感的条件成立，否则电容上电压和通过电感的电流是可以突变的。

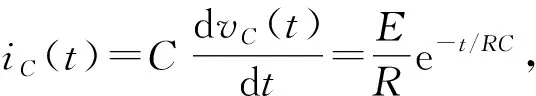
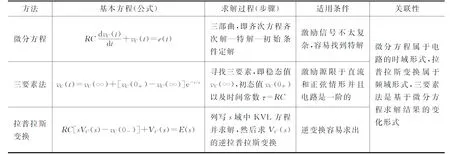
表1 RC电路常见3种电路分析方法

5 结语

一阶RC电路广泛出现在电工、电子类的课程教学中，但学生们在理解上一直有困难。多年来，国内外教学工作者为提高RC电路教学效果所作的努力大多停留在电容模型的引入和电路分析方法挖掘上，而忽略了理工科课程教学中最基本的问题：教授物理概念和思想。我们深度剖析了一阶RC电路中涉及的重要物理概念、物理学基本定律以及电路分析方法之间的层次性和主次关系，指出了学生们学习上的最大困扰植根于电容的伏安特性中所蕴含的电压变化率的认识误区以及对基尔霍夫定律作为主要指导思想的认识不足。