对称型三原子分子振动的弹簧质量模型

2018-09-29陈奎孚

物理与工程 2018年5期

陈奎孚刘霞

(中国农业大学理学院，北京 100083)

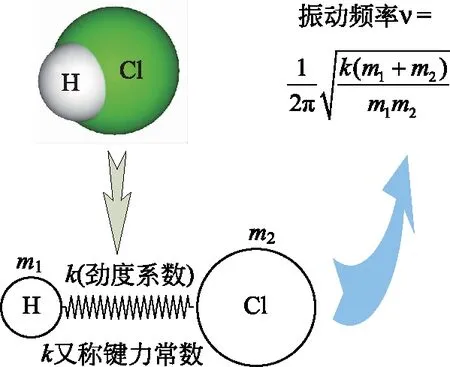
图1 双原子分子的弹簧质量模型

借助经典力学的双质量弹簧振子的振动，双原子分子的振动谱可以得到完美的解释(见图1)；三原子分子是双原子分子的自然延展，然而当前教材鲜有用弹簧振子模型来解释三原子分子振动的(尽管有期刊文献探究该命题，但似乎未被教材编写者认可)。这在认知逻辑上就会出现这样的冲突：为什么三原子分子的振动不用经典力学的振子模型来解释？况且三原子分子比双原子分子种类多得多，因此若有经典理论能解释三原子分子的，则应比仅能解释双原子分子的应用范围要大得多。论文[1-4]试图用弹簧质量振子解释三原子分子振动，但是所谈论的对象仅为直线型分子(linear molecule),比如CO2, 但H2O这样非直线型分子更普遍。另外，文[2-4]的模型不出现弯曲振动模式，但是CO2和H2O弯曲振动的频率峰在红外谱图上是确实存在的。文[1]解释了弯曲振动，但是比较牵强。为了实现弯曲振动模式，笔者在中间原子所连接的两个化学键之间添加角簧。此模型较为成功地解释了直线型三原子分子振动频率和振动模式[5]。

本文在文[5]基础上，探究对称型三原子分子的振动模型，分析其振动频率和振动模式，并用文献数据对模型进行检验。

1 振子模型

1.1 物理模型

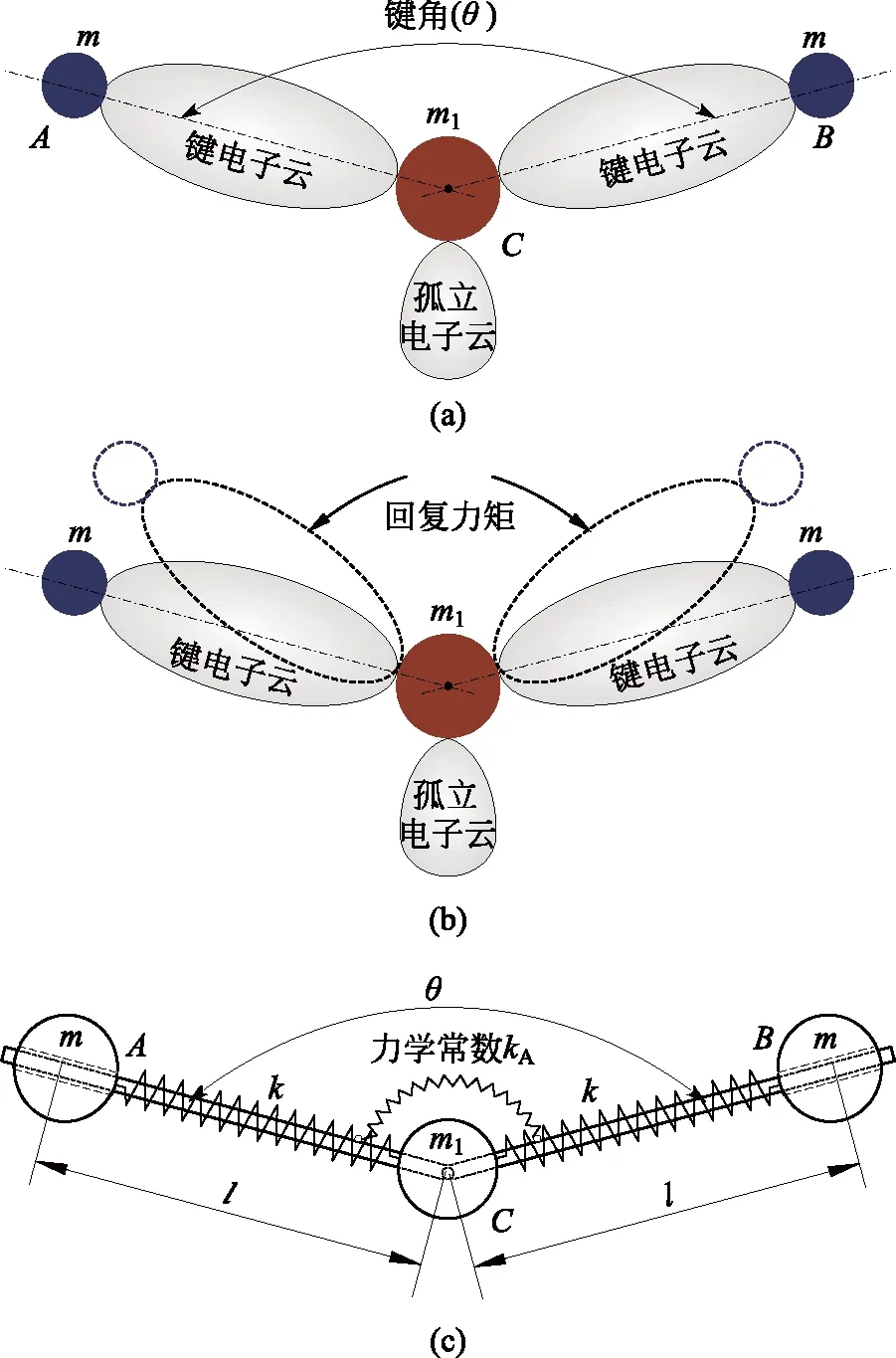
图2 三原子分子模型

三原子对称分子模型如图2(a)所示。图中：A和B是两个相同原子(简化为质点m)，C原子(简化为质点m1)在中间；两端原子A和B与中间原子通过化学键相连(两键夹角为θ)，两端原子之间无化学键；两个化学键长度和力学常数相同。为了研究振动模式，把键用线弹簧来代替。但为了体现两个键的方向，图2(c)把弹簧和质量都套在两根杆上。两杆只起示意弹簧方向的作用，它们无质量，二者铰接，并铰接到中间m1，跟随弹簧转动。

电子云的斥力试图让电子云重叠越少越好，但是除了成键电子云，中间原子的外层电子可能还有孤立电子，它也有电子云。θ是在上述电子云综合作用下保持平衡的键角，如图2(a)所示。若发生振动，键角偏离平衡值后，电子云间的斥力和中间原子对键的取向力又会把两个键推回平衡值(图2(b)所示)。图2(c)中的力学常数kA反映了这种回复力矩效果。kA的物理意义是θ改变单位弧度时，在角簧上所需施加的力偶矩。

因为三点决定一个平面，所以这3个原子质点在同一平面。对于本征振动，物体不受外力，所以对本征振动只需要考虑平面内的振动。

1.2 数学模型

图2(c)模型的3个质点在平面内运动。一个平面运动质点有两个自由度，所以整个模型有6个自由度；但是本征振动的条件是系统不受外力。在无外力的条件下，可补充3个方程：即两个动量守恒方程，一个绕质心转动的角动量守恒方程。这在数学上，模型只有3个独立的变量。综合考虑，本文选择如下3个量为广义坐标(见图3)：两个线弹簧的长度相对平衡状态的改变量ΔlA C和ΔlB C；角簧角度相对平衡状态的改变量Δθ(3个原子的6个直角坐标可由这3个广义坐标，辅以3个守恒方程唯一地表示出来; 用势能直接对应的位移量为广义坐标，与绝对的直角坐标相比，前者的物理意义更明晰一些)。

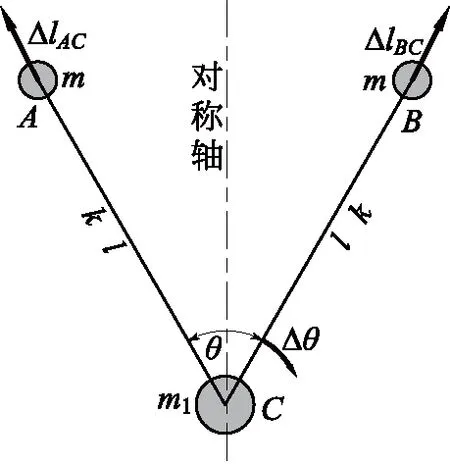
图3 分析三原子分子的广义坐标

采用上述广义坐标，模型势能非常简单，它为

(1)

式中：{Δ}={ΔlA C,ΔlB C,Δθ}为位移向量；[K]为对角刚度矩阵

(2)

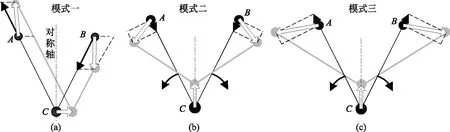
图4 振动模式

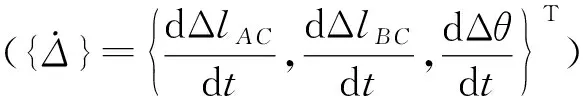
(3)

质量矩阵[M]的表达式如下

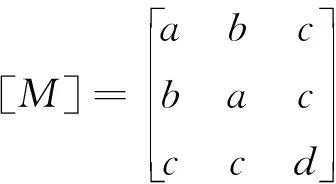
(4)

这里(下式中μ=m/m1)

(5)

利用拉格朗日方程，可建立如下振动微分方程[6]

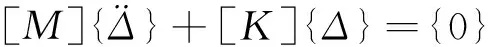
(6)

1.3 本征振动

设本征振动为{Δ}={φ}sinpt,这里p为本征振动圆频率，{φ}为振动模式。将{Δ}={φ}sinpt代入式(6)得到如下本征值问题

(-p2[M]+[K]){φ}={0}

(7)

求解式(7)得到如下3个本征频率

式中

对应式(8)和式(9) 3个本征频率的本征模式为

(10)

模式2的频率p2肯定小于模式3的频率p3。模式1的频率p1与p2、p3的大小关系受到l,θ和μ等参数的影响。

图4描绘了3个振动模式。图中黑色V型折线和黑圆点表示中性位置(平衡位置)的分子构型，黑粗箭头表示弹簧变形，而空心箭头表示原子绝对位移，灰色V型折线和灰色圆点表示偏离平衡的振动模式。

图4(a)对应模式一。该模式{φ}1的Δθ=0，因此它只有线弹簧的伸缩(键角不变，角簧无势能)。由于两个线弹簧，AC伸长 (缩短)和BC缩短(伸长)的幅度相等, 所以C沿对称轴的绝对位移为零(如果沿对称轴不等于零，那么就无法保持质心守恒—动量守恒在位移上的表现)。水平方向的质心守恒则要求A和C两个原子的绝对位移水平分量与B的相反。

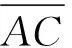
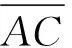
本征振动是围绕平衡位置的周期振动，所以式(10)的各模式乘上-1后，还是对应各自模式。当然图示时，图4中的诸箭头也要变成反向。

2 校验

2.1 二氧化碳

二氧化碳(CO2) 在常温下是一种无色无味、不可燃、不助燃的气体，具有十分广泛的用途；航空燃料燃烧后产物为CO2，后者的红外谱特性对隐形飞行器的监测也有参考意义。

从文[7]有如下参数：l=1.1620Å=1.1620×10-10m,k=16.0mdyn/Å=16.0×10-8N/(10-10m)=1.60 ×103N/m,kA=0.58mdyn·Å/rad=0.58×10-8N×10-10·m=0.58×10-18N·m/rad。μ=mO/mC=16/12(O的相对质量按16计算)。C原子的绝对质量mC=1.993×10-26kg。将上述数据代入式(8)和式(9)可得到

光速按c0=2.998×1010cm/s计算。由上述p1，p2和p3可得到厘米波数

其中υ1和υ3分别与文[7]中2392.2cm-1和1352.8cm-1的实验测量结果很接近(误差分别为4.3%和3.7%)，υ2与文[7]的672.9cm-1差异稍大(误差14.1%)。

对CO2这种直线型对称分子，θ=0，进而式(5)中的c=0。为此式(10)的模式{φ}2应按c→0极限来理解。在这样的理解下，模式2变成{φ}2={0,0,1}T，这正是弯曲模式(bend)。此模式下，键长不变，只有键角的变化, 该模式的势能贮藏于角簧kA。模式3变成{φ}3={2β,2β, 0}T,这是对称伸缩模式。模式1的{φ}1则为反对称伸缩。

2.2 水分子

水是人类生命的源泉。在许多应用中，水含量都是非常重要的指标，可利用水分子振动信息推测水分含量。

水分子(H2O)的参数如下[8]：l=0.9572Å=0.9572×10-10m,θ=104.52°,k=8.454mdyn/Å=8.454×10-8N/(10-10m)=845.4N/m,kA=0.697mdyn·Å/rad=0.697×10-8N×10-10·m=0.697×10-18N·m/rad。μ=1/16=16/12(O的相对质量按16计算;H的按1计算)。C原子的绝对质量mC=1.993×10-26kg。将上述数据代入式(8)和式(9)

由上述p1，p2和p3可得到厘米波数

这分别与文[9]中3756cm-1，1595cm-1和3657cm-1的测量结果很接近(误差分别为6.5%, 6.5%和4.0%)。