单位圆周上具有重极点的Z变换与傅里叶变换相互计算的方法*

陈绍荣，何 健，朱行涛，刘郁林

（1.陆军工程大学通信士官学校，重庆 400035；2.军委装备发展部军事代表局驻成都地区军事代表室，四川 成都 610041；3.重庆市经信委，重庆 400015）

0 引 言

在国内外《数字信号处理》教材及著作[1-4]中，针对序列的DTFT与ZT的互相表出问题，仅给出序列ZT的收敛域包含Z平面的单位圆周和序列的DTFT在Z平面的单位圆周上解析时序列的DTFT与ZT的代换关系。然而，这种简单的代换关系，不是在任何序列情况下均成立。本文将单位圆周上具有重极点的ZT分解成单位圆周上含极点和不含极点两部分之和，将序列的DTFT分解成解析部分与不解析部分之和，研究了序列的DTFT与ZT之间的关系，不仅解决了单位圆周上具有重极点的ZT与DTFT的相互计算问题，而且得到了一些有益的结论。

1 由序列的Z变换确定其傅里叶变换

从逆ZT的计算可知，若双边序列f(k)的Z变换F(z)的收敛域为va＜|z|＜vb，则双边序列f(k)中，因果序列对应F(z)的区内极点zi(i=1,2,…,p)（即|zi|≤va的极点），反因果序列对应F(z)的区外极点ze(e=1,2,…,q)（即|ze|≥vb的极点）。

1.1 若满足条件va＜1＜vb

考虑到va＜1＜vb，则F(z)的收敛域va＜|z|＜vb包含Z平面上的单位圆周z=ejω，那么复变量z可在单位圆周上取值，即可令z=ejω。于是，从序列f(k)的Z变换F(z)获得了序列f(k)的傅里叶变换（DTFT），即：

1.2 若F(z)在Z平面单位圆周上存在极点

由式（2）可知，将F(z)在Z平面单位圆周上的极点分离出来，使F1(z)的收敛域扩大，且包含Z平面的单位圆周z=ejω；F2(z)仅存在区内极点zi(i=1,2,…,p)，且满足max=1。显然，F2(z)的区内极点是F(z)的区内极点，且F2(z)对应的序列F2(k)为因果序列。

（1）若F(z)在Z平面单位圆周上仅存在区内单极点zi=ejωi(i=1,2,…,p)，则式（2）可写成：

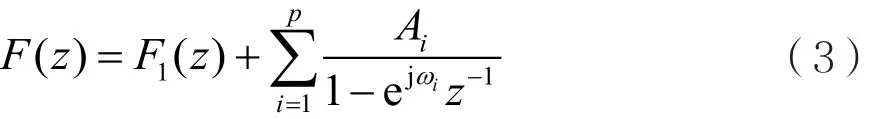
式中，系数Ai(i=1,2,…,p)可利用留数进行计算，即：

式（3）中，将z用ejω代换，则有：

对式（3）取逆ZT，可得：

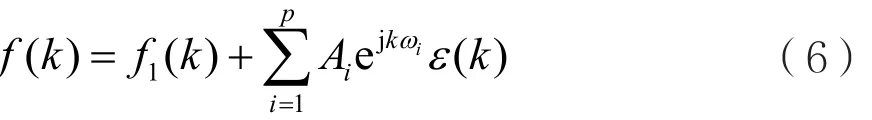
由于：

对式（6）两边取DTFT，并考虑到DTFT的频移性质、式（7）及式（5），则有：

式中，系数Ai(i=1,2,…,p)利用式（4）进行计算。

（2）若F(z)在Z平面单位圆周上仅存在区内n重极点zl=ejωl，则式（2）可写成：

式中，系数Bi(i=1,2,…,n)利用式（10）进行计算，即：

在式（9）中，将z用ejω代换，则有：

对式（9）两边取逆ZT，可得：

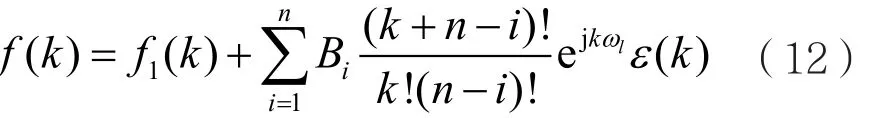
考虑到式（7）、DTFT的频域微分性质及DTFT的时移性质，则有：

同理，可得：

式中， Xλ(ω)=δ ′(ω)−jλδ(ω),λ=1,2。

对式（14）进行推广，可得ZT在Z平面单位圆周上具有 n +1阶极点的因果序列的频谱计算公式，即：

式中， Xλ(ω)=δ ′(ω)−jλδ(ω),λ=1,2,…,n。

对式（12）两边取DTFT，并考虑到DTFT的频移性质、式（15）及式（11），则有：

式中，Xλ(ω)=δ′(ω)−jλδ(ω),λ=1,2,…,n−i，系数(i=1,2,…,n)利用式（10）进行计算。

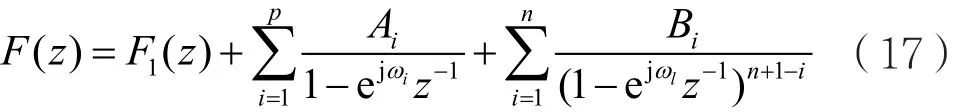
同理，由式（17）可导出式（18），即：

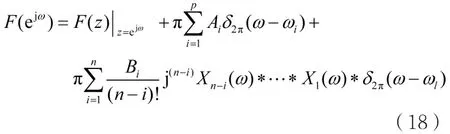
式中，Xλ(ω)=δ′(ω)−jλδ(ω),λ=1,2,…,n−i，系数Ai(i=1,2,…,p)及Bi(i=1,2,…,n)分别利用式（4）及式（10）进行计算。

1.2.2 va＜＜1时

若va＜＜1，则F(z)可写成：

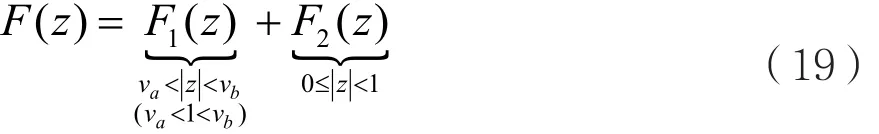
由式（19）可知，将F(z)在Z平面的单位圆周上的极点分离出来，使F1(z)的收敛域扩大，并且包含Z平面的单位圆周；F2(z)仅存在区外极点ze(e=1,2,…,q)，且满足min=1 。显然，F2(z)的区外极点正是F(z)的区外极点，且F2(z)对应的序列F2(k)为反因果序列。

同理，由式（20）可导出式（21），即：

式中，Xλ(ω)=δ′(ω)−jλδ(ω),λ=1,2,…,n−i，系数Ae(e=1,2,…,q)及Bi(i=1,2,…,n)分别用式（22）及式（23）进行计算，即：

1.3 若满足条件va＜＜vb＜1

考虑到va＜＜vb＜1，将F(z)展成部分分式F(z)=F1(z)+F2(z)时，则F2(z)中至少存在一项，其极点z成为F(z)的区外极点，e且满足=vb＜1。若令z=，则Z变换Fe(z)对应的反因果序列(k)=−(−k−1)不满足绝对可和条件，即：

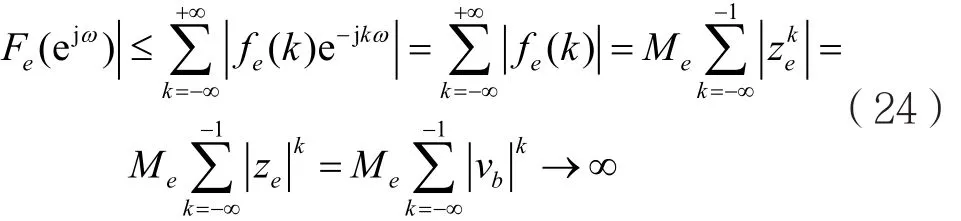
1.4 若满足条件1＜va＜＜vb

考虑到1＜va＜＜vb，将F(z)展成部分分式F(z)=F1(z)+F2(z)时，则F1(z)中至少存在一项其极点z成为F(z)的区内极点，i且满足=va＞1。若令z=ejω，则Z变换Fi(z)对应的因果序列(k)=Mε(k)不满足绝对可和 条件，即：

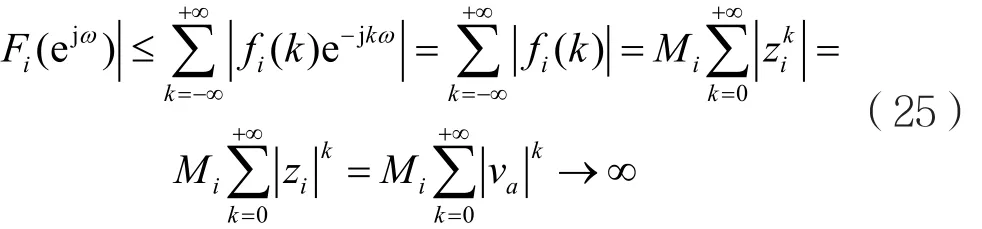
由式（25）可知，Fi(ejω)不存在，因此F(ejω)不存在。

结论1：若序列F(k)的Z变换F(z)的收敛域及收敛域的边界均不包含Z平面的单位圆周z=ejω，则序列F(k)的傅里叶变换F(ejω)不存在。

2 由序列的傅里叶变换确定其Z变换

2.1 若F(ejω)在Z平面单位圆周z=ejω上解析

所谓函数F(ejω)在Z平面单位圆周z=ejω上解析，即表明函数F(ejω)在z=ejω上处处可导，亦即函数F(ejω)的导函数满。因此，函数F(ejω)在Z平面单位圆周z=ejω上解析，意味着Z平面单位圆周z=ejω应包括在F(z)的收敛域va＜＜vb内，即va及vb应满足va＜1＜vb。当然，可以直接将ejω换成z，即：

当获得F(z)后，其收敛域可用一个与单位圆周重合但能内外移动的圆周搜索决定：往内碰到F(z)的第一个极点，就是收敛域的内边界圆周=va；往外碰到F(z)的第一个极点，就是收敛域的外边界圆周=vb。

2.2 若F(ejω)在Z平面单位圆周z=ejω上不解析

因为函数F(ejω)在Z平面单位圆周z=ejω上不解析，所以单位圆周z=ejω应在F(z)的收敛域之外，不能直接将ejω换成z。双边Z变换F(z)有可能不存在，也可能存在。即使存在，单位圆周z=ejω将会是F(z)收敛域的边界，F(z)收敛域的可能形式是1＜＜vb或va＜＜1。否则，连F(ejω)都不存在。

首先通过部分分式展开，将F(ejω)分成在Z平面单位圆周z=ejω上解析的F3(ejω)及在Z平面单位圆周z=ejω上不解析的F4(ejω)两部分，再进行分析和研究。

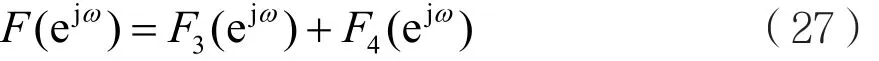
（1）若Z平面单位圆周z=ejω上不解析的部分(ejω)是由冲激函数及其导数构成。

①若Z平面单位圆周z=ejω上不解析的部分(ejω)具有式（17）的形式，则有：

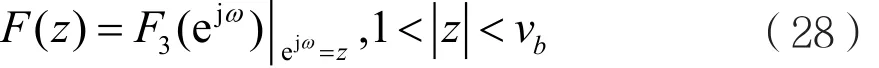
②若Z平面单位圆周z=ejω上不解析的部分(ejω)具有式（21）的形式，则有：

（2）若F(ejω)仅存在Z平面的单位圆周z=ejω上不解析部分F(ejω)=F4(ejω)，则F(z)不存在。

结论2：由于常数序列、无时限序列、周期序列、符号函数序列、[Sa(k)]n序列（其中，n为正整数）的傅里叶变换F(ejω)，仅存在Z平面单位圆周z=ejω上不析部分，即F(ejω)=F4(ejω)，因此，这些序列的双边Z变换F(z)不存在。

3 应用举例

例3.1：若已知象函数：

试求傅里叶变换F(ejω)。

利用式（4）计算系数Ai(i=1)，可得：

利用式（10）计算系数Bi(i=1,2,3)，可得：

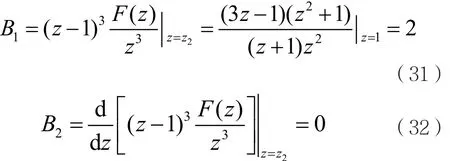
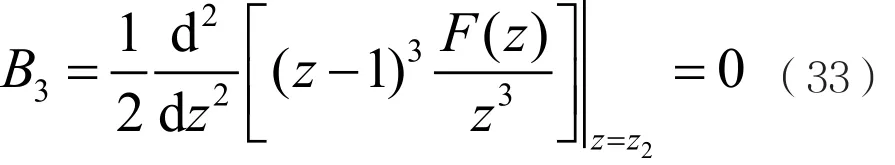
由式（18）可得：

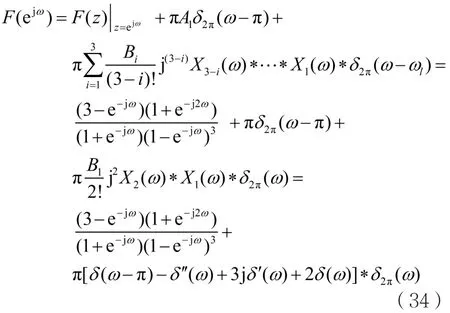
例3.2：若已知象函数：

试求傅里叶变换F(ejω)。

解：考虑到：

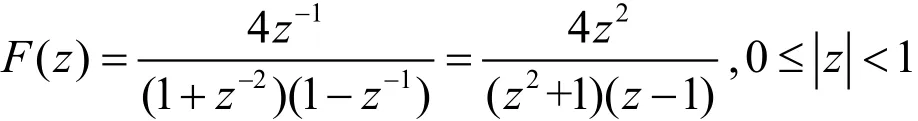
令(z2+1)(z−1)=0 ，得3个区外单极点

利用式（22）计算Ae(e=1,2,3)，可得：

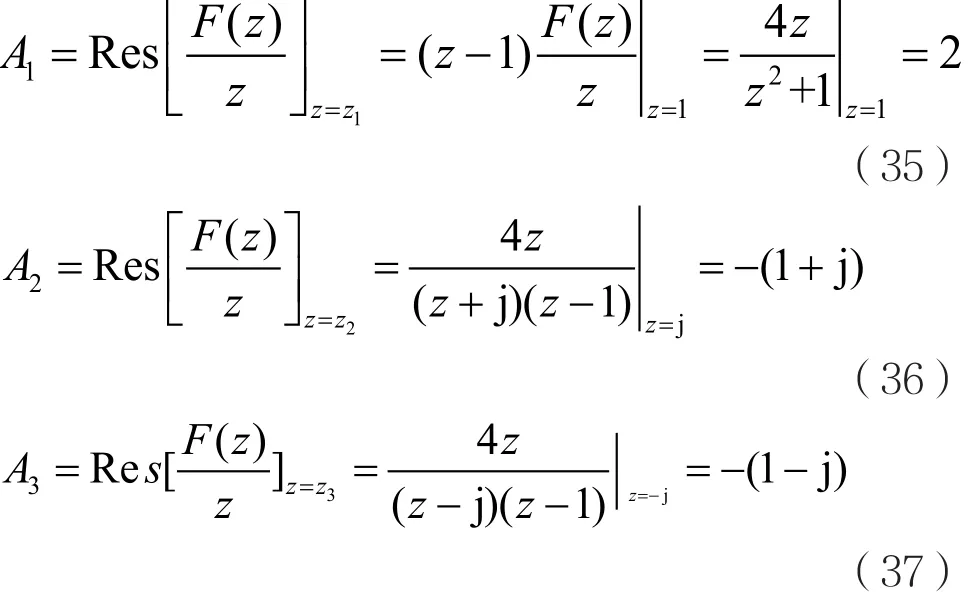
由式（21），可得：

4 结 语

本文基于分解的基本思路，将单位圆周上具有重极点的ZT分解成单位圆周上含极点和不含极点两部分之和。针对单位圆周上含极点的ZT部分，分区内极点和区外极点两种情况进行了深入研究，揭示了单位圆周上仅存在区内重极点的因果序列的频谱计算公式；将序列的DTFT分解成解析部分与不解析部分之和，对其不解析部分进行了详细讨论。这不仅解决了单位圆周上具有重极点的ZT与DTFT的相互计算问题，而且得到了一些有益的结论。