打破思维定势 激发创新思维

朱红芳

苏州市吴江区北厍中学 江苏苏州 215200

古语云“文无定法，思无定式”，数学传统的教学方法过多地强调了老师讲的程式，学生按部就班解题，这对于初学者来说不失为一种入门法，但无形中也给学生划定了一个框架，束缚了学生的思路，学生碰到“变式题”，只能望题兴叹，陷入思维定式的陷阱。要改变这种状况，老师必须强化辅导环节，根据学生实际思维水平设计教学内容，重点放在如何开拓思路上，多给学生留下思维的空间，培养良好的思维品质，营造思维的绿洲。

一、培养思维的探索性

苏霍姆林斯基说过：“在人们的心灵深处，都有一种根深蒂固的需要，这就是希望感到自己是一种发现者、研究者。”数学基础比较好的学生，老师可以根据教学内容巧设疑难，加以适当的启发后让学生观察、思考、分析、对比，养成探索的习惯，提高探索的兴趣。

我在教因式分解的拆项、添项法时，先布置这样一道题“分解因式：1、x2-y2-z2-2yz；2、x3-2+2x2-x；3、x3-2x2+3”其中第“3”题学生无法可想，我引导学生在公式法中想办法，（a +b）2展开式为什么是三项，（a+b）(a-b)的积为什么是二项，让学生领会并项与逆向的拆项。于是就有学生提出将其中的一项拆为两项，再找分组的可能性，将“-2x2”项拆为-3x2+x2或者-4x2+2x2等等，启发他们对拆法提出要求。并问：有规律吗？“x3”这项能拆吗？“+3”这项能拆吗？让他们找出拆法；接着我指出缺项系数是0，把这项0拆就成了添项，让学生思考：这里能否用添项的办法？添上3x-3x是否使它具有分组条件？添上4x-4x行否？添项时要注意什么？最后，学生能根据多项式x4+4的特征，采用添项法分解因式。

二、培养思维的灵活性

义务教育数学大纲指出，初中数学中辩证唯物主义教育的一个因素是“数学内容中普遍存在的运动变化、相互联系、相互转化等观点”，要求培养学生的观察能力，类比分析、综合串联的能力。作为教师，也应培养学生用运动变化、寻找联系、相互转化的观点来思考问题，这就是培养思维的灵活性，做法是观察、联想、转化，从内在联系得到求解的方法。

例如，苏科版教材七年级下册“期末复习全等三角形”时，我设计了如下的例题：如图1，已知点C是线段BE上的一点，△ABC，

△CDE都是等边三角形，求证

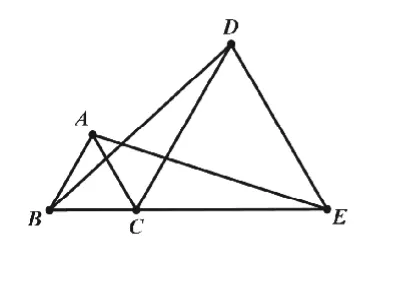
图1

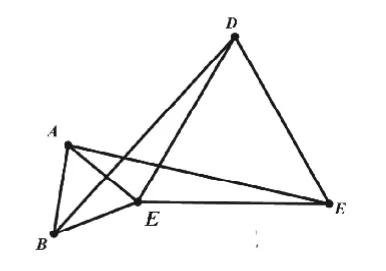
图2

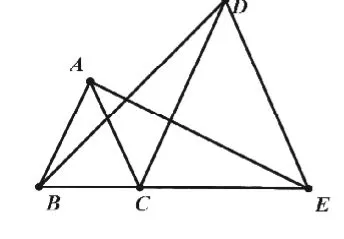
图3

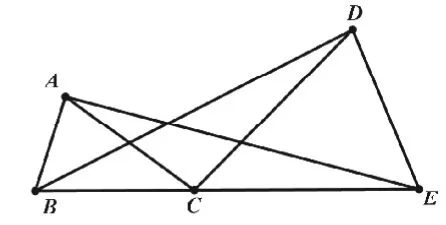
图4

【变式1】如图2，将△CDE绕点C按顺时针方向旋转角后，以上结论是否成立？为什么？

【变式2】将等边三角形改为等腰三角形，结论成立吗？学生展开了以下讨论：

（1）结论不成立。以BC、CE为底的等腰三角形（如图3）

（2）结论成立。以BC、CE为底的等腰三角形（如图4）

这样设计问题具有变通性，它有助于学生抓住问题的本质，从中寻找他们之间的内在联系，探索出一般规律，从而提高学生的思维品质。它有助于激发学生探索问题的兴奋点，让学生在解开放性问题的过程中对问题从不同角度进行探索，从不同层面进行分析，克服思维定势，避免思维僵化，从而有助于全面深刻地认识问题，灵活多样地处理问题，它能较好地培养学生思维的灵活性。

三、培养思维的周密性

思维具有周密性，才能全面地看问题，才能既综观全局，又不忽略重要的细节。初中学生开始从幼稚向成熟过渡，他们的思维情感在发生变化，经验阅历又不足，对所学知识的全面理解也不够，于是在研究较复杂的问题时，常难于深入全面地分析问题，不能透过现象抓本质。为改变这种情况，应先让学生探索问题，然后把学生的思维活动展开，针对学生分析上存在的缺陷进行引导，让学生去抓住事物本质规律去作出周密的思考。

在具体教学中，连续地构造知识系统，使新获得的知识和技能纳入学生原有的知识系统，以保持思维的周密性。学“圆”这部分知识时，学生感到知识点多、很零乱，教师给予适当点拨。圆是三角形、四边形与它的知识的有机结合，是初中几何达到了最精彩的部分，例如三角形与圆的结合：圆内接三角形的外心就是外接圆的圆心；圆外切三角形的内心就是内切圆的圆心；圆内接正三角形的边长与外接圆的半径之比为根号3比1。又如四边形与圆的结合：圆内接四边形的对角互补，圆内接梯形一定是等腰梯形，圆内接平行四边形一定是矩形；圆的外切四边形的两组对边的和相等。通过这样的点拨，使前后知识融为一体，使知识系统化，温故而知新，培养了学生思维的周密性。

四、培养思维的创造性

当前初中数学教学进行素质教育的一个重要方面就是培养学生的创造思维能力。初中学生研究问题习惯于按照常规思考，受定向思维约束，对有些关系隐含、曲折的问题常会感到无计可施。教师在带领学生对问题进行探索时，应引导学生摆脱原有知识范围的羁绊和定向思维的制约，利用题中隐含的条件，把头脑中已有的知识信息重新组合，发现新问题，标新立异，另辟捷径。

在例题教学上，要适当运用变式，讲究逐步设置障碍，不断增加创造性因素，达到举一反三的目的。例如，如图5，△ABC各边长都大于2，分别以A、B、C为圆心，以1为半径画圆，求阴影部分的面积。

分析：我们可以让学生把三个阴影部分剪下来，重新拼图，从而就可以得到一个半径为1的半圆，故阴影部分的面积为

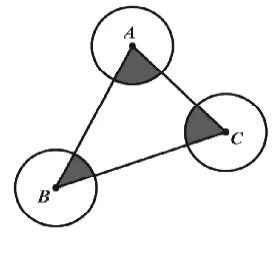
图5

图6

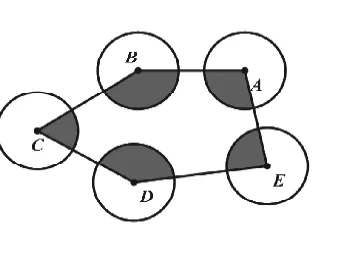
图7

对于这道题，如果我们就此结束的话，并不能引起学生的共鸣。我们可以对这个问题进一步探索：

【变式一】如图6，把题目中的△ABC换成四边形ABCD，其他条件不变，求阴影部分的面积。

分析：重新拼图，从而就可以分别得到一个半径为1的圆，故阴影部分的面积为。

【变式二】如图7，把题目中的△ABC换成五边形ABCDE，其他条件不变，求阴影部分的面积。

分析：重新拼图，从而就可以分别得到一个半径为1的圆和一个半圆，故阴影部分的面积为。

【变式三】把题目中的△ABC换成n边形，其他条件不变，求阴影部分的面积为。

分析：经过前面两个变式题的理解，我们可以掌握一般性的规律，将阴影部分剪下来，重新拼图可以得到几个圆，用的圆，然后再乘以 ，则阴影部分

【评注】本题是从具体的情况入手，如此下去，猜想第n次的结果，这样让学生感受从特殊到一般的转换，或感受从平面到空间的转换，让学生去感知知识的再现过程，这样有利于培养学生的综合解决问题的能力，充分挖掘学生的潜力，培养学生猜想、归纳能力，更有利于培养学生综合能力，使学生的综合素质有较大的提高。这样的变式，遵循了循序渐进的原则，使学生一步一个台阶，体会到成功的喜悦，极大地激发了学生的积极性、创造性。

综上所述，要打破学生一贯的思维定式，开创异彩纷呈的数学教学新局面，必须鼓励学生求新、求异、求变，树立他们的创新意识，学会一题多思，一题多解，多角度的思维方式，拓宽学生思路，营造思维的绿洲。