冷却塔风振效应特征及影响因素分析
2018-09-28张军锋杨军辉葛耀君
张军锋, 杨军辉, 葛耀君, 赵 林
(1. 郑州大学 土木工程学院,郑州 450001;2. 同济大学 土木工程防灾国家重点实验室,上海 200092)
风荷载是冷却塔的设计控制荷载,其动力作用作为冷却塔结构的关键问题之一,长期以来一直受到设计和研究人员的关注[1-2]。作为高耸空间薄壁结构,冷却塔风振效应的影响因素众多,包括紊流度、风速取值V、结构尺度L、结构基频fmin以及阻尼比ζ等,但大多研究都是在特定参数下分析冷却塔的风振效应[3-10],并未系统分析上述参数的影响。近年来,随着我国冷却塔建设高度的持续增加且壁厚相对更薄,结构愈加轻柔,冷却塔对风荷载的动力作用将更加敏感,亟需明确其风致动力响应特征及影响因素。
实际上,已有学者对上述因素的影响展开研究,但分析方法、参数取值及具体结果等都仍有较大差异。文献[11]仅分析了阻尼比ζ对共振分量的影响,但其计算风速高达100 m/s,现实中并不会出现。文献[12]通过对三座冷却塔的计算分析了结构基频fmin对风振效应的影响,但其所得结果实际上还同时受结构尺度L的影响。另外,文献[12]均选择位移作为参考指标,但冷却塔结构设计的控制指标是内力而非位移,且内力和位移的风振效应是不同的。文献[13-14]虽考虑了多个因素,但每种因素仅考虑2~3个参数值,无法得到系统的变化规律。文献[15-17]分别经试验和计算分析,给出了综合考虑V,L和fmin等多因素的表达式,并分别被英国和德国规范采纳,但具体结果和应用形式亦不相同[18]。而我国规范[19]仅区分场地类型也即紊流度给出了风振系数取值,对其他因素并未涉及。这都说明对冷却塔风振效应的影响因素还未有系统和明确的认识。
由于新建冷却塔几乎都位于城镇郊区,也即我国规范中的B类地貌,其紊流度基本是确定的;结构尺度L则通过影响结构动力特性和风荷载表面相关性而最终影响风振效应,这三种因素实际难以独立分析。因此本文以待建某内陆核电厂大型冷却塔为例,通过刚体模型风洞试验和结构动力响应时程计算,在前期风致动力响应特征的基础上,通过调整阻尼比ζ、风速取值V和风压子午向相关性,分析这三个因素对风振效应的影响。
1 工程背景与计算方法
本研究中的冷却塔(见图1)处B类场地,10 m高度基本风速V0=26.7 m/s,对应塔顶风速VH=40 m/s。对塔筒表面位置的描述区分环向和子午向两个维度,环向角度θ以迎风点为0°,逆时针转动为正;子午向以0≤hS/HS≤1表示塔筒相对高度位置。
试验在同济大学TJ-3风洞中进行,模拟B类地貌,几何缩尺比λL=1∶ 200,采用适当措施进行雷诺数效应补偿。塔顶试验风速10 m/s,即风速比λV=1∶ 4,并由此可得时间比λt=1∶ 50。信号采样频率312.5 Hz,采样时长19.2 s,每个测点6 000个数据。限于设备采集能力,仅测面A的9排断面同步测量并用于时程计算,图2给出了侧面A断面的平均风压、脉动风压以及依Davenport理论所得峰值因子g,图2中各断面的参考风压均为本断面高度的来流速压。试验及结果的详细介绍可见文献[20]。
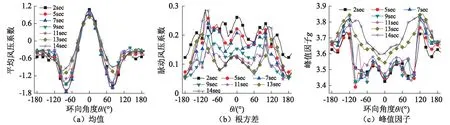
图2 不同断面的环向风压参数 Fig.2 Wind pressure parameters of different sections
采用ANSYS程序进行结构计算,塔筒采用Shell188单元模拟并划分72×35(环向×子午向)个单元,下支柱和檐口采用Beam188单元模拟。结构前100阶频率分布在0.763~2.903 Hz,且各阶频率基本随阶数线性增加。此频段范围内的振型可分为三种[21](见图3),即双向谐波耦合振型、侧弯振型和竖向伸缩振型,并以第一种为主导:三种振型分别有95个、4个和1个。动力计算采用直接积分法进行,风荷载时程采用风洞试验结果,根据风速比λV和时间比λT换算到原型结构,并通过POD(Proper Orthogonal Decomposition)分解和预测,将9×36=324个风压测点扩展到36×72=2 592个有限元节点;时间积分步长Δt=1/37.5 s,涵盖前53阶模态(f53=1.842 Hz),且即使将Δt降低一半,脉动响应的增幅亦不足2%;采用瑞利阻尼,各阶模态阻尼比ζ约为1%;对于结构响应,直接以时程最值作为极值。除采用上述直接积分法进行计算外,还采用模态叠加法进行了校核计算,除FX外,两者所得脉动响应误差一般不超过1%。
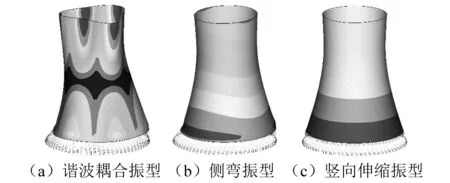
图3 结构典型模态Fig.3 Characteristic modes of the HCT
众所周知,风对结构的动力效应体现在两个方面,即自然风本身的脉动性以及其引发的结构惯性效应(包含阻尼效应)。结构风振效应在最初较长的时间里以频域计算为主,并且脉动响应σ也相应地被近似划分为背景分量σB和共振分量σR[22]:式(1)~式(3)以单自由度结构的位移响应为例给出了其计算表达式。其中k,f0为系统的刚度和频率,S(f)为荷载P(t)的频谱。
(1)
(2)
(3)
类似地,背景和共振响应在时域内也可进行划分。式(4)以单自由度为例给出了时域内的动力学方程,其中m,c分别为系统的质量和阻尼,且c=2m2πf0ζ。如果忽略系统的惯性效应,则式(4)退化为式(5)。显然,式(5)中的响应yB(t)完全是由自然风本身的脉动性引起的,也是精确意义的背景响应,并可直接通过拟静力计算求得。此时将y(t)与yB(t)相减(见式(6)),则可得共振分量yR(t)。显然,σ,σB和σR分别与y(t),yB(t)和yR(t)对应,下文对背景和共振分量的划分也以时域方法为准。
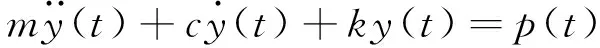
(4)
kyB(t)=p(t)
(5)
yR(t)=y(t)-yB(t)
(6)
2 计算结果及分析
2.1 计算结果概述
图4首先给出了基准工况下(ζ=1%且λT=1∶ 50)部分塔筒内力及位移的均值和阵风响应因子G沿塔筒高度的分布,包括子午向轴拉力FY,T,环向轴拉力FX,T,环向内凹和外凸弯矩MX,I、MX,O,内凹和外凸位移UI,UO,且均以幅值给出。可以看出,不同响应的均值响应和动力效应差别极为显著,对其详细分析参见张军锋等的研究。总的来说,除塔筒顶部0.2HS高度范围,双向轴力和位移的风振效应均较小而MX的风振效应显著,在塔筒顶部,各内力均值响应下降而脉动响应提高,故风振效应均甚为显著。需要注意的是,众多文献对冷却塔的动力计算仅关注其FY,T,忽略了其环向受力,但计算表明,环向弯矩MX的G值明显大于FY,T,所阅文献中,只有文献[23]在未考虑共振效应的计算中关注了MX且与张军锋等的研究有相同的结论。冷却塔风荷载作用下的结构设计控制指标则有塔筒中下部的FY,T、塔筒上端局部区域的FX,T以及环向弯矩MX,下文则通过调整计算参数分析对上述响应的影响。
为进一步分析脉动响应特征,表1给出了ζ=1%时4个特征位置(A点为hS/HS=0.19,θ=0°;B点为hS/HS=0.49,θ=0°;C点为hS/HS=0.70,θ=-95°;D点为hS/HS=0.92,θ=-95°)内力的平均和脉动响应。其中:A点和B点位于塔筒中下部的迎风子午线,主要关注其FY,T;C点和D点位于塔筒中上部的侧风区,主要关注其环向轴拉力FX,T;同时还关注4个位置的环向弯矩MX。
从表1可知,ζ=1%时,双向轴拉力的总脉动响应σ都远小于其均值E,σ/E仅为1/5.8~1/7.6,且FX,T的σ/E,或者说FX,T的脉动效应,略大于FY,T的σ/E;MX的E和σ则在同一量级,甚至在C、D两点各个阻尼比下都有E<σ,这也说明MX的脉动效应较双向轴力更为显著,这也是图4中弯矩的G极为显著而双向轴拉力的G相对偏小的原因。在脉动响应中,双向轴拉力的σR也都明显小于其σB,背景分量在总脉动响应中的比例σB/σ为85%~95%,且亦有FX,T的σB/σ略小于FY,T的σB/σ,说明FX,T的共振分量权重较FY,T略大;而MX的σR则和σB接近,甚至有σR>σB,说明共振分量在MX的脉动效应中占有较大的权重。也正因为MX的共振分量权重较大,本文MX的G值为3~6,而Abu-Sitta等的研究在忽略共振分量时所得MX的G值为2~3。
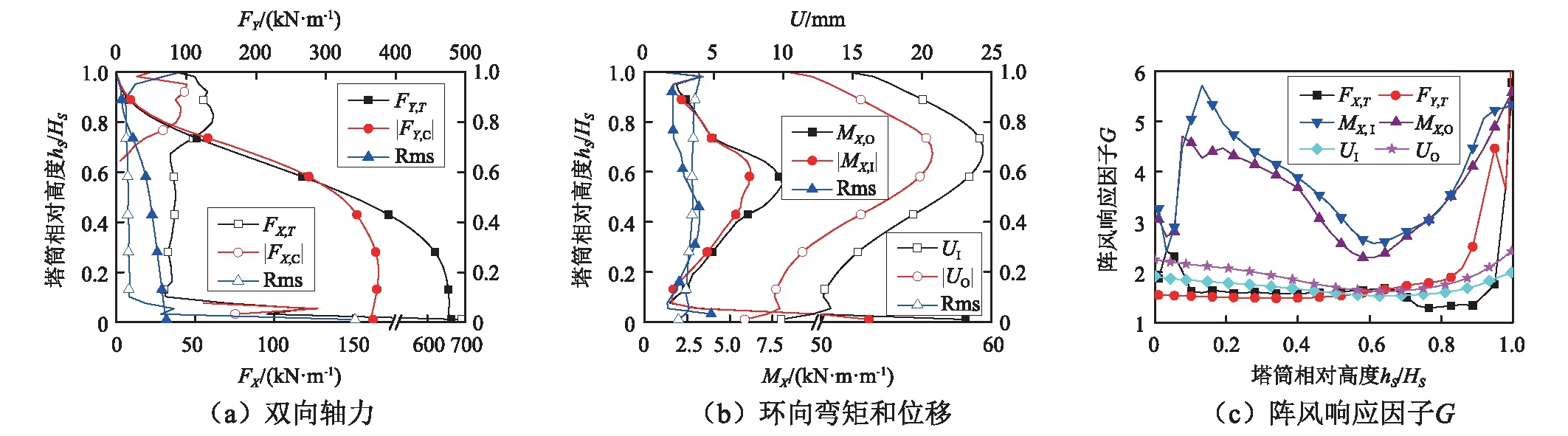
图4 各响应的均值和阵风响应因子GFig.4 Mean responses and gust response factors
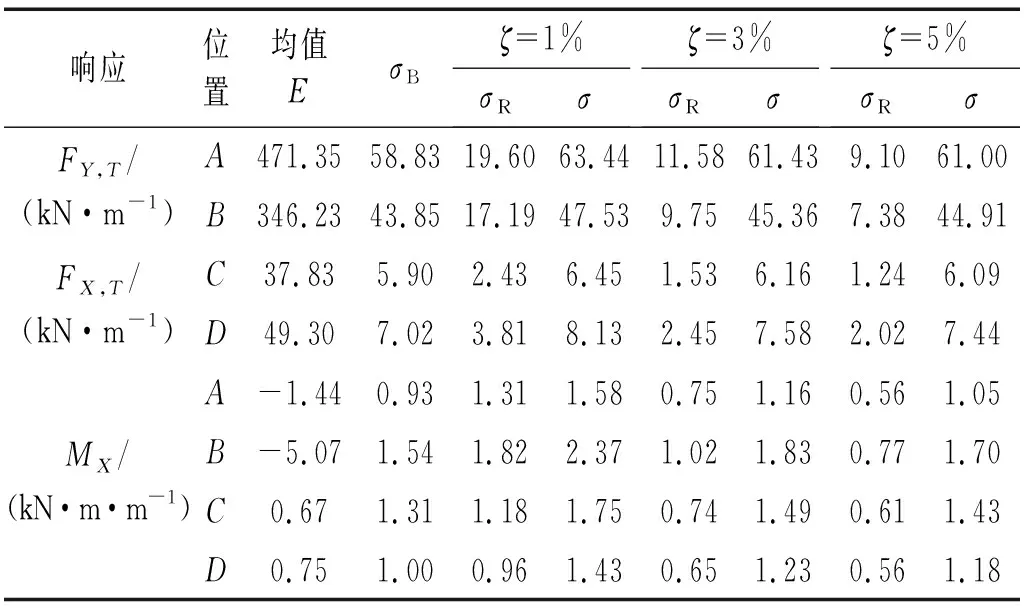
响应位置均值EσBζ=1%σRσζ=3%σRσζ=5%σRσFY,T/(kN·m-1)A471.3558.8319.6063.4411.5861.439.1061.00B346.2343.8517.1947.539.7545.367.3844.91FX,T/(kN·m-1)C37.835.902.436.451.536.161.246.09D49.307.023.818.132.457.582.027.44MX/(kN·m·m-1)A-1.440.931.311.580.751.160.561.05B-5.071.541.822.371.021.830.771.70C0.671.311.181.750.741.490.611.43D0.751.000.961.430.651.230.561.18
上述3个内力脉动效应(σ/E)的大小以及共振分量在总脉动分量中权重(σR/σ)的大小关系,实际上也是冷却塔结构受力特性的表现[24-25]:MX属于局部内力,主要受其附近位置风压的影响,而FY则属整体内力,与整个塔筒表面的风压有关,显然,大面积风压的叠加组合使其脉动性下降。
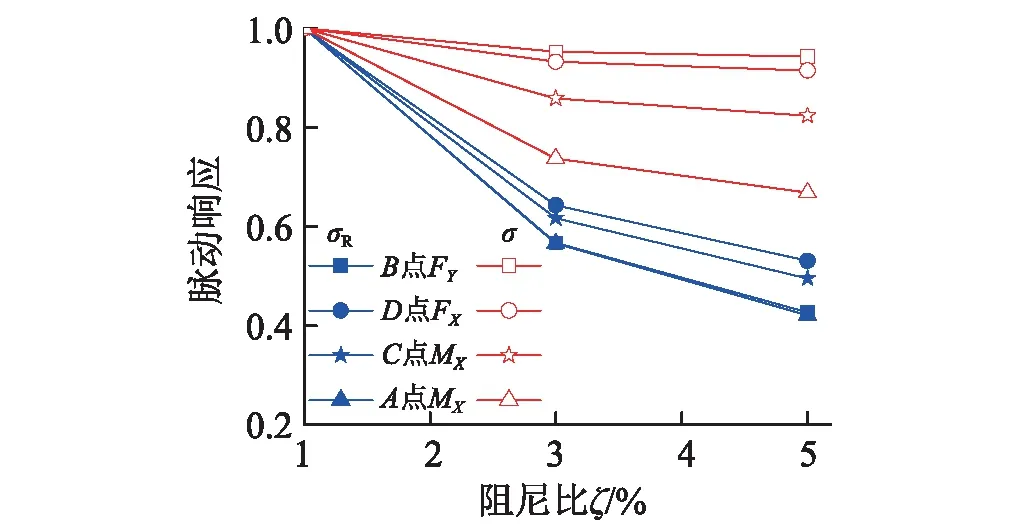
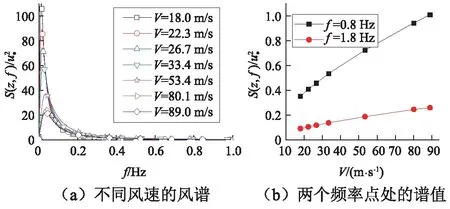
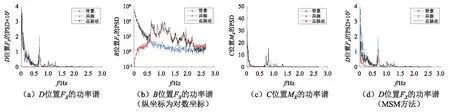
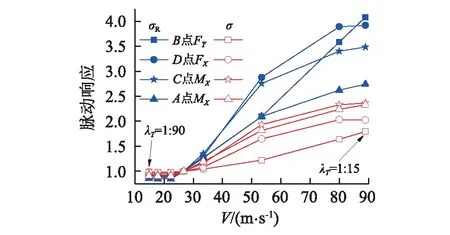
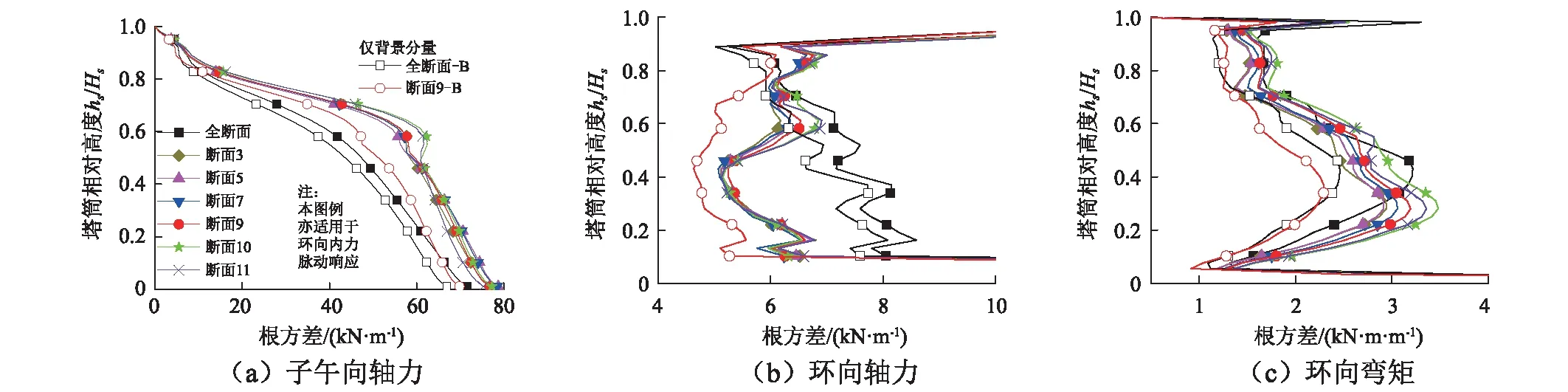
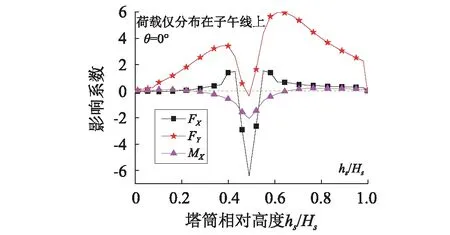
另外,从图9可知,如忽略共振分量,对于FY,hS/HS<0.5,0.5 图5 脉动响应随ζ的相对变化Fig.5 Gust responses for different damping ratios 另外,鉴于前文对背景和共振分量的划分,两者之间将存在一定的耦合分量。如果依然根据σB和σR以式(1)近似计算总脉动响应σ,表1中各内力σ的误差均小于5%,说明实际的耦合分量极小。这也是因为冷却塔表面的风荷载频谱能量主要集中在0.5 Hz以下(见图6),而结构基频为0.763 Hz,所以背景和共振分量之间几乎没有耦合性(见图7):在低于0.5 Hz的频段,总脉动响应的功率普曲线与背景响应重合;而在高于0.7 Hz的频段,总脉动响应的功率谱曲线则与共振响应重合,而在0.5~0.7 Hz的背景和共振分量虽有一定的耦合效应但幅值极小。同时,各分量的频谱分布也是对表1脉动响应数值的一个验证。另外,对比各内力共振分量的功率谱分布可知,同一振型对不同内力共振响应的贡献并不一致:图7中3个内力共振分量的贡献分别主要来自0.7~0.8 Hz,0.7~0.9 Hz且1.2~1.4 Hz以及0.8~1.0 Hz之间的振型。并且从图7还可知,各响应共振响应都主要分布在0.7~1.6 Hz,与本计算的截取频段(<1.84 Hz)一致,也说明积分步长Δt取值合理。 图6 脉动风风速频谱Fig.6 Davenport wind velocity spectrum 图7 特征位置内力响应的功率谱密度Fig.7 PSD of three internal forces 需要说明,由于FY的共振分量相对极小,所以在图7(b)以对数坐标给出以便于辨识。图7(d)还给出了模态叠加法所得的FX频谱,与完全积分法所得结果(见图7(a))对比可知,前者总脉动响应的频谱在低频段偏小,但其共振分量在0~0.5 Hz仍有分布,而这显然是不合理的。这一现象也使模态叠加法所得σ小于完全积分法的结果,而σR大于完全积分法的结果。模态叠加法出现这种结果的具体原因有待进一步分析,所以本文所给均为完全积分法的结果。 尽管本冷却塔设计风速下因风谱能量集中的区段低于结构基频,共振效应较弱,但如果设计风速增加,脉动风的频谱渐趋高频(见图6),结构共振效应σR在总脉动响应σ中的权重也将增加:因为σR不仅与荷载幅值有关,还与荷载频谱分布和结构动力特性有关。为得到不同风速下的响应,可在保持λL=1∶ 200不变的情况下对λV=1∶ 2.22~1∶ 13.33和λT=1∶ 90~1∶ 15进行调整,以分析风速变化对共振和总脉动响应σR和σ的影响。但这样实际上同时调整了荷载幅值和频谱分布,不便于独立分析荷载频谱分布的影响。 众所周知,对于线弹性结构的动力响应,如果荷载p(t)的时频特征不变而仅是幅值变化,则各响应的时频特征亦保持不变,响应的各个特征值如E,σB,σR和σ均正比于荷载幅值,各响应的峰值因子g和最终的阵风响应因子G亦保持不变。所以,对λV=1∶ 13.33 &λT=1∶ 15的计算,可将其时程结果乘以系数(15/50)2,以屏蔽荷载幅值的影响而仅计入频谱变化的影响。这也相当于在保持λV=1∶ 4不变的情况下仅调整λT=1∶ 90~1∶ 15来分析荷载频谱变化对共振和总脉动响应σR和σ的影响,即将原型结构风压时程在保持幅值不变的情况下,将时间坐标轴从960 s(λT=1∶ 50)逐渐拉伸至1 728 s(λT=1∶ 90)或压缩至288 s(λT=1∶ 15),以分别得到相当于V0=14.8 m/s和V0=89 m/s的频谱:显然,此过程中的平均和背景响应保持不变。另外,我国规范的V0取值绝大多数在33.4 m/s(即λV=1∶ 5 &λT=1∶ 40)以下,过高V0下的结构响应计算并无实际意义,因此可仅关注响应随荷载频谱的变化而忽略荷载幅值的影响。 图8给出了4个位置内力共振和总脉动响应σR和σ随风压频谱的变化,其横坐标仅表示此风速下的频谱而不计其幅值。由图8可知,脉动响应仅在V>22.3 m/s的区段有所变化,说明在V<22.3 m/s时,风压频谱在0.763 Hz以上区段不再随风速变化,故脉动响应趋于稳定。在V>22.3 m/s时,随着V的增加,因荷载频谱趋向高频,各内力的σR都显著增加,但增幅并不完全一致,这也说明同一振型对不同内力共振响应的贡献并不一致。由于σR对σ的贡献有限,所以λT增加时,σ的增加相对较小,并且依然以双向弯矩的增加最为显著,FX其次,FY最小。 另外,即使是现阶段高200 m的冷却塔,其基频也一般在0.7 Hz以上,而设计基本风速V0多在30 m/s以下,由此及风速频谱分布可知,冷却塔的共振分量在总脉动响应中的比重依然很小。 需要指出,在V>22.3 m/s时,随着风速V增加所带来的风压频谱的变化,各内力的σR基本随风速V呈线性增加。这也是因为,在0.763 Hz以上的区段,每个频率的能量也基本随风速线性增加(见图6)。如果再考虑风速增加所带来的风压幅值的增加,则各内力的σR将与V3成正比:本次计算中,塔筒4个高度位置(hS/HS=0.19,0.35,0.49,0.70)迎风点的FY的σR与V2.85~3.25成正比,与预期相符。然而,文献[15-17]分别经计算、试验和计算指出,对于塔筒中下部的FY,其σR分别与V3.4~3.75,V4,和V3.35成正比。其中,Armitt等的研究因模型基频偏小且计入了群塔干扰效应,故其所得σR最为显著,风速V的幂指数也最大;Hashish等和Niemann的研究只是简单给出了σR与V的关系,并没有详细的计算结果。相比之下,本文所得幂指数虽略有偏小,但可从风谱能量随风速的变化规律(见图6)给予解释。 部分学者根据实测或试验风压进行风振响应计算时,由于测点仅布置在一个断面,所以不得不假定脉动风压在子午向完全相关[27-28],或者采用假定的子午向相关系数进行计算,且完全相关与部分相关所得风振 响应亦有差异。又因风压环向相关性的研究较多且结论较为一致,本节在保持环向相关性的基础上,仅在子午向考虑完全相关和部分相关两种情况进行分析。 图8 脉动响应随时间比λT的变化Fig.8 Gust responses for different λT 前述计算采用了整个塔筒表面的风压,已计入了风压在子午向实际的部分相关性。为实现子午向的完全相关,对试验数据进行如下调整:选择某一断面z0的脉动风压时程为基准,其环向θ位置测点的脉动风压时程为cP(z0,θ,t),则任意位置(z,θ)的脉动风压时程为 (7) 式中:σP(z,θ)和σP(z0,θ)分别为所求位置及参考位置的脉动风压根方差。如此,既可保留各断面测点风压的根方差幅值,又可使不同断面之间同一θ位置的测点风压时程完全相关。由于塔筒表面各测点的平均风压并未改变,结构的均值响应E亦保持不变。分别取多个断面的风压作为基准进行调整及计算,图9给出了几种风压所得内力的根方差。另外,为了说明子午向相关性对脉动响应σ的影响,还给出了原始全断面风压和以断面9为基准所得全相关风压的背景分量σB。 图9 子午向相关性对脉动响应的影响Fig.9 Influences of meridian correlation on gust responses 由于保留了各断面脉动风压的根方差幅值,所以选取不同基准断面所得内力根方差基本一致,尤其是对双向轴力;只是不同基准断面内的风压频谱及断面内的相关性存在一定差异,所以各自所得内力脉动响应仅略有差异,下文分析仅针对以断面9为基准所得全相关的结果。 与全断面风压结果相比,子午向全相关的风压使FY的脉动响应σ在各高度位置都有较为明显的增加,尤其在塔筒中部区段:塔筒中下区段(hS/HS<0.7)σ的增幅在10%~50%,且增幅沿高度的增加而增加;上部区段σ的增幅又沿高度急剧回落至零。这是因为FY的脉动响应以背景分量σB为主,并且从内力影响线(见图10)可知,FY受整个塔筒高度范围内荷载的影响,所以当采用子午向全相关风压时,其背景响应σB有明显增加,从而使总脉动响应σ亦明显增加。 图10 B点位置的内力影响线Fig.10 Influence lines of internal forces at position B 脉动响应σ的增加也使FY的G值有显著增加,尤其是在中部区段:在hS/HS=0.3和0.7两个位置,G值分别从部分相关的1.48和1.73提高到约1.57和2.12。考虑到自重在子午向产生的压力,风荷载子午向拉力的些许增加就将使荷载效应组合中的净拉力显著增加,因此,假定子午向风压完全相关时,FY的脉动响应和最终配筋都将会有显著增加。 对于环向内力,采用子午向全相关风压时,塔筒不同高度位置FX和MX的脉动响应σ各有增减,且增减幅值并不显著,塔筒中下区段FX的σ甚至下降约25%。这是由于FX的脉动响应仍以σB为主,但其主要受相邻高度区域内荷载的影响,而此区域内的影响线存在反号,所以FX的σB和σ随子午向相关性的增加而减小。MX依然主要受相邻高度区域内荷载的影响且影响线符号恒定,而区域外的影响线幅值虽小但符号相反,所以MX的σB随子午向相关性的增加无明显变化,仅在中部区域下降约10%。另外,对于MX的σ,其受子午向相关性的影响亦不明显。 需要说明,限于篇幅,上述内力σB与子午向相关性的关系仅是借助θ=0°子午线上的荷载与B点位置内力影响线的定性分析,实际上应根据影响面进行分析。对于结构设计来说,尽管MX的σ在塔筒下部区段有明显增加且使此区域MX的阵风响应因子G也增加约10%,但考虑到FX的σ有所下降,且风荷载的环向内力在多荷载效应组合中的权重有限,其对结构配筋设计的影响也可以忽略。 以风洞试验所得风压为基础,通过风振计算分析了塔筒各响应的风振特征,并探讨了阻尼比ζ、风速取值V和风压子午向相关性这3个参数对风振效应的影响,主结论要如下: (1)除塔筒顶部0.2HS高度范围,双向轴力和位移的风振效应均较小而MX的风振效应显著,在塔筒顶部,各内力的均值响应下降而脉动响应提高,故风振效应均甚为显著。在总脉动响应σ中,各内力背景分类σB和共振分量σR的耦合性均极小,可以忽略。其中,双向轴力的σR均明显小于其σB,σB/σ为85% ~95%,即脉动响应以背景分量为主,而MX的σR则和σB接近,甚至有σR>σB,即共振分量贡献显著。 (2)各内力共振分量σR对总脉动响应σ的贡献随高度位置变化。忽略σR时,在塔筒中下区段,双向轴力的σ下降不超过10%,而MX的σ下降约20%;在塔筒上部,各内力的σ均下降约20%~30%。对于结构配筋设计来说,FY的σR可以忽略而塔筒中上区段环向内力的σR不可忽略。 (3)随阻尼比ζ的增加,各响应的共振分量σR基本按统一规律显著下降,且近似符合式(3)的量化关系。但由于各内力σR对σ的贡献不同,所以ζ增加至5%时,双向轴力的σ仅下降约5%~7%,而MX的σ下降约25%。 (4)共振分量σR随风速V的增加有两方面的原因,荷载频谱趋向高频而导致的σR的增加,以及荷载幅值增加使各响应分量的增加。仅计第一个原因时,各响应σR基本随V(或时间比λT)呈线性增加,所以同时考虑两方面的原因时σR与V3成正比。 (5)子午向相关性主要是通过σB而影响σ,并且主要对双向轴力的σ有影响。这也是由于双向轴力的σ均以σB为主,子午向相关性的提高使FY的σ有所增加但使FX的σ有所增减小,这可通过内力影响面得以验证。对于环向弯矩MX,由于其σB相对偏小,且受子午向相关性影响不大,所以子午向相关性对MX的σ影响亦不明显。2.2 阻尼比ζ的影响
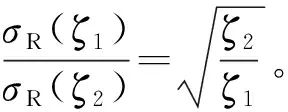
2.3 风速取值V的影响
2.4 风压相关性的影响
3 结 论
