基于自适应序贯相似性检测波形匹配延拓的EMD端点效应抑制

杨剑锋， 石戈戈， 周天奇， 高锋阳

(1. 兰州交通大学 自动化与电气工程学院，兰州 730070； 2. 兰州交通大学 光电技术与智能控制教育部重点实验室，兰州 730070)

经验模态分解(Empirical Mode Decomposition，EMD)自Huang等[1-2]提出后，由于其在处理非线性、非平稳性信号方面的优越特性，在工程实践和研究领域得到了快速发展。由于该算法相关理论还有待完善，所以在数据分解过程中出现了一些问题，端点效应就是其中很重要的一个[3]，严重影响了结果的准确性和有效性。针对此问题，前后有许多研究人员致力于端点效应抑制算法的研究。其间有很多端点效应抑制算法被提出，由于基于波形匹配的端点延拓算法[4]不仅考虑了端点处的数据变化趋势同时还考虑到了原始波形内部的数据变化，具有很好的端点效应抑制效果，特别在信号规律性较强的情况下，所以在EMD端点效应的抑制方面得到了广泛的应用。波形匹配延拓法抑制端点效应效果的好坏很大程度上取决于波形匹配的精确度和效率，针对此种情况，本文提出了基于自适应序贯相似检测波形匹配延拓的端点效应抑制方法。

1 端点效应及抑制方法

Huang等认为每个复杂的振动均是由若干个单一模态的振动叠加而成，基于这个基本理念，提出了固有模态函数(Intrinsic Mode Function，IMF)的概念和EMD的基本原理。EMD过程实际上就是通过信号极值点，形成上、下包络，再通过反复筛选，按高阶分量到低阶分量的顺序，分解出IMF的过程。正是借助于EMD过程，才使分解得到的IMF在做Hilbert变换后得到的瞬时频率具有物理意义。

由于EMD分解时须对极值点进行三次样条插值形成包络线。但是信号的端点往往并不是极值点，导致在端点处形成包络时出现下包络超越上包络，一部分信号处于上、下包络之外的情况，最终导致端点处的波形失真[5]。如果待处理的信号时间尺度大或信号短时，失真现象还会向中间部分延伸，造成最终的IMF准确性受到很大影响，严重时甚至会使最终分解出的IMF失去其意义，这种现象被称为端点效应[6-7]。

近年来，国内学者通过深入学习和研究提出了不少算法来抑制端点效应在信号EMD分解过程中带来的不良影响。典型的有Huang等提出的特征波法；文献[8]所提的镜像闭合延拓法，该方法依据的是在左右对称的极值点处采用镜像原理使原始信号对称延长为原信号的两倍，延长后的信号首尾相接后便形成了一个闭环，消除了端点，也就消除了端点效应[9]。这种方法直观性强，操作也简单，但是对信号本身的对称性要求高，在处理对称性不强的信号时，容易产生误差。2010年，Wu等[10]提出了一种新颖的基于数学模型的比例延拓法，该算法计算和原理均简单，在处理端点效应上的效果也很好，但在有些情况下满足不了极大值和极小值交错的条件。此外，还有多项式拟合法等[11-12]。随着人工智能的兴起，基于人工智能的算法也陆续被提出，比较典型的有人工神经网络法(Artificial Neural Network，ANN)[13]和支持向量机回归法(Support Vector Regression，SVR)[14]，ANN经过大量的数据训练，可以处理复杂的非线性数据，抑制端点效应产生，但是算法本身复杂，计算和训练耗时长。SVR具有泛化能力好等优点，但是在选取最优核函数和模型参数时仍然存在问题。

2 自适应序贯相似性检测波形匹配延拓

在端点效应抑制方面常用的一种算法还有波形匹配延拓法，该算法依据的理念是信号的变化趋势除了在端点处有所表现外，信号内部也有表现，尤其是规律性较强的信号[15]。具体的操作流程主要包含两个部分：①在信号内部寻找与端点处变化趋势最为吻合的一段子波；②将匹配最佳的子波平移到端点处进行延拓。该算法由于其端点效应抑制效果的优越，尤其在针对规律性较强的信号的端点效应处理方面得到了广泛的应用。其最佳匹配子波的寻找算法是研究该算法的关键和热点。针对此问题，本文提出了一种基于自适应序贯相似性检测波形匹配延拓的EMD端点效应抑制方法。

序贯分析这一概念来源于数理统计，其名称出自瓦尔德的一本同名著作，其主要的研究方向是序贯抽样方案并用此种方案进行统计推断。其主要思想是在抽取样本的过程中并不事先确定所需样本个数，而是先抽取一小部分，再根据这一小部分样本的结果决定是否进行继续抽样工作，从而有效降低抽样个数。

序贯相似性检测算法由于其计算量低，精度高的优点，在图像匹配等领域得到了广泛应用。其性能的主要影响因素是阈值的选取及其调整策略。

以往截止阈值的定义一般直接采用匹配子波和待匹配子波幅值差的绝对值或平方形式，并不考虑匹配子波的幅值，这样做的不足之处就是很难直观反映出两者的匹配精度，不利于阈值的选取。所以在本文中采用的是差值除以原始子波极大值减去极小值再平方的方式，让单纯的匹配误差转化为具有统一标准的匹配精度误差，提高直观性和降低因阈值选取而引入的误差。同时，在截止阈值调整过程中采用何种策略对于计算量有很大影响，本文以对折的自适应方式调节截止阈值，可以用最快的速率遍历每个待匹配子波，用最少的时间选出最佳匹配子波。而且相对于通常均匀调整的方式，由于对折方式的收缩速度更快，所以还可减少初始阈值选取带来的的计算量影响，增加算法性能的稳定性。通过重复上述步骤，最终选取出最佳匹配波形，再经过平移进行端点延拓。

其具体操作步骤如下：

步骤1确定端点处的原始子波X，为了能较好的反映端点处波形的变化趋势，选取的原始子波应包含一个极大值点和极小值点，纵坐标分别记为M和m，对原始子波进行采样，得到K个采样点值；

步骤2对原始信号进行采样，并形成若干与原始子波长度相等的待匹配子波库Y；

步骤3选择初始截止阈值T1；

步骤6重复上述步骤，选出初始截止阈值下的若干种子波形；

步骤7若上述步骤选出的种子波形的数量N≥2时，减小截止阈值，重复上述步骤。N=0时，则增大截止阈值，重复步骤1～步骤5直到能选出种子子波；

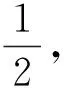
步骤9重复步骤1～步骤8，直到选出的种子波形数量为1，该子波记为最佳匹配波形；

步骤10分别选出左右两端的最佳匹配波形后，平移完成端点延拓。

3 模拟信号仿真分析

为了验证算法的有效性，本文引用了一个非线性的调幅调频信号，其表达式为

y(t)=(1+0.15 sin(2π×7.5t))cos(2π×30t+
0.6×sin(2π×15t))+sin(2π×120t)

(1)

式中： 采样频率为3 000 Hz，采样点数为600，为了便于观察算法结果的对比，下面给出了信号的组成分量和合成信号(见图1)。

图1 信号组成及合成信号Fig.1 Signal components and synthetic signal

图2为没有进行端点处理直接进行EMD得到的各个IMF分量及其余量，图3为相应的Hilbert谱，由图2和图3可知，在没有进行任何端点处理的情况下直接进行EMD会产生严重的端点效应同时还产生了一个虚假固有模态分量。

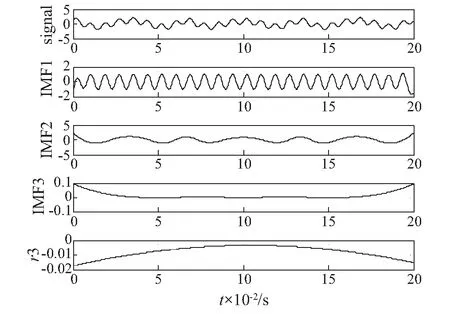
图2 原信号EMD结果Fig.2 EMD result of original signal

图3 原信号EMD结果的Hilbert谱Fig.3 Hilbert spectrum of original EMD result

为了验证算法延拓的波形是否符合原信号的发展趋势，本文将原信号左右两端各自截去了50个采样点的长度，再通过算法在信号两端分别进行延拓，通过延拓后信号与原信号的对比来验证算法准确性。图4中，实线为未截取的信号，虚线部分为采用自适应序贯相似性检测波形匹配延拓的信号。由图4可知，采用自适应序贯相似性检测波形匹配延拓的信号与原信号的相似度很高，表明本文算法具有很好的准确性。

图4 原信号与延拓后信号对比Fig.4 Contrast between extension result and original signal

图5和图6分别为采用本文算法处理后的EMD结果和相应的Hilbert谱，由图5和图6可知，经过本文算法处理，IMF分量的Hilbert谱端点处的波动明显降低很多同时还减少了一个伪分量，表明了本文算法对EMD过程中的端点效应有很好的抑制效果。

图5 延拓后EMD结果Fig.5 EMD result after extension

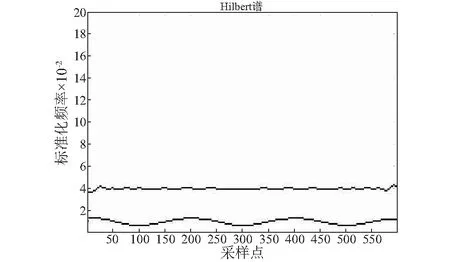
图6 本文算法延拓后EMD结果的Hilbert谱Fig.6 Hilbert spectrum of proposed algorithm EMD result after extension

图7和图8分别为未经端点处理的信号直接进行EMD和几种常见的端点效应抑制方法处理后EMD产生的IMF1和IMF2和原信号高频和低频分量的对比。其中，虚线表示未进行处理直接进行EMD结果；点线表示镜像延拓处理后的EMD结果;实线表示经过本文算法处理后EMD结果；点画线表示经过多项式拟合法处理后EMD结果；星形线表示原信号的原始分量；由以上对比图可以清晰看到经过端点处理分解出的IMF分量较之未经处理直接分解出的IMF分量，与原始分量更为相似，直观上看，其中实线波形较之点线和点画线波形，与星形线波形更为贴近。同时，通过调用MATLAB命令分别计算不同处理方法产生的IMF分量和与之相对应的原始信号分量之间的相关系数，结果也说明了本文算法对EMD过程中的端点效应有相对更好的抑制效果。各种算法EMD结果与原始信号的相似度，如表1所示。

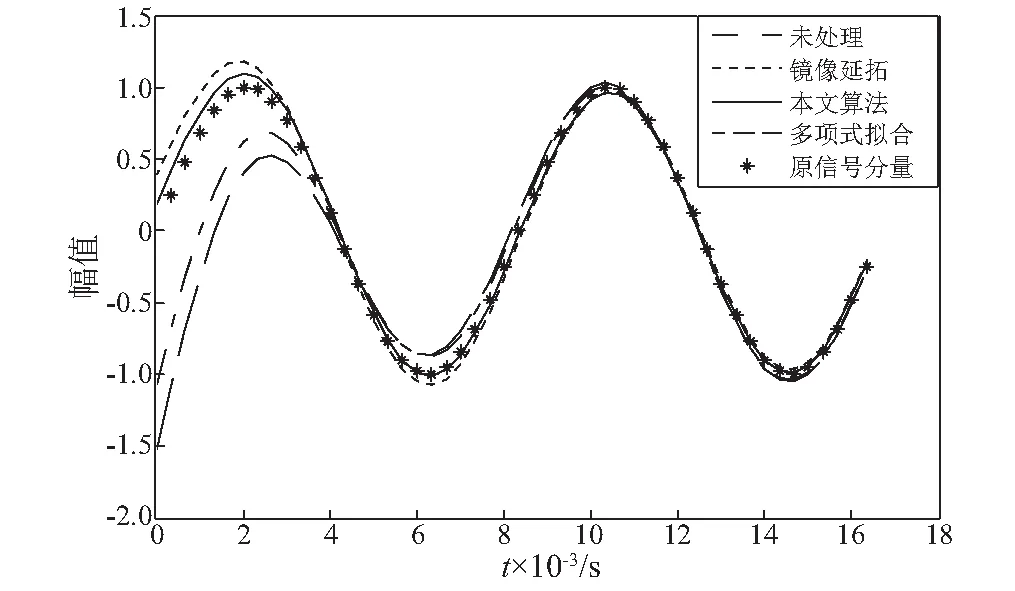
图7 各种延拓方法EMD结果和原始正弦分量信号对比Fig.7 Contrast between original sine signal and EMD result of different extension methods

图8 各种延拓方法和原始调幅信号对比Fig.8 Contrast between original amplitude modulated signal and EMD result of different extension methods

直接分解法镜像延拓法本文算法多项式拟合法ρ-IMF10.933 40.995 10.998 30.993 5ρ-IMF20.926 50.994 90.997 60.994 6

4 实际信号分析

为了进一步验证算法的有效性，本文选取了一段来自于美国凯斯西储大学的电机驱动端振动加速度数据来进行分析，如图9所示。直接进行EMD和采取本文算法进行端点处理后再进行EMD的两种情况分别进行仿真对比。由图10可知，直接进行EMD会在IMF分量两端出现较为严重的端点效应；由图11的分解结果可以看出采用本文算法进行端点延拓后再进行EMD可以很好的抑制端点效应。

图9 电机驱动端振动加速度信号Fig.9 Accelerometer data of motor drive end

图10 振动加速度信号EMD结果Fig.10 EMD result of drive end accelerometer data

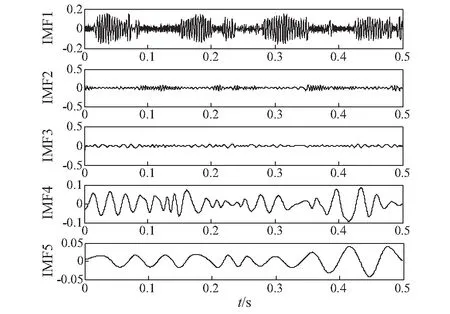
图11 本文算法处理后EMD结果Fig.11 EMD result of proposed algorithm

5 结 论

针对EMD过程中出现的端点效应问题，本文在分析端点效应产生原因的基础上，提出了一种基于自适应序贯相似性检测波形匹配延拓的EMD端点效应抑制方法。并对其进行了仿真对比分析，验证了该算法在抑制EMD过程中的端点效应具有很好的效果，并且该算法准确性高，稳健性强，匹配速度快，同时具有较强的通用性。但由于该算法是基于波形延拓的，所以对信号的规律性有一定要求，这也在一定程度上限制了它的应用。同时，在选取最佳原始子波长度等问题上也还需进一步讨论。