线性调频雷达移频卷积调制干扰技术仿真分析∗

徐 鹏 刘东青 马攀伟

（空军预警学院 武汉 430019）

1 引言

现代雷达技术发展日新月异，其抗干扰能力也越来越强，特别是大时宽、大带宽的线性调频（Linear Frequency Modulation，LFM）信号对干扰机的干扰样式提出了更高的要求［1～2］。脉冲压缩技术解决了雷达探测距离和距离分辨力之间的矛盾［3］，该技术在多种型号的雷达中得到了广泛的应用。脉冲压缩体制雷达既具有窄脉冲的高距离分辨力，又可获得宽脉冲的大探测距离，而且使得耦合度不高的信号难以获得雷达接收机的增益，大大增强了雷达抗干扰能力。

随着数字射频存储器［4］（Digital Radio Frequency Memory，DRFM）的运用和和发展，结合先进的雷达信号分析处理技术，特别是大规模、高速、高效的集成电路的发展，使得对于雷达射频信号的快速采集、复制、存储已经不再困难，而且干扰机能够产生与雷达接收机耦合度极高的干扰信号，使得雷达的抗干扰能力大大降低。移频干扰［5］就是随着DRFM的发展而来的具有高耦合度的干扰样式，移频干扰能够获得雷达接收机的相干增益，在距离上产生虚假目标。移频干扰也就成为目前阶段研究干扰和抗干扰技术不得不提的一种干扰样式。

文献［6～7］中研究的抗移频干扰方法能够有效地识别由固定移频干扰产生的距离假目标，使得雷达能够在固定移频干扰下保持正常工作。为了解决固定移频干扰的局限性，论文结合卷积调制干扰［8］，提出了一种组合型的干扰样式，在固定移频干扰的基础上叠加卷积调制干扰的方法。文中采用了锯齿波卷积调制方式并通过多次Matlab仿真实验［9］，对比分析实验数据，本方法能够对真实目标产生有效的压制和欺骗干扰。

2 线性调频信号移频干扰原理

LFM信号的数学表达式［10］：

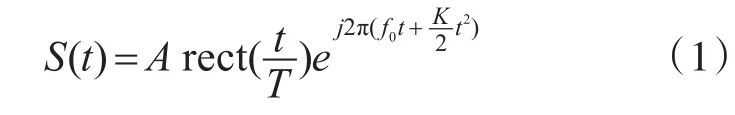
其中A为信号幅度，f0为载波频率，T为脉冲宽度，为调制斜率，B为调制带宽。LFM信号的频谱特性与矩形函数十分接近，频谱宽度近似为信号的调制带宽B，而且其相位具有平方率特性。

LFM信号的模糊函数表达式如下：

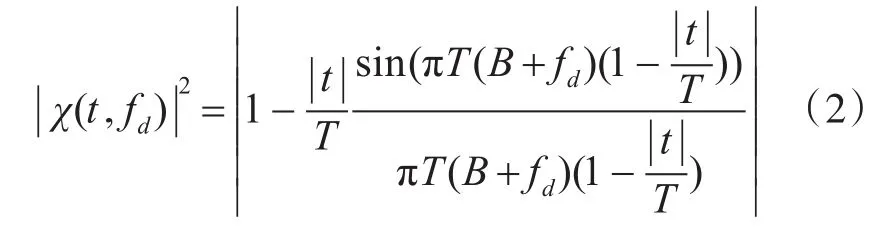
其模糊函数图如图1所示，在其二维联合参数估计中，时间延时t和移频量 fd之间具有很强的耦合性，即频移量Δf变化，随之在时域上的时延也会变化Δt，那么将接收到的雷达信号经复制后，移频转发出去就会在距离上产生假目标干扰。

图1 LFM信号模糊函数图

由傅里叶变换性质可知：

即频域移频相当于在时域信号的基础上增加一项e-j2πfct的频率调制系数。则增加移频后的干扰时域表达式为

经过t0的延时，目标回波时域表达式为

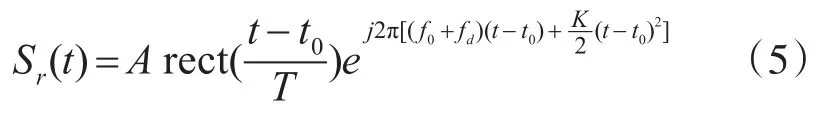
加入固定频移的干扰时域表达式为

上式（5）、（6）中 t0为回波延时，fd为目标的多普勒速度，ξ为固定移频的频移量。为了方便分析取h(t)=S*(-t)，则目标回波信号经过匹配滤波器的输出为

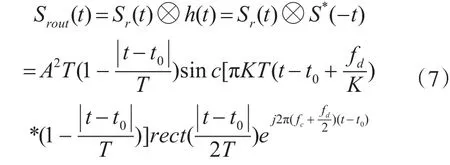
同理干扰信号经过匹配滤波器输出：

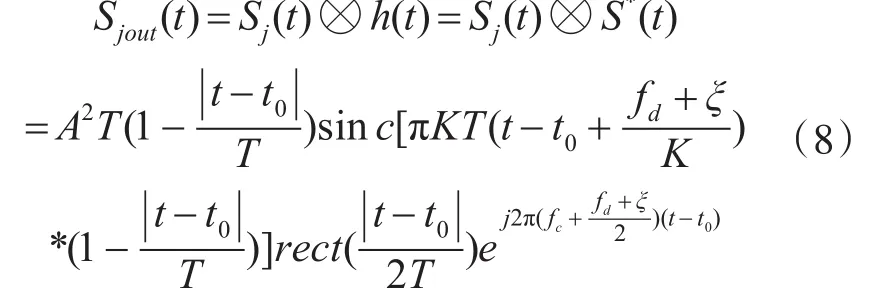
由上（7）、（8）可知，目标回波信号经匹配滤波后最大峰值在时刻出现，而干扰信号峰值则在时刻出现，这就相当于当ξ＞0时，产生近距假目标，当ξ＜0时，产生远距假目标。

目标回波信号和固定移频干扰信号一起经过匹配滤波器的输出结果如图2所示，其中设置t0=0，fd=0 ，信号幅度 A=1，载波频率为1GHz，脉冲宽度为10us，调制带宽为10MHz，采样频率为40MHz，干扰信号移频量分别为-2MHz和3MHz，幅度进行归一化。

图2 固定移频干扰脉冲压缩

由仿真图可以看出线性调频信号具有强耦合性，经过脉冲压缩后形成一个较高的主峰，有利于雷达对真实目标信号的检测与识别。单一固定移频干扰经过脉冲压缩形成一个主瓣，且移频量越大，干扰信号幅值越低，理论上移频量在(-B/2，B/2)之间，否则将没有干扰效果。而且可以发现干扰移频量越大，干扰信号距离真目标的距离就越远，这与之前的理论分析是一致的。

3 卷积调制干扰原理

设雷达射频信号为S(t)，干扰机发射信号为Jr(t)，干扰机将接收到的雷达发射脉冲与存储在DRFM内的调制信号p(t)相卷积来产生干扰信号，数学过程为

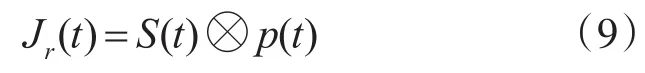
经功率放大后由干扰机发射出去。所以雷达接收机收到的回波信号中包含目标信号和干扰信号，回波信号可以表示为

经匹配滤波器后输出为

其中S*(t)为S(t)的共轭。

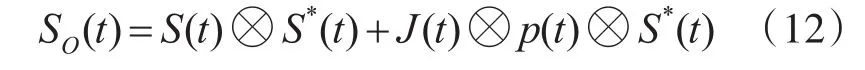
把式（9）代入式（11）中展开后得：将上式时域卷积转化为频域乘积的形式，设SO(f)，S(f)，p(f)分别为 SO(t)，S(t)，p(t)的频谱，所以有

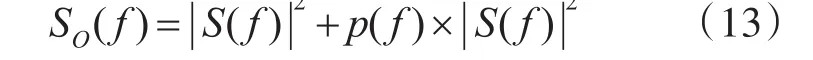
再进行傅里叶逆变换：

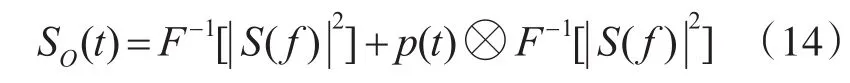
4 仿真实验分析

随着现代雷达抗干扰技术的发展，固定移频干扰产生的假目标已经能够被雷达通过距离补偿所识别，考虑到固定移频干扰只能产生单个的距离假目标干扰，干扰样式比较单一，而且不能对雷达真实的目标回波信号进行覆盖，所以在移频干扰的基础上提出一种叠加卷积调制干扰的干扰方法，由于篇幅限制，论文主要就固定移频叠加锯齿波脉冲串卷积调制干扰的干扰样式进行仿真分析和研究，验证这种新的干扰样式的正确性和有效性。固定移频叠加锯齿波脉冲串卷积调制干扰实际工作过程为干扰机先对接收到的雷达射频信号进行分析保存，经过固定移频后再与机内产生的锯齿波脉冲串进行时域卷积后转发出去。

仿真实验图如图3所示，锯齿波脉冲串的数量分别为10个和20个，固定移频干扰移频量分别为2MHz和4MHz，其他基本参数设置和图2一致，对图形进行归一化处理。

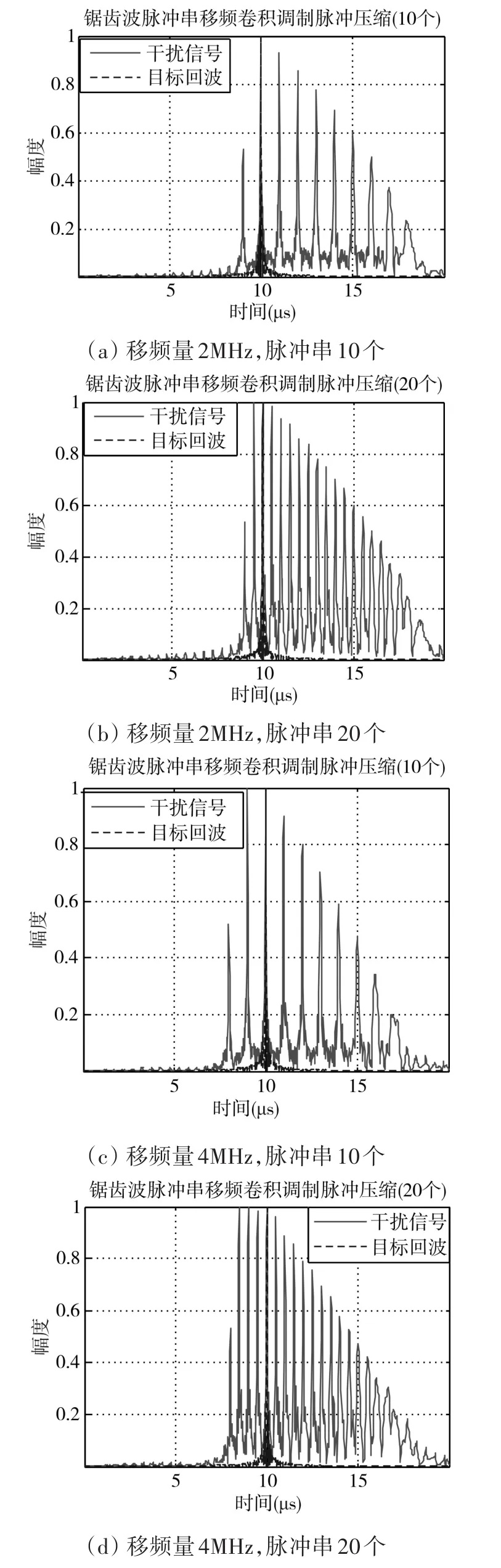
图3 移频卷积调制干扰仿真图

由图3中（a）和（b）对比发现，锯齿波脉冲串的数量实际决定了干扰信号脉冲数，锯齿波脉冲串的数量越多则干扰脉冲数越多，该干扰样式在不同距离上形成了多个干扰脉冲，产生了距离欺骗干扰，干扰效果要远好于固定移频干扰。对比图3中（b）和（d）可知，移频量决定干扰的最左侧旁瓣与真实目标之间的距离差，锯齿波脉冲串的数量越多，干扰信号旁瓣之间的距离也就越小，当用来调制的锯齿波脉冲串数量足够多时，就会对真实目标产生压制性干扰。根据雷达的实际情况及时调整脉冲串数量和固定移频干扰的移频量可以使干扰效果达到最佳。

5 结语

论文针对大时宽带宽积的线性调频雷达，分析了移频干扰和时域卷积调制干扰的原理，在此基础上给出了一种组合型的新的干扰样式。通过仿真实验，分别比较分析了移频量、锯齿波脉冲串数量对线性调频信号干扰效果的影响。组合型干扰样式的干扰效果明显好于传统的移频干扰。在实际作战过程中，采用适当的移频量和调制脉冲串数，可以对真实目标产生压制和欺骗干扰，具有一定的实战价值。