分布式电源接入微电网电能质量控制研究∗

王晓明 马 喆 薛亚龙

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）（2.甘肃建苑建筑设计院有限公司 兰州 730050）

1 引言

分布式电源（DG）因其占地少、投资少、见效快、调峰方便、灵活性高、清洁环保等优点，已成为新世纪电力产业的重要发展方向之一［1］。分布式电源接入微电网会改变微电网的结构和运行，合理的安装位置和容量可有效改善微电网电压分布、减少系统有功网损、提高线路负载能力等［2］。但如果DG配置不合理，将得不到相应的效果，甚至可能威胁电网安全稳定的运行［3］。为了更好地利用分布式能源，应先解决规划阶段分布式电源的配置问题，即选择合适的安装位置及容量可达到对微电网电能的质量控制。微分进化（DE）算法是一种基于新型进化算法，因其易使用、鲁棒性强和收敛性好，已被广泛应用到实际工程中［4］。为使其适用于多目标优化问题的求解，将NSGA-II中pareto等级和拥挤距离排序操作引入DE算法中，提出了多目标差分进化算法（DEMO）。然而，DEMO算法中参与变异操作的个体完全来自于随机选择，存在选择压力小，收敛慢的不足，并且交叉、变异操作对参数依赖性强，其固定的参数设置不具备普适性［5］。针对DEMO存在的问题，本文引入差分排名变异算子和控制参数自适应调整策略操作，并用其求解以降低微电网网损、提高微电网电压质量和电压稳定性为目标的多目标优化配置模型。对求得的pareto最优解集，使用灰色关联决策模型对其进行决策从而得到最终方案。以IEEE-33节点系统为算例验证所提方法的有效性。

2 数学模型

2.1 目标函数

电力系统运行的基本要求是能够保证可靠的持续供电、具备良好的电能质量和运行的经济性。依据以上要求，本文以降低微电网网损、提高微电网电压质量和电压稳定性为目标，建立了多目标优化配置模型。

1）微电网网络损耗

网损是衡量微电网运行经济性的一项重要指标，系统有功损耗的数学表达式可以表示为

其中，B是系统支路总数；Gk是连接节点i和 j的支路k的电导；V和θ分别是节点电压幅值和相位。

2）节点电压偏差

DG能有效改善微电网中节点电压的分布情况，各节点与系统正常电压值偏差的均值可用来表征系统的电压偏差，其数学表达式为

其中，ΔU是节点电压偏移值；N是微电网系统的节点总数；Ui表示DG接入后节点i的电压幅值；Uir表示微电系统节点i额定电压幅值，其值为1.0p.u。

3）静态电压稳定性指标

DG的接入对微电网电压稳定水平有很大的影响，合理地规划DG可以有效地改善电压稳定水平，保证系统更加稳定的运行。通常用静态电压稳定指标（VSI）来表征系统电压稳定性［6］。对于支路k，有

其中，Rij和Xij分别是支路k的电阻和电抗；Pj和Qj分别是支路k的接收端点 j的有功功率和无功功率。全系统的静态电压稳定指标VSI取所有支路中的最大静态电压稳定指标，即VSI=max{VSIi|i=1，2，…，k}。

在综合考虑微电网系统的经济性、安全性和稳定性后，分布式电源的多目标函数为

2.2 约束条件

本研究给出如下约束条件：1）假设Pi、PDGi和PLi分别是在节点i处发电机有功出力、DG有功出力和有功负荷；Qi、QDGi和QLi分别是在节点i处发电机无功出力、DG无功出力和无功负荷。则功率平衡为

3 改进微分进化算法

3.1 多目标排名变异算子

差分排名变异算子对整个DE种群按目标函数值从优到劣进行排序，优秀的个体以较大的选择概率参与变异，而低劣的个体以较小的选择概率参与变异［7］。考虑到DEMO算法采用的是DE/rand/l变异算子，参与变异操作的个体完全来自于随机选择，存在选择压力小，收敛慢的不足［8］，本文将差分排名变异算子引入到多目标差分进化算法中。对整个种群进行优劣排序后，分配每个个体的排名值，优劣顺序为第i的排名值为

因此，越优秀的个体被赋予越大的排名值。越优秀的个体被选中的概率越大，排在第i位的个体的被选择的概率为

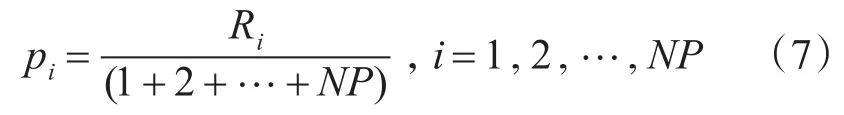
3.2 控制参数自适应调整

DEMO算法的变异因子F和交叉因子CR的取值对算法的收敛速度及稳定性有很大影响［9］。本文提出了变异因子F和交叉因子CR自适应取值策略：

其中，Ri为个体排名值，NP为种群个数，Fmax和Fmin分别为F上下限，CRmax和CRmin分别为CR的上下限。

4 多属性决策方法

4.1 灰色关联法

灰色关联分析法对样本量的多少和样本有无规律无特别要求，而且计算量小，实现方便，更不会出现量化结果与定性结果不符的情况［10］。灰色关联分析综合评价的基本步骤如下：

1）确定比较序列和参考序列

有m个待评估方案，每个方案有n项指标，xij代表第i个方案的第 j个指标值，则m个方案的全部指标构成评估矩阵 X=(xij)m×n。为消除各变量的量纲效应，采用标准0～1变换对待评估矩阵进行标准化处理。设第i个评估点的第 j个指标值规范化后为 rij，Xmax，j和 Xmin，j分别为所有样本中第j个指标的最大和最小值。

当指标为正指标时，即指标值越大越好，指标的标准化公式为

当指标为逆指标时，即指标值越小越好，指标的标准化公式为

待评估矩阵x经标准化处理后得到矩阵R=(rij)m×n，即比较序列。本文取其矩阵R中每个指 标 的 最 优 值组 成 理 想 方 案即为参考序列。

2）计算关联系数

关联系数εij是待评估方案序列曲线i与理想方案序列曲线在指标 j的相对差值，其计算公式为

其中，ρ为分辨系数，ρ∈[0，1]，计算可得到各方案与理想方案在全部指标上的关联系数矩阵ε=(εij)m×n。

3）计算灰色关联度

第i个评价方案与理想方案的关联度为

其中，ωj为第 j个指标的权重。

4.2 博弈论组合

采用基于组合权重的灰色关联分析法评估DG安装备选方案的关键在于指标的权重的选取，其取值直接关乎到评估结果的科学合理性［11］。客观权重体现了属性的信息量，主观权重体现了属性的价值量，主客观权重的组合实现了信息量和价值量的统一。本文采用基于博弈论的组合赋权法来确定各指标的权重［12］。用L种方法对指标分别赋权，得到 权 重 集， 其 中k=1，2，…，L。由L种权重向量组成的权重向量集为 W=(ω1，ω2，…，ωn)，则 L 个权重向量的任意线性组合为

其中，ωk为第k种赋权法求出的权重向量，∂k为线性组合系数。根据博弈论组合赋权思想，要寻找最优权重向量，即ω*与权重向量集W中各权重向量离差极小化的线性组合系数，由矩阵的微分性质可得最优化一阶导数条件：

求解方程可得到线性组合系数 (∂1，∂2，…，∂L)，进而得到最终的组合权重为

5 实验分析

5.1 实验准备

为了验证本文模型和算法的合理性与正确性，选用IEEE-33节点微电系统，为其进行分布式电源位置和容量的规划。IEEE33节点微电测试系统如图1所示。

图1 IEEE-33节点微电系统

该微电系统有37条普通支路，14条运算支路，33个节点，首节点（0）为平衡节点，首端基准电压为12.66kV，三相功率准值取10MVA，总负荷为3.175MW+2.3Mvar。假设节点电压取值范围为0.9p.u～1.05p.u ，DG待选安装节点编号为1～32，共32个，最大DG安装节点数为3个，最大安装总容量为2MW，功率因数恒为1。算法参数设置如下：种群规模NP=100；最大迭代次数K=150；变异因子上限为0.8，下限为0.3；交叉因子上限为0.8，下限为0.3。

5.2 性能评估

为验证本文算法的有效性，还采用NSGA-II［13］和DEMO［14］对模型进行求解，并对结果进行对比。各算法独立进行30次运算。对于各个目标函数，每个算法在每代可得到30个外部解。统计各算法30次运算后得到的外部解对应的目标分量平均值，并绘制电压稳定性、微电网损耗和电压偏差外部解进化曲线分别如图2、图3和图4所示。

图2 电压稳定性

图3 微电网损耗

图4 电压偏差外部解

可以看出，改进DEMO在收敛速度和深度上有更好的表现。特别是在网损目标和电压偏差目标上，改进DEMO的优势相对于NSGA-II和DEMO较为明显。外部解比较是对pareto解集中的特殊解的比较，虽然能较为直接反映算法的收敛性能，但具有一定的片面性。为更全面地比较各算法的收敛性能，引入C指标进一步分析。C指标用于描述两个解集相对质量的高低，对于2个解集Q1和指标的计算公式为［15］

其中，用于衡量Q2中有多少比例的解被Q1中的解支配。各算法独立运行30次，统计两两之间最终代C指标的平均值，如表1所示。

表1 指标平均值

从表1可以看出，DEMO和改进DEMO得到的解分别支配了36%和42%的NSGA-II的解，远大于它们被NSGA-II支配的解，即同等条件下DEMO算法和改进DEMO算法解集的质量高于NSGA-II。而改进DEMO支配了20%DEMO的解，其被DEMO支配的解的比例为11%，即改进DEMO解集的质量相对DEMO有一定的提高。

5.3 方案选取

首先按照指标格式对决策矩阵规范化；然后使用熵权法确定各属性的客观权重，求得网损、电压偏差和静态电压稳定性指标的客观权重为w1=(0.3511，0.5063，0.1426)利用模糊赋权法求主观权重，选择3名专家对3个属性重要程度进行评分，得到主观权重：w2=(0.4960，0.3664，0.1376)；运用博弈论求解组合权重的方法计算得到组合权重w=(0.4218，0.4380，0.1402)；最后利用灰色关联分析法计算各备选方案与理想方案关联度，选取关联度最大的作为优选方案。为了体现不同优化方案对电网的影响，本文选取以下5个方案进行比较：

方案1：未接入分布式电源；

方案2：在pareto前沿中，系统网损最小对应的优化方案；

方案3：在pareto前沿中，系统节点偏差最小对应的优化方案；

方案4：在pareto前沿中，系统静态电压稳定性最小对应的优化方案；

方案5：在pareto前沿中，基于组合权重和灰色关联分析法得到的优化方案。

针对这5个方案对应的DG安装节点位置、容量和电网评价指标如表2所示。

表2 不同DG规划比较

表2是DG优化配置的几种典型方案。其中，方案2的系统网损更接近最小值，但电压偏差更接近最大值，有利于微电网运行的经济性，但就电压质量的提升远不如其他方案。方案3具有较小的电压偏差，但系统网损和静态电压稳定性指标较大，较适用于对电压质量要求高的情况。方案4静态电压稳定性指标达到了最小，并且系统网损也有了较大的改善，但电压质量的提升不够明显。方案5为综合考虑各指标的重要程度和DG并网后对微电网影响程度后，使用灰色关联分析法选出的综合最优方案，对静态电压稳定性指标的减小几乎与方案4一样，对电压偏差的改善虽然不如方案3，但远优于方案2和4，并且较好地降低了网损，很好地协调各个子目标的关系。这体现了本文决策技术的优越性，选择的合理性。

6 结语

结合微电网系统运行的基本要求，选用网损、电压偏差和电压稳定性3个指标，建立了DG多目标选址定容问题的数学模型，算例结果表明该模型能够很好地评估DG接入微电网系统所带来的电能质量控制影响。对DEMO算法进行了改进，引入差分排名变异算子增加优秀个体参与变异操作的概率，以加强算法的收敛速度以及搜索成功率；采用控制参数自适应调整策略解决算法对控制参数依赖性强的问题。通过与DEMO和NSGA-II算法比较，证明了在求解DG多目标选址定容问题的数学模型上，改进策略具备可行性。应用灰色关联分析法对pareto解集进行排序，结果验证了该方法能够较好地协调各个目标，实现DG多目标选址定容的决策功能。