为数学点赞——名师例数学文化（7）三角学的发展简史及三个历史名题的证明

■北京市教育学院丰台分院 张 琦

■北京市第十二中学高中部 高慧明

本刊特邀栏目专家简介:

高慧明 首届全国十佳班主任,全国著名数学特级教师,国家教育部课程改革“全国先进工作者”,全国著名高考数学命题与考试研究专家,国家教育部“国培计划”全国中小学教师培训、班主任培训、校长培训特邀主讲专家,受邀在全国各地做有关高考科学备考、班级管理等多场专题报告。现任教于北京市第十二中学高中部。

三角学的英文名称是Trigonometry,来自拉丁文Trigonometria,实际上是trigono(三角)和metrein(测量)的组合。其原意为三角形测量,是以研究平面三角形和球面三角形的边与角的关系为基础的一门数学学科。早期的三角学是天文学的一部分,后来研究范围逐渐扩大,变成以三角函数为主要对象的学科。现在,三角学的研究范围已不仅限于三角形,且为数理分析之基础,研究实用科学所必需之工具。

一、三角学的萌芽与初步发展

约成书于公元前1650年的《莱因德纸草书》可以看作是早期三角学的萌芽。《莱因德纸草书》中的第56～60题是金字塔问题,题目的内容都围绕金字塔展开。从中可看到三角学的初步知识。

例如第56题:一个金字塔(正四棱锥),高是250cubit,底面边长是360cubit,求seked值。(注:古埃及人将一倾斜直线每垂直升高一个单位时,相对下垂线的水平偏离称之为“seked”,亦即底边的一半与高之比,相当于底角的余切值。)

古希腊的数学家泰勒斯(Thales,前624—前547)提出并证明了以下几何命题:“等腰三角形两底角相等;相似三角形的各对应边成比例;若两三角形两角和一边对应相等,则两三角形全等”。这些定理是现代每一个中学生都知道的,它们简单得不能再简单了。但是,就是这些简单的理论,构成了今天极其复杂而又高深的理论的根基。

大多数数学史学家通常认为三角学兴起的标志性人物是古希腊天文学家、数学家希帕霍斯(Hipparchus,约前180—前125?)。早在公元前300年,古埃及人就已有了一定的三角学知识,为了在尼罗河畔谋生存,聪明的古埃及人很早就学会了计算。他们可以准确推算出尼罗河泛滥的日期;河水退落后,他们重新丈量土地、划分地界,并能计算出土地面积;在建造金字塔、神庙、房屋等建筑和分配实物领域,同样也离不开数学;在计算时间、测量距离、付给劳役者报酬、修凿运河、兴建大规模的水利工程等方面也是如此。公元前2世纪后古希腊天文学家希帕霍斯为了天文观测的需要,作了一个和现在三角函数表相仿的“弦表”,不过希帕霍斯的原著已经遗失,因此关于有明确记载的三角学的文献就是古代最有影响的天文学著作——托勒密的《天文学大成》,在该著作中,有一张表被视为最早的正弦表(据信是根据希帕霍斯弦表改编的)。

图1

托勒密在构造弦表时的基本原理如下所示:把圆周分为360等份(他没有用“度”这个概念),把半径长度分为60等份(即直径为120等份),用弧去度量角,用直径的若干等份度量任一圆心角所对长弦的长度,并以符号crd α表示圆心角α所对的弦长。如图1所示,半径OA为60单位,crd α=弦AB之长,crd 2α=弦AC之长。一些特殊角的弦长是不难求的,例如60°,90°,72°,36°的弦长就是圆内接正六边形,圆内接正方形,圆内接正五边形,圆内接正十边形的边长。由于60°的弧所对应的弦长是正六边形的边长,而正六边形的边长等于其外接圆的半径。因此60°的弧所对应的弦长为60个单位,也就意味着30°对应的弦长为30个单位,用现在语言描述也就是sin30°=。

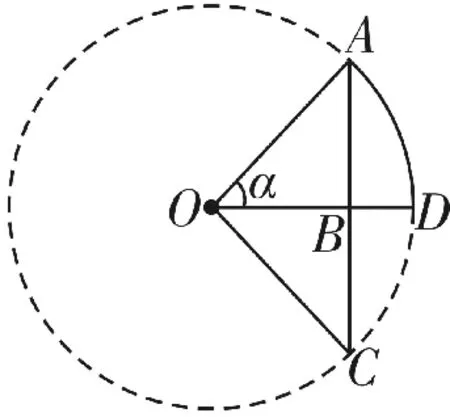
图2

公元5—6世纪,印度的阿耶波多(476—550)采用半弦长来定义正弦,如图2,把半弦AB与全弦所对弧的一半相对应,正弦即半弧所对的半弦AB。当时人们为了应用的方便,已制作出一些不同于早期的弦表。后来,阿拉伯人也采用了印度人的半弦法制作弦表,只不过是加大了圆的半径,制作出精确度更高的弦表。

二、三角学的成熟与发展

三角学从天文学中独立出来的标志是德国数学家雷格蒙塔努斯(1436—1476)于1464年出版《论各种三角形》,这部著作采用印度人的正弦,即圆弧的半弦,明确使用了正弦函数的概念,对三角学做出了完整、独立的阐述。后来,哥白尼的学生雷提库斯(1514—1576)将传统的圆中的弧与弦的关系改进为角的三角函数关系,把三角函数定义为直角三角形的边长之比,从而使平面三角学从球面三角学中独立出来,并定义了六个函数(正弦、余弦、正切、余切、正割、余割)。

雷提库斯具有里程碑式的工作,重点在于考虑∠AOB的正弦是AB,而不是的正弦AB(半弧所对的半弦),如图3。这样,弧的弦变为角的弦,Rt△AOB成为基本结构,而圆成为无关紧要的了。雷提库斯所作正弦概念的小小转变,却使三角函数前进了一大步,雷提库斯把正弦定义为角的三角函数奠定了基础,对后来的三角函数研究产生了极其深刻的影响。

图3

16世纪法国数学家韦达(1540—1603)则更进一步将三角学系统化,他已经对解直角三角形、斜三角形等作出了阐述,并且还有正切定理以及和差化积公式等。至此,三角学从天文学中分离出来,成为数学的一个独立分支。不过,值得注意的是,这时所讨论的“三角函数”仅限于锐角三角函数,而且研究锐角三角函数的目的在于解三角形和三角计算。

三、三角学的历史命题

1.勾股定理的历史

勾股定理是“人类最伟大的十个科学发现之一”,是初等几何中的一个基本定理。这个定理有十分悠久的历史,几乎所有文明古国(希腊、中国、埃及、巴比伦、印度等)对此定理都有所研究。勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯(前572?—前497?)于公元前550年首先发现的。

中国古代对这一数学定理的发现和应用,远比毕达哥拉斯早得多。中国最早的一部数学著作——《周髀算经》的开头,就有一段关于勾三股四弦五的文字,正是勾股定理的一个应用特例。所以现在数学界把它称为“勾股定理”是非常恰当的。

在稍后一点的《九章算术》一书中(约在公元50年至100年间),勾股定理得到了更加规范的一般性表达。书中的《勾股章》说:“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位。尤其是其中体现出来的“形数统一”的思想方法,更具有科学创新的重大意义。

据不完全统计,勾股定理的证明方法已经有400多种了。下面我们向大家介绍几种非常著名的证明方法。

证法1(赵爽证明)：

图4

以a、b 为 直 角 边(b＞a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab。把这四个直角三角形拼成如图4所示的形状。

因为Rt△DAH≌Rt△ABE,所以∠HDA=∠EAB。

因 为 ∠HAD+ ∠HDA=90°,所 以∠EAB+∠HAD=90°。

所以四边形ABCD是一个边长为c的正方形,它的面积等于c2。

因为EF=FG=GH=HE=b-a,∠HEF=90°,所以四边形EFGH是一个边长为b-a的正方形,它的面积等于(b-a)2。

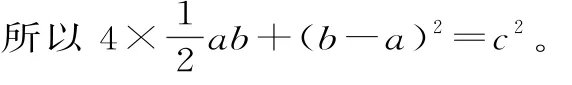
所以a2+b2=c2。

证法2(课本上的证明)：

作8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再作三个边长分别为a、b、c的正方形,把它们像图5那样拼成两个正方形。

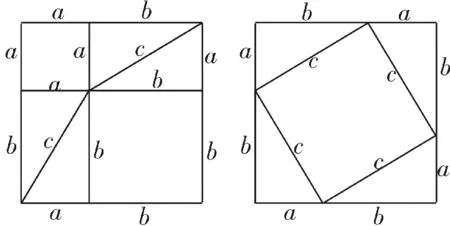
图5

从图上可以看到,这两个正方形的边长都是a+b,所以面积相等。

证法3(1876年美国总统Garfield的证明)：

以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab。把这两个直角三角形拼成如图6所示形状,使A、E、B三点在一条直线上。

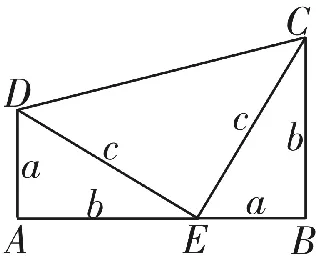
图6

因为 Rt△EAD ≌Rt△CBE,所以∠ADE=∠BEC。

因 为 ∠AED+∠ADE=90°,所以∠AED+∠BEC=90°。

所以∠DEC=180°―90°=90°。

又因为∠DAE=90°,∠EBC=90°,所以AD∥BC。

证法4(欧几里得证明)：

作三个边长分别为a、b、c的正方形,把它们拼成如图7所示形状,使H、C、B三点在一条直线上,连接BF、CD。过C作CL⊥DE,交AB于点M,交DE于点L。

因为AF=AC,AB=AD,∠FAB=∠CAD,所以△FAB≌△CAD。

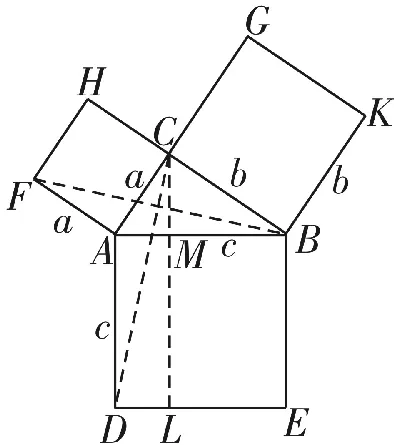
图7

同理可证,矩形MLEB的面积=b2。

因为正方形ADEB的面积=矩形ADLM的面积+矩形MLEB的面积,所以c2=a2+b2,即a2+b2=c2。

2.托勒密定理

古希腊时期的数学家托勒密于公元150年给出并证明了一条关于圆内接四边形的引理,现称为托勒密定理,其内容是:圆内接四边形两组对边之积的和等于两条对角线之积,即AB·CD+BC·DA=AC·BD(如图8)。从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质。

图8

两端乘以外接圆直径的平方d2,并结合正弦定理得:

AB·CD+BC·DA=AC·BD,定理证毕。

3.海伦公式

海伦公式亦称“海伦—秦九韶公式”。此公式(利用三角形的三条边长来求三角形面积)相传是亚历山大港的海伦(10—70)发现的,并可在写于公元60年的《Metrica》中找到证明。也有人认为早于阿基米德时代人类已经懂得这个公式,而由于《Metrica》是一部古代数学知识的结集,该公式的发现时期很有可能先于海伦的著作。