基于多尺度自适应均衡的遥感图像边缘检测方法*

马 鹏， 王小鹏， 张永芳， 麻文刚

(兰州交通大学 电子与信息工程学院，甘肃 兰州 730070)

0 引 言

在利用遥感图像对自然保护区、城市生态和大型区域开发建设的环境进行监察时，识别目标区域是重要步骤之一，而遥感图像中目标的边缘是识别目标的重要特征之一[1]。目前,针对图像的边缘检测已提出了许多方法[2～6]，其中文献[3]改进了Canny算子，采用双边滤波代替传统高斯滤波，通过控制双边滤波器权重参数来减少图像边缘信息的丢失，减少了假边缘，但改进后的算法复杂度较高；文献[4]利用模糊理论的边缘检测算法，将模糊滤波与模糊推理规则边缘检测算法相结合，提出了改进的模糊边缘检测算法；文献[5]通过主动轮廓最小化边缘检测方法，利用先验知识确定初始轮廓，结合参数主动轮廓模型与几何主动轮廓模型，提出了控制点搜索方法，采用控制点与样条形式检测边缘，扩展了捕获区域，降低了复杂度，但需要先验知识确定初始轮廓，对初始位置敏感，容易使能量函数的最小化过程收敛到局部极值点，甚至发散；文献[6]利用基于小波变换的多尺度边缘检测方法,在小波域中对图像分解的弱边缘进行适当加强，对低频系数采用模极大值法进行边缘处理，同时对边缘细节比较多的高频系数采用多尺度形态学算法进行边缘检测，最终得到较完整的图像边缘。

针对遥感图像多尺度地物特性，为了在快速检测遥感图像边缘的同时保持较高的精确度，本文提出了一种基于形态学多尺度自适应均衡的遥感图像边缘检测方法，在不明显增加方法复杂度的前提下，快速检测出完整清晰的遥感图像边缘。

1 方法流程

方法流程如图1所示。

2 多尺度自适应均衡边缘检测

2.1 多尺度结构元素模版

结构元素B作用于图像f，大尺度结构元素能够滤除微小边缘信息但容易造成漏检，而小尺度结构元素容易造成假边缘，同时单一方向结构元素只能提取单一的形态学特征，输出图像中只包含单一方向信息，造成边缘出现断裂。因此本文采用多尺度结构元素分别对图像进行形态学边缘检测，输出多幅包含不同边缘信息的图像，然后进行自适应均衡，检测结果包含不同尺度和方向的边缘信息使得边缘更加完整。本文采用尺度为1～4的圆形结构元素和0°,45°,90°,135°不同方向的尺度为3的线性结构元素。

2.2 形态学重构

本文采用形态学开重构运算，可以较准确地恢复腐蚀后的目标形状，相比经典开运算，可较好地保持目标轮廓边缘。若g是掩模，f是标记，则从f重构g可采用如下步骤：

1)将h1初始化为标记图像f；

2)选取多尺度圆形结构元素和四方向线性结构元素；

3)执行hk+1=(hk⊕B)∩g，直至hk+1=hk。

标记f必须为g的一个子集，即,f⊆g。

由图2可知，开重构运算可以有效滤除大于结构元素的明亮部分，同时不会改变图像中原有的目标结构，处理后图像边缘不会出现偏移，避免了目标畸变，同时滤除了噪声。

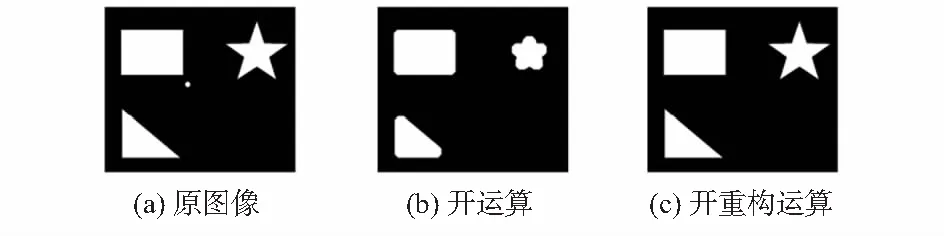
图2 开运算和开重构运算对比

2.3 膨胀型形态学梯度

对于纹理较为复杂细致的地物，增加纹理宽度容易使边缘模糊。为了得到精确边缘，本文采用膨胀型半梯度，即用膨胀后图像减去原灰度图像，提取到的边缘为单像素宽度，边缘相对清晰[7,8]。利用梯度提取地物边缘时，采用不同方向和尺度的结构元素进行边缘检测，不仅可以抑制噪声而且能够较好的增强边缘。假设g为梯度图像，则膨胀型形态学梯度可表示为g=(f⊕B)-f。

2.4 自适应均衡

在均衡过程中考虑不同尺度、不同方向结构元素的检测图像占有不同的比重[8]，利用统计图像灰度值方差进行均衡化。图像灰度值方差能够反映图像每个像素点的灰度值相对于该图像平均灰度的分散情况，图像的灰度值方差越大，说明灰度值的分布越分散，灰度层次越丰富，所含细节内容越多，包含的边缘信息越多。灰度值方差s2定义为

(1)

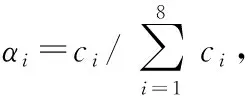
3 实验结果

为了验证本文方法对遥感图像边缘检测的效果和性能，在MATLAB 7.0环境下对大小为819×676的某城市遥感图像(图3(a))进行了边缘检测仿真，其中Prewitt算子检测，较多的边缘显示不完整，无法形成完整的边缘轮廓，细节部分较少；Log算子能够检测出大部分的边缘；Canny算子基本检测出了边缘轮廓，但存在假边缘；基于双边滤波的Canny算子检测到的假边缘较少，但边缘的完整性依然存在不足，桥梁存在明显断点；图3(f)～图3(b)为传统形态学边缘检测图像中,图3(f)因检测尺度单一，有较多细节边缘未被检测，另2种方法图3(g),图3(h)由于检测方向单一，图中边缘断点较多，无法形成完整清晰的边缘。

图3 边缘检测实验结果对比

本文方法增加尺度和方向上的边缘信息后，相比经典算子可以检测出更完整清晰的边缘，相比改进的Canny算子，在部分细小边缘上略显不足，但边缘较明亮突出。

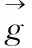
(2)

式中F(i,j)为图像的第i行，第j列的灰度值；M,N分别为图像的总行数和总列数,i为灰度级，pi为每一灰度级出现的概率。平均梯度越大则图像边缘越容易分辨。信息熵越大说明图像包含的信息越多。

从表1可知，本文方法在运算时间上略低于经典算子，明显低于采用双边滤波的Canny算子，表明算法复杂程度没有明显增加；平均梯度低于Canny算子，但也处于较高水平，说明检测到的边缘较为清晰完整；熵明显高于经典算子和改进的Canny算子，说明检测到的边缘包含更多的信息。本文方法在没有增加方法复杂度的情况下，明显提高了信息量，同时边缘也具有较高的清晰度和完整性。

表1 不同方法指标对比

为了验证本文方法的抑制噪声性能[9～11]，对大小为687×736的某城市遥感图像加入了0.1的椒盐噪声后(图4(a))进行边缘检测，检测结果如图4，并计算峰值信噪比(peak signal to noiseratio,PSNR)。其中Prewitt和Log的检测结果中出现较多由于噪声而引起的假边缘，图Canny和改进Canny算子假边缘较少，但边缘断点较多。图4(d)因单一尺度检测而使较多细节边缘缺失，图4(f)～图4(h)因检测方向单一只对横向、竖向等特定方向的检测效果较好，同时对噪声抑制能力较低，存在部分噪声引起的假边缘。本文方法抑制较多噪声干扰的同时，避免了假边缘的出现，同时本文检测方法的PSNR(8.544 5)略高于经典算子(8.258 7)和改进的Canny算子(8.368 7)，表明在一定程度上可以降低噪声干扰。

图4 加入椒盐噪声后检测结果对比

4 结束语

为完整快速地检测遥感图像边缘，提出一种基于多尺度自适应均衡的遥感图像边缘检测方法，在一定程度上改善了经典边缘检测算子处理图像时存在的不连续与不完整现象，同时具有一定的抑制噪声能力。