基于改进BBO算法的FCM图像分割方法*
2018-09-27胡晓辉王鸿闯
李 薇, 胡晓辉, 王鸿闯
(兰州交通大学 电子与信息工程学院,甘肃 兰州 730070)
0 引 言
生物地理学优化(biogeography-based optimization,BBO)算法是Simon D提出的一种新兴的智能优化算法[1,2]。由于其独特的迁移机制以及强大的信息共享能力,使得BBO算法得到了广泛的应用。如李静文等人[3]利用BBO算法对最优潮流问题进行优化;陈珍等人[4]将BBO算法应用到电力系统的经济调度问题。在标准的BBO算法中,迁移算子只选取了已存在个体的特征,使得信息的使用效率很低,导致收敛速度较慢。
模糊C均值(fuzzy C-means,FCM)算法是1974年由Dunn J C提出并由Bezdek加以推广的[5]。算法的关键是如何选取合适的初始值以获得最佳分割效果。但标准的模糊聚类是一种局部搜索算法,若初始值选取不当很容易陷入局部最优[6]。可通过引入智能算法对FCM的初值选取优化,如张红旗等人结合遗传算法和FCM进行草莓图像的分割研究[7]。
本文针对FCM算法进行图像分割时容易陷入局部最优的问题,引入BBO优化算法寻求全局最优聚类中心,并对算法的迁移和变异算子进行改进,提高算法效率,使算法能够快速收敛到全局最优解,提高寻求聚类中心的效率和准确性。
1 基本的生物地理学算法
在生物地理学优化算法中,每个个体称为一个栖息地,其中每个栖息地通过栖息地的适宜度指数(habitat suitability index,HSI)评判该栖息地的好坏。
生物地理学优化算法包括迁移和变异2个主要的操作。
迁入率λ和迁出率μ影响栖息地物种的迁移,与物种数量息息相关,设当前物种的迁入率λ和迁出率μ函数为λi和μi,则有
λi=I(1-Si/Smax),μi=E(Si/Smax)
(1)
式中I为最大迁入率,E为最大的迁出率,Si为当前种群数量,Smax为最大种群数量。
栖息地发生突然变异的概率与该栖息地的生物物种数量成反比,物种数量为i的栖息地发生变异的概率mi为
(2)
式中Ps为物种数量为S的概率,mmax为给定的最大变异概率。
2 改进的BBO算法
2.1 选择操作
本文增加选择算子,不仅加快了收敛速度,而且对于后续的迁移和变异有一定程度的帮助。算法1为选择算子的伪代码,NP为保留优秀解的个数,HSIj为旧解的适宜度指数,HSIx为新解的适宜度指数的值。
算法1选择算子
fori=1 toNP
ifHSIj(i) 用新解替换旧解 end if else 保留旧解 end for 标准的迁移操作是在已有的栖息地的物种之间进行迁移,对于全局的搜索能力较差,且对于标准BBO算法的迁移操作来说,某个迁出率较高的栖息地中的迁出对于迁入率较高的栖息地并不一定完全最优。 为了提高其的全局搜索能力并且使得迁移更加的有效,本文在BBO算法选择操作的基础上,利用保留的优秀解对迁移操作进行。其中优化公式为 Hi←He+R(-1,1)×(Hr-He) (3) 式中Hi为选定的进行迁入的栖息地,He为选定的进行迁出的栖息地,Hr为选择的优秀解,R(-1,1)为[-1,1]之间的随机数。迁移策略的伪代码如算法2,其中N为栖息地的数量,D为单个栖息地中的特征数量,rand(0,1)为(0,1)之间的随机数。 算法2改进的迁移算子 fori=1 toN forj=1 toD 根据迁入率λi选择待迁入的栖息地Hi if rand(0,1)<λi 选择需要改变的特征Hi(i,j) 根据迁出率μi选择需要迁出的栖息地He if rand(0,1)<μi end if end if end for end for 在BBO算法中,标准的变异操作使用随机生成的特征值代替选中栖息地原有的特征值,具有一定的盲目性,可能导致BBO的收敛速度变慢。为此,本文提出了一种通过优秀解与所选栖息地的特征值进行二进制计算从而得到较优的变异特征值的方法,对于变异产生的盲目性进行一定程度的降低,并且在收敛速度上有一定程度的提高。具体为 Hi←Hr1+Fi⊗(Hr2⊕Hr) (4) 式中 “⊕”为异或操作,“⊗”为与操作,Hr1和Hr2为随机产生的2个不同的特征值,Hr为使用选择操作保留的最优个体;Fi为二进制变异尺度因子,是随机产生的二进制位串。变异策略的伪代码如算法3所示。 算法3变异算子 fori=1 toN 选择出待变异的栖息地Hi 根据Pi计算出mi,然后用mi选择特征Hi(i,j) if rand(0,1) 由式(4)的特征值代替Hi(i,j) end if end for 本文将改进的BBO算法引入到FCM聚类中心的选取,提高聚类中心的准确性和后续的图像分割效率,为了验证本文提出方法的有效性,选取了2个典型图像(baboon和Lena)进行实验,同时进行基于遗传算法[8,9]以及标准BBO算法的FCM图像分割实验作为对比。 实验1分割baboon图像,设置C=3,结果如图1。 图1 baboon图像分割对比 实验2分割Lena图像,设置C=2,结果如图2。 图2 Lena图像分割对比 图像分割的结果通过划分熵和划分系数评价,划分系数Vpc,划分熵Vpe均是基于隶属度的聚类有效性函数指标,若Vpc的值越趋近于1,则聚类的程度越强。Vpe越趋近于0,聚类结构越明显,如表1所示。 表1 实验图像的有效性指标 从分割效果以及分割时间都可以看出,本文方法优于其他2种方法看,基于标准BBO算法的FCM图像分割法在迁移操作时有可能没有改变被迁入栖息地的适宜度指数,且在变异操作时缺少具体的变异方向。在基于遗传算法的FCM图像分割法中,遗传算法中的交叉操作无法根据适应值的不同情况来改变交叉基因的比例,更加重要的是交叉操作的片段来自同一个体,很容易导致陷入局部最优[10,11]。 基于以上分析可以得出结论,基于改进的BBO优化算法的FCM图像分割方法能快速有效地分割复杂图像。 本文提出了基于改进的BBO优化算法的FCM图像分割方法,目的在于降低图像分割的效率和改善分割效果。实验结果显示本文提出的分割方法行之有效。2.2 改进的迁移操作
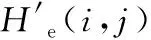
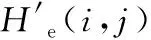
2.3 二进制变异操作
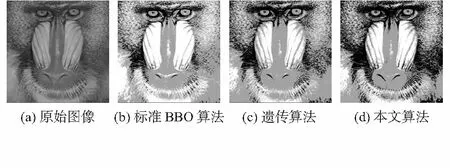
3 实验与结果分析


4 结 论
