基于红外辐射特性的海面温度研究∗

何伟怡 李向春 明德烈

（1.华中科技大学自动化学院 武汉 430074）（2.火箭军研究院 北京 100094）

1 引言

海面红外辐射特性与本身的物理特性和环境因素密切相关，其中海面在红外辐射特性分析下，涉及到的物理特性主要包括海面温度、海面发射率和反射率［1］。海面温度和发射率影响着自身红外辐射能量，海面反射率则影响其对外界太阳辐射和天空背景辐射的反射比例［2］，两者最终影响海面在红外波段下辐射到探测器的能量值，所以在对海面红外辐射特性的研究中，这三个参数就显得至关重要。本文主要介绍海面温度模型的建立和求解。

海面海水温度与测量点所处经纬度、季节天气均有紧密联系，因而具有多变性。目前，根据不同的要求，测量海水温度主要有下面几种方法［3］：一是使用投入式测温仪进行测量，这种方法主要适用于对特定海域固定深度的多年温度变化检测；二是采用遥感技术对海水温度进行测量，此方法主要用于对大面积海域或者全球海域温度的检测。目前，包括中国在内的许多国家已经发射了多颗极轨气象卫星，为全球海域全方位、多角度观测提供了便利。

然而，由于海洋极端天气条件对船只及人员安全性的威胁，以及特定海域局势军事敏感性的限制，使用投入式测温仪对特定海域进行海水温度的测量就受到较大的限制。基于遥感技术的海温测量对于反应海水表层24小时内的温度变化精确度以及时效性有待考量。所以，前述测量方法适用于气象学研究，但无法为红外实时仿真所使用。

针对海面红外仿真实时性高、对海水表层温度变化精度要求高的特点，需要建立专门的模型计算海水表皮在一天之中随时间推移的变化，其中一种常用的方法是查阅当地海域的实测资料（海面温度、大气温度、相对湿度和风速等参数），然后对实测数据进行分析，研究水温、气温以及其它气象参数之间的数学关系，推导包含以上参数的回归方程和回归曲线，得到一个计算海面温度的经验公式［4］。这种方法的优点在于计算方便，能满足一些实时性要求较高的系统需求，但是缺点也很明显，因为经验公式是通过当地实测数据的分析推导而来，存在一定的误差，并且公式的局限性较大，如果要计算另一片海域的海面温度，就需要重新分析实测数据和推导回归方程。

计算海面温度的另一种方法就是对海面温度进行数学建模，即利用热平衡理论对海面建立热平衡方程，把海面温度当作热平衡方程的未知量，通过求解平衡方程中其它分项的值，最后再计算得到海面温度。

本文将采用热平衡方程来计算海面温度，并针对海面热平衡方程中的海面热传导分量的计算方法进行研究。在求解方程过程中，首先通过隐式差分方法对方程进行空间和时间维度上离散化，接着将方程转换成矩阵运算形式，最后利用追赶法求解海面温度。

2 海面温度场景模型建立

根据能量守恒定律，对于整个海水表面薄层来说，任意时刻，表面从外界吸收的能量与表面向外界散失的能量满足以下热平衡方程［5］：

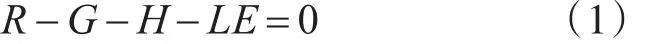
其中各项含义如下：

R为净入射辐射通量，即表面从外界（太阳、天空等）获取的净辐射通量，方向为从上向下指向表面为正。不考虑外部热源的情况下，其值等于太阳入射通量和天空入射通量与表面自发辐射散失的辐射通量之差：

G为海面向下热传导热量，即地面表面朝下向更深层热传导散失的热量，方向为从表面向下为正；

H为海面与大气交换热量，即表面与大气发生热交换散失的能量，方向为从表面向上为正；

LE为海面蒸发热量，即表面由于水分蒸发作用而散失的热量，方向为从表面向上为正。

除了G分量，方程剩余分量与传统方法中的热平衡方程一致。传统方法计算得到的G分量表达式较为简单，不能正确反应出海水表面向下传导的热量，得到的结果误差较大。

本文采用一维傅里叶热传导方程来计算海面向下传导的热量，求解方程过程中，对方程进行空间和时间维度上进行离散化，通过设定初始值迭代计算得到逐小时海面温度。得到海面温度结果较传统方法更准确，因此计算复杂度也较大，可以通过离线计算和查表方式来解决实时性问题。

接下来具体介绍热平衡方程中每个分项的具体计算方式。

1）净入射辐射热量

净入射辐射通量包括太阳入射热量、天空入射热量和海面自发辐射热量，其中太阳辐射［6］为短波辐射，到达地球大气层外的太阳辐射可以通过日地距离修正太阳常数精确计算得到；天空辐射［7］分为大气辐射和云层辐射，均为长波辐射；物体通过辐射向外散发能量，由于地面物体的温度不高，自发辐射也主要是长波辐射［7］。以上三种辐射能量的计算比较常用，这里就不详细展开。

2）海面与大气交换热量

海面与大气之间交换的热量也称感热通量，热量交换的速度和方向与表面与近地层空气的温差以及风速等因素相关。通常采用空气动力学公式进行计算［8］：

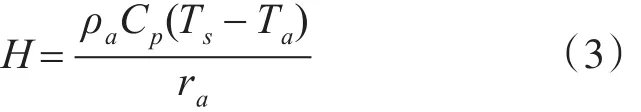
其中，ρa为湿空气的密度，Cp为空气的定压比热容，Ts为表面温度，Ta为大气温度，ra空气动力学阻力［9］。

3）海面蒸发热量

海面蒸发热量又称为潜热通量，与感热通量不同，该通量为表面水分蒸发作用带走的热量，对于海面水分可以采用以下公式［8］：

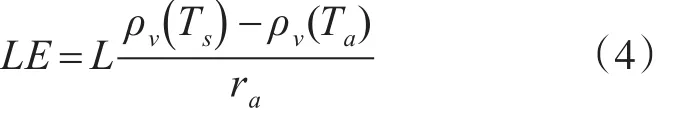
其中，L为水的汽化潜热，ρv为绝对湿度。

4）海面向下热传导热量

海面向下热传导热量的计算满足傅里叶方程，对于海面薄层，按一维热传导计算，方程为［10］

其中，T为表面层温度，λ为材质的导热系数。特别地，表面层传导的热量G为

2.1 海面温度场模型分析

由于在研究海面温度计算中，我们忽略洋流、内部漩涡和表面温度差异等因素，认为海面在某一时刻具有相同的温度，并且在一定深度海水温度是保持一个定值［11］，那么可以把研究对象缩小成具有一定深度的海水薄层，海洋表面满足上方给出的表面热平衡方程，海水薄层底部再往深处的海水则保持一个恒定的温度，薄层内部则满足一维傅里叶热传导方程，只存在层与层之间的热量传递。

经过上述对海面模型的简化和分析，将海水薄层沿着垂直方向上进行空间划分，从海面到薄层底部分成若干层，Zi为每一层的厚度，如果不考虑层与层之间温度变化速度的差异，可以把每层厚度设成相同的值，本文采用等比数列设置薄层厚度，越往深处薄层厚度越大。

除了进行空间划分，还需要对海水薄层进行时间上的划分，由于红外仿真系统是模拟海面一天24小时的辐射变化，所以时间维度上从0到24小时划分，步长的△t设成定值。

2.2 海水薄层内部温度场

对于薄层内部，由于我们忽略了洋流等复杂因素的影响，海水只存在层与层之间的能量传递，即满足一维傅里叶热传导方程，那么将热传导方程从空间和时间维度上进行离散划分，转为隐式差分方程［12］：

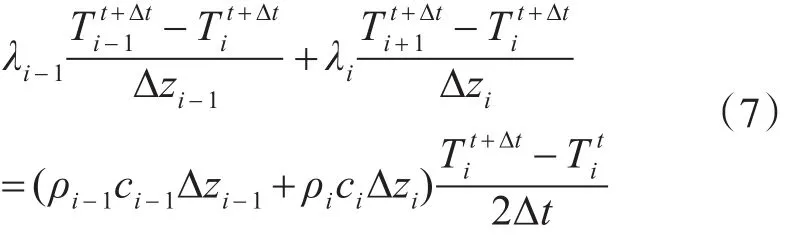
其中λi为每一层的导热系数，由于忽略复杂因素的影响，每层海水的导热系数相同；△Zi表示第i层的厚度，Tit表示在t时刻下的第i层海水的温度；ρi表示第i层海水的密度；ci表示第i层海水的比热容；这里每层的密度和比热容都是相同值。

在公式中t时刻下每层温度值和每一层厚度、海水导热系数、密度、比热容都是已知的，需要推导t+Δt下每一层的温度，那么将上述差分公式变换成如下形式：

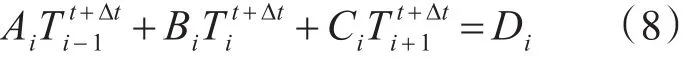
其中经过公式换算，得到A、B、C、D系数表达式如下所示，其中i大于1，且小于n：经过上述公式转换，可以很方便地将方程式转换成矩阵运算，如下所示：

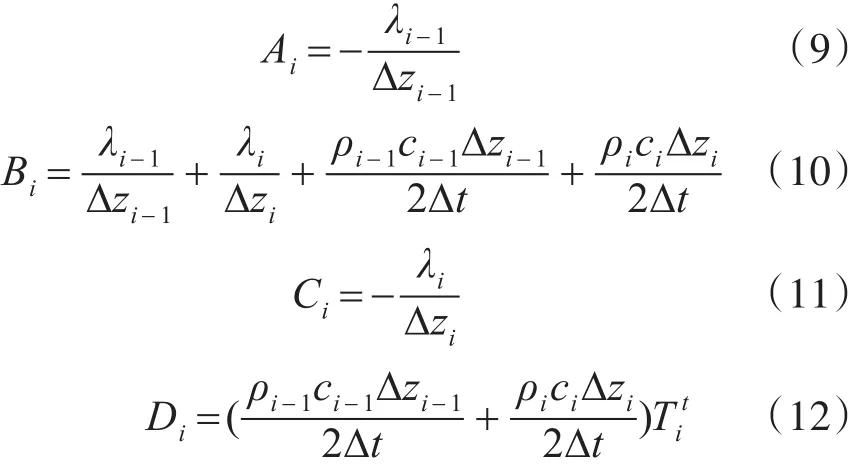
由于这里讨论的是海水薄层内部的能量交换，所以上述矩阵运算中，从第二层到第n-1层的系数是已知的，第一层和最后一层的A、B、C、D系数仍是未知量，还需要对上下边界进行单独推导分析。

2.3 海水薄层上边界温度场

海水表面不但要和第二层海水进行热量交换，还和大气直接接触，涉及到大气背景辐射、风速和相对湿度等因素的影响，所以一维傅里叶热传导方程不适合用于计算表面温度。这里需要结合之前提到的表面热平衡方程来解算表面温度场数据，同样采用隐式差分的方式，对该方程进行空间和时间维度上离散化，得到如下公式：

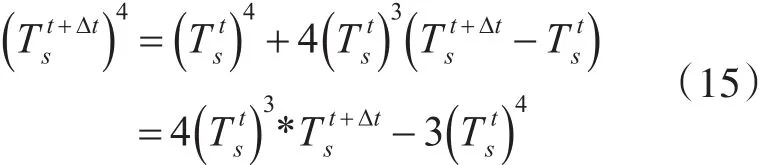
将一阶微分近似后公式代入表面热平衡方程中，得到如下公式：

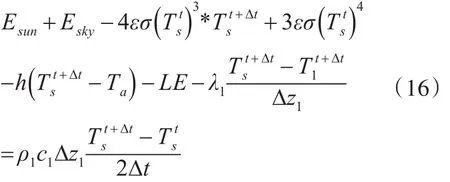
和上小节类似，转换成如下形式：

其中经过公式换算，得到A、B、C、D系数如下所示：

通过对表面热平衡方程进行隐式差分转换，得到矩阵运算中系数A、B、C、D的表达式。值得一提是这里系数A值为0，这是由于海面不存在上一层海水，无需与上层海水交换热量，所以不需要上层海水温度的分量。

2.4 海水薄层下边界温度场

对于海水薄层下边界而言，除了要和倒数第二层海水进行热量交换，它还要和薄层底部以下的海水进行热量交换；这个区别在于，我们把薄层底部以下海水经过复杂的热量交换，达到稳定的温度值，而这部分辐射热量计算较为复杂，需要单独处理。这里采用方式是将底部能量交换总结为一个换热系数αin，从而底部热传导方程如下所示［12］：

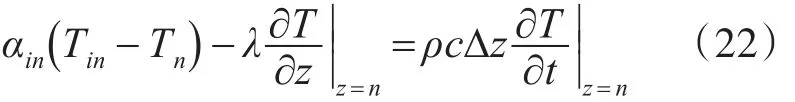
其中，αin为换热系数；Tin为海水薄层底部以下海水的温度值，采用经验数据；Tn为海水薄层底部的温度值。

同样由于该热传导方程存在微分项，需要对其进行空间和时间维度上离散化，经过隐式差分转换得到如下公式：

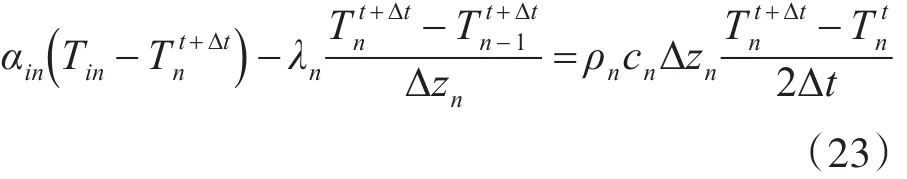
和上小节类似，转换成如下形式：

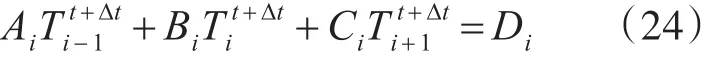
其中经过公式换算，得到A、B、C、D系数如下所示：

2.5 海水薄层温度场计算过程

通过对海水薄层上下边界和内部热量传递方程的解算，最终将热传导方程转成矩阵运算，公式中系数矩阵和等号右边的列向量为已知量，公式中第二项的列向量表示为下一Δt时刻每层海水的温度值，为待求解。通过分析公式中第一项系数矩阵为三对角矩阵，其非零元素集中分布在主对角线和其相邻两个次对角线上，我们把这种矩阵公式称为三对角方程组，可以通过追赶法来进行求解［13］。

在利用追赶法求解该三对角方程组过程中，由于方程式从空间和时间维度上进行离散化，意味着温度场数据的求解是一个递推的过程，需要拟定一个初始值才能解算出下一Δt时刻的海水薄层每层的温度值。本文拟定以下起始条件：时间起点为凌晨4点，此时海面层温度与大气温度相同，海水表层以下每层温度按线性插值计算得到。设定该起始条件基于以下假设：经过整个夜晚的降温和热交换，海水表面的温度应与大气温度相近。

求解过程如图1所示，图1左侧为初始温度场数据的设置，选定的时间为凌晨四点，海水表面温度与大气温度相等，然后通过线性插值得到表层以下每层海水的温度值，接着根据初始值按步长Δt进行迭代，直到解算出仿真时刻的海水表面温度。

3 实验结果分析

首先本文先进行海面温度与大气温度比较分析。由于海水表面直接接触着大气，大气温度直接影响着海水温度，使得大气温度和海水温度有着相同的上升下降趋势；接着将海面温度仿真数据和实际测量数据进行对比验证，但是由于海面温度逐小时数据难以获取，比如中国气象网中需要较高权限才能下载全球海平面温度资料数据，普通学生用户无法得到，只能从国家海洋环境预报中心网站中获取邻近海域的最低最高温度数据，所以本文将用仿真计算得到的海面温度数据与同一海域的最高最低温度数据进行比较，观察仿真数据是否分布在最高最低温度的范围附近。

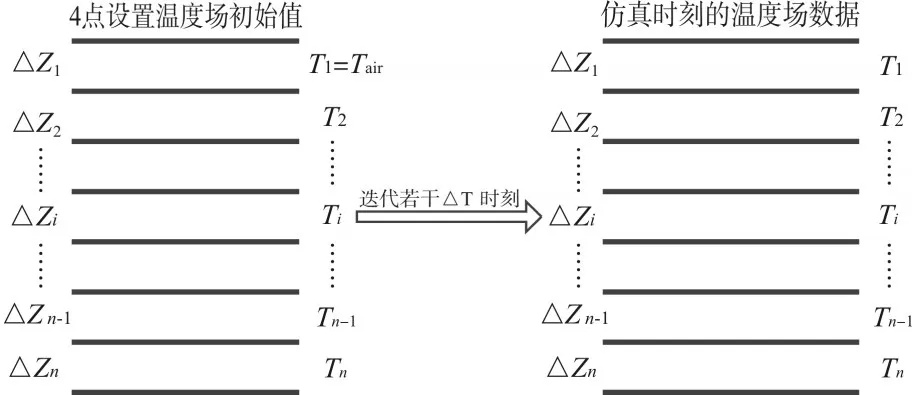
图1 迭代计算海面温度

本文采用网上气象数据和海洋温度数据的时间为2016年8月和2016年1月，分别代表着夏天和冬天季节，海域经纬度位置约为东经118.1°，北纬38.7°。其中海面温度计算过程中所使用到的参数信息如表1所示。

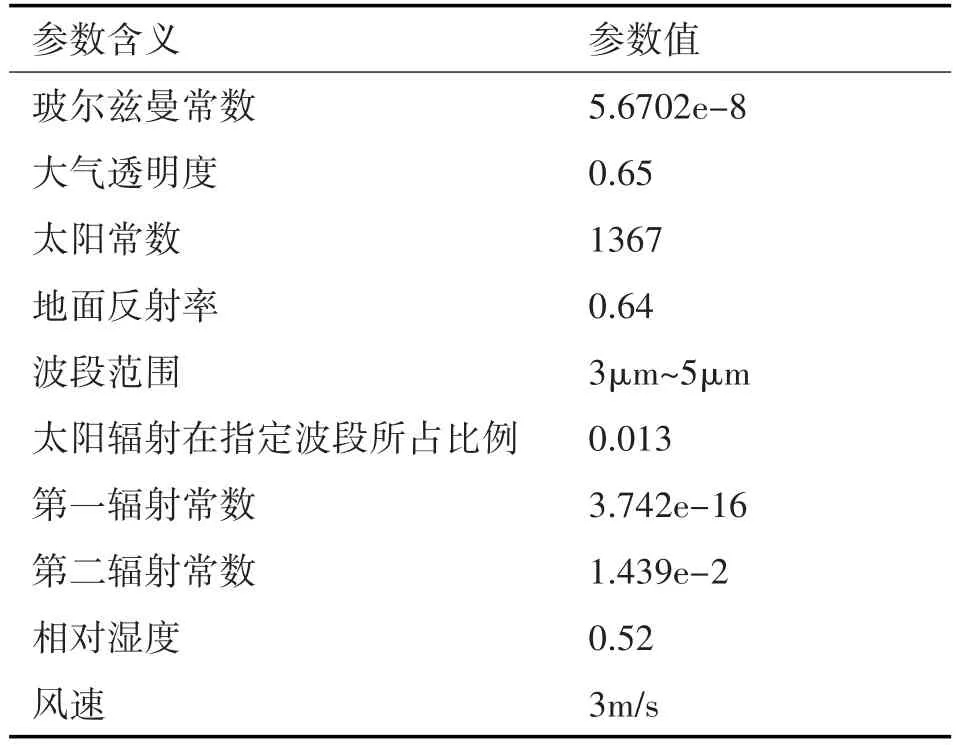
表1 参数信息

图2 夏天海温和气温比较

以上两幅图分别为夏天和冬天季节下海面温度仿真数据和气象网大气温度数据的对比图，从图中可以看出，凌晨时段海水温度比大气温度高，海水温度变化比较缓慢，然后从日出时段后，由于大气的比热容较小，升温速度较海面快，大概下午14点到15点大气温度达到了峰值，随后海面温度也跟着达到峰值，最后随着日落两者的温度也逐渐降低。因此可以看出，海面温度仿真数据和实测大气温度具有大致相同的上升和下降趋势，说明本文海面温度计算模型能较好反映大气温度和太阳辐射对海面温度的影响。

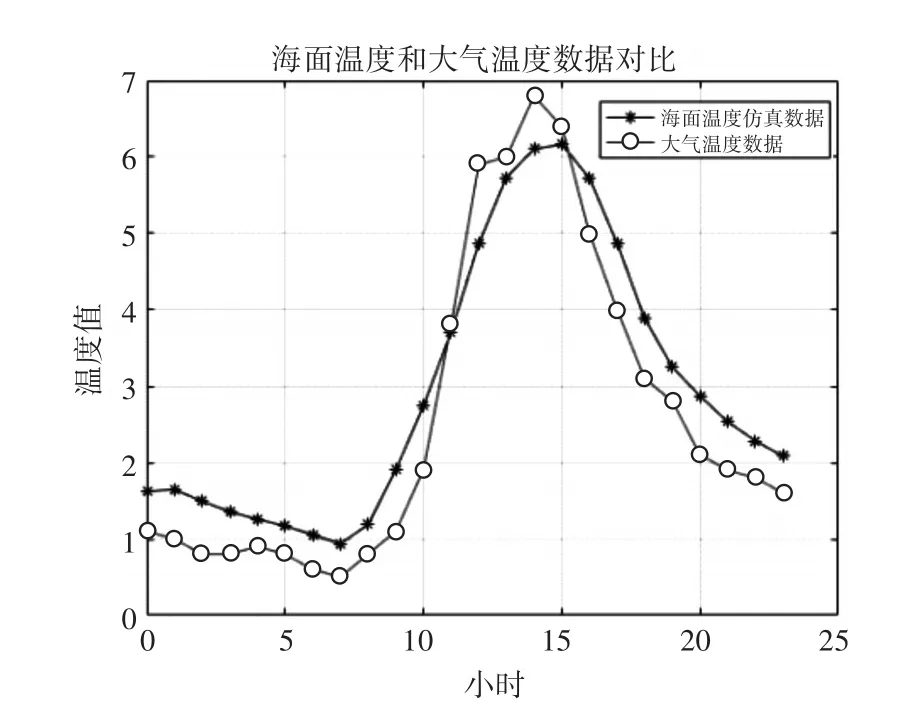
图3 冬天海温和气温比较

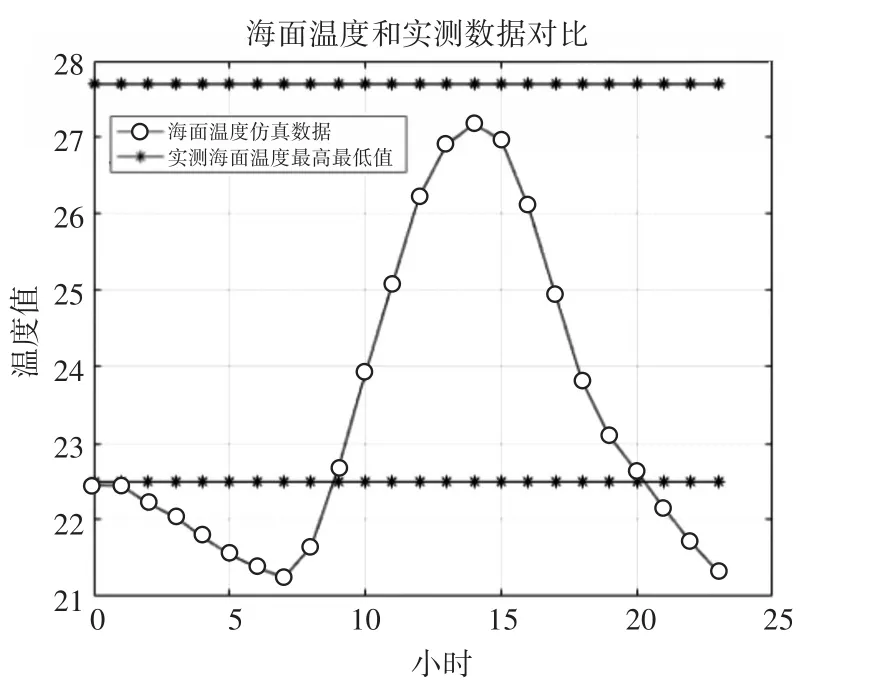
图4 夏天温度数据对比

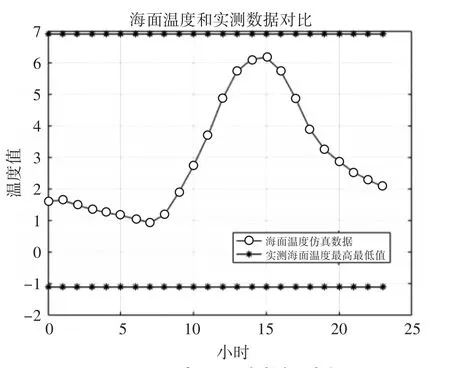
图5 冬天温度数据对比

从上面两幅图可以看出，虽然海面温度仿真数据与实测海面温度范围有一定的误差，这是因为本文忽略了洋流等复杂因素的影响，在整体上本文的仿真数据还是能很好地分布在最高最低值附近，较好反映实测海面温度变化的范围，从而表明本文海面温度计算模型具有较好的正确性。

4 结语

本文从海面的热平衡方程出发，介绍了平衡方程中的各项：太阳辐射、天空的长波辐射、海水的蒸发潜热、海水对大气的热传导和海水向深处的热传导分量，在建立海面热平衡方程基础上，利用隐式差分方法将海面模型在空间和时间维度上进行离散化，接着将方程转换成矩阵运算形式，最后利用追赶法迭代求出仿真时刻的海面温度数据。并对海面温度的仿真数据进行对比验证，分别和历史大气温度数据、海面最高最低温度数据进行比较，实验结果表明仿真数据满足实际温度变化趋势，说明本文海面温度计算模型具有较好实用性，能为海面背景红外辐射模型提供相关输入，同时可以为海洋环境的红外检测提供参考。