Robust extended Kalman filter with input estimation for maneuver tracking

Yuzi JIANG,Hexi BAOYIN

School of Aerospace Engineering,Tsinghua University,Beijing 100084,China

KEYWORDS Extended Kalman filters;Input estimation;Maneuver detection;Maneuver tracking;Orbit determination

Abstract This study investigates the problem of tracking a satellite performing unknown continuous maneuvers.A new method is proposed for estimating both the state and maneuver acceleration of the satellite.The estimation of the maneuver acceleration is obtained by the combination of an unbiased minimum-variance input and state estimation method and a low-pass filter.Then a threshold-based maneuver detection approach is developed to determinate the start and end time of the unknown maneuvers.During the maneuvering period,the estimation error of the maneuver acceleration is modeled as the sum of a fluctuation error and a sudden change error.A robust extended Kalman filter is developed for dealing with the acceleration estimate error and providing state estimation.Simulation results show that,compared with the Unbiased Minimum-variance Input and State Estimation(UMISE)method,the proposed method has the same position estimation accuracy,and the velocity estimation error is reduced by about 5 times during the maneuver period.Besides,the acceleration detection and estimation accuracy of the proposed method is much higher than that of the UMISE method.

1.Introduction

The problem of tracking a maneuvering satellite has received attentions in recent years.1–4In general,Kalman Filter(KF)has been used successfully to determine and predict the orbit of a satellite.However,when the target is non-cooperative,which means there is no priori information on the maneuver,the tracking performance of KF method degrades or even diverges.5

Certain methods have been formulated to solve this problem.Some methods solve the problem by tolerating the model mismatch in the tracking process.Maneuver reconstruction is a post-process method for determining the period,the magnitude and the direction of a maneuver by fitting two separated arcs that bound the maneuver–the pre-maneuver and postmaneuver trajectories.6This method performs better than KF.However,the post-process method cannot meet the requirement of the real-time maneuver tracking.The reinitiation of orbit determination is another kind of feasible method to converge the estimation after the occurrence of a maneuver.Usually,the maneuver is detected as a fault or an abnormal event of the dynamics system by a fault detector or indicator.When the maneuver is detected,the filter is reinitiated with a huge enough covariance.Then the postmaneuver orbit is determined as a new initial orbit,and the model mismatch caused by the maneuver is treated as an initial state error,which is readily accommodated by ordinary orbit determination methods.Patera7proposed a data processing method for detecting space events including satellite maneuvers.However,a catalog of the tracked satellite is required.Jwo and Lai8,and Wang et al.9used a fading factor to detect the maneuver and re-initiate the covariance of the state estimation,which is based on the Strong Tracking Filter(STF)method.10Those methods provide accurate state estimations when the predicted state covariance is scaled properly by the fading factor.The main disadvantage of these methods is that they only provide the estimation of the state but not the estimation of the maneuver.

Other methods solve the problem by eliminating the mismatch caused by maneuvers.The augmented state space method is one example.In this method,the unknown maneuver acceleration is augmented to the state space and estimated with the state together.Therefore,a dynamics model of the maneuver acceleration is needed.Kumar and Zhou11proposed a current statistical model for the maneuver acceleration,and developed an adaptive algorithm for tracking a maneuvering target.Whang et al.12assumed that the maneuver model was a first-order Markov process,and the maneuver onset time was detected by the pseudo-residuals.Lee and Tahk13assumed that the maneuver occurred only once inside the detection window and the maneuver acceleration was constant during a maneuvering period.Li and Jilkov14summarized a lot of kinds of maneuver dynamic models in their works.Khaloozadeh and Karsaz15assumed that the unknown acceleration was constant in the navigation model.Ko and Scheeres16,17used the thrust-Fourier-coefficient event representation method for detecting and estimating the maneuver acceleration,and the thrust-Fourier-coefficients were considered as constant in the navigation model.In order to obtain the dynamic model of maneuvers,these methods usually make some assumptions about unknown maneuvers.Therefore,when an actual maneuver deviates from the assumptions,the tracking performance of these methods degrades,which limits their application.

Another kind of method is the Input Estimation(IE)method.In this kind of method,a maneuver is considered as an unknown in putin the dynamics system,which is distinguished from the state.Kitanidis18proposed an optimal recursive state filter in the presence of unknown or highly non-Gaussian system inputs.The stability and convergence conditions of this method were proposed by Darouach and Zasadzinski19.However,Kitanidis’s work did not provide the estimation of the unknown input.Hsieh20proposed a robust two-stage Kalman filter for estimating both the state and the unknown input.Darouach et al.21proposed a recursive state filter with unknown input,but the unknown input needs to be included in outputs.Gillins and De Moor22,23proposed an unbiased minimum-variance input and state estimation method both in the system with direct feedback and without direct feedback.Cheng et al.24proposed an unbiased minimum-variance state filter with unknown input,which has a milder requirement on the distribution matrix than the previous work.19Ding and Fang25proposed an adaptive modified input and state estimation method,which provides a better maneuver estimation compared with Gillins and De Moor’s method.22

However,when the problem of tracking a non-cooperative maneuvering satellite is considered,the application of the IE methods may have some limitations.Usually,the maneuver acceleration estimate error of the IE method is quite large under the condition of the ground measurement accuracy,which influences the maneuver tracking performance significantly. Therefore,a Robust Extended Kalman Filter with Input Estimation(RIEEKF)method is proposed in this paper to overcome this shortage.First,an Unbiased Minimum-variance Input and State Estimation(UMISE)method is introduced to provide a rough maneuver acceleration estimate.Then,a low-pass filter is used to reduce the acceleration estimate error according to a proper analysis in the frequency domain.A threshold-based maneuver detection approach is developed to determine the start and end time of the unknown maneuver.Finally,a robust extended Kalman filter is presented for estimating the state of the maneuvering target.

The remainder of this paper is organized as follows.Section 2 introduces the orbital dynamics and the measurement model.Section 3.1 proposes the acceleration estimate method and the maneuver detection method.Section 3.2 proposes the robust extended Kalman filter for the state estimation.Section 4 presents simulations to demonstrate the feasibility of the method in various maneuver situations.A comparison between the proposed method and the UMISE method is given to demonstrate the performance of the proposed method.In the last section,conclusions and a discussion of the proposed method are presented.

2.Dynamics and measurement model

The orbit dynamics used in this paper can be expressed as

Adequate measurements are required for tracking the satellite.Measurements of range and range-rate from ground radar stations are employed in this paper.The measurements are modeled as

where r and Riare the position vectors of the satellite and the ith radar station,respectively;˙r and˙riare the velocity vectors of the satellite and the ith ground station,respectively;yρiand yviare the range and range-rate measurements from the ith radar station,respectively; ωρiand ωviare the measurement noises,which are assumed to be zero-mean Gaussian white noises.

The following linear discrete-time system can be obtained from Eqs.(1)and(2):

where xk∈Rnis the state of the satellite at the discrete time tk;Φk，k-1= Φ(tk，tk-1)is the state transition matrix from time tk-1to tk,which is derived asyk∈is the measurement data;Hkis the measurement mapping matrix,which is derived asis the maneuver acceleration at the discrete time step tk-1.The coefficient matrix Gk-1is defined using Eq.(1)as follows:

The measurement sampling interval is set as 1 s,and the standard deviations of the measurement errors are set as

3.Tracking maneuvering satellite with RIEEKF method

3.1.Unbiased minimum-variance input estimation with low-pass filter for maneuver estimation

Gillijns and De Moor22proposed an Unbiased Minimumvariance Input and State Estimation(UMISE)for a linear discrete-time system described in Eqs.(3)and(4).The basic framework of this estimation method is presented as follows:

It can be observed in Fig.1 that the maximum value of the acceleration estimate of the UMISE method is about 2 m/s2while the actual maneuver acceleration is just 0.1 m/s2during the maneuver period,which means that the actual maneuver is totally covered by the large acceleration estimate error.Because of this significant maneuver estimation error,it is difficult to distinguish the actual maneuver acceleration from the result of the UMISE method.Thus,when the measurement condition is same as what we assumed in Section 2,the UMISE method cannot provide a detection of the unknown continuous maneuver,and cannot provide a maneuver estimation with a satisfactory accuracy,which limits the tracking performance of the UMISE method.To overcome this shortage,a more accurate acceleration estimate method is proposed in this paper.

Fig.1 Comparison between actual acceleration and estimation of UMISE method.

Fig.2 UMISE acceleration estimate and actual maneuver acceleration in frequency domain.

Table 1 Parameters of multiple low-pass filters with different assumed maneuver acceleration.

Since the acceleration estimate of UMISE method has a large error which is difficult to be eliminated in the time domain,viewing this problem in the frequency domain may provide some new solutions.Fig.2 shows the results of the actual acceleration and the acceleration estimate of the UMISE method after a Fast Fourier Transform(FFT).As shown in Fig.2(a),the UMISE acceleration estimate is concentrated in the high-frequency part,while the actual acceleration is concentrated in the low-frequency part.However,the magnitudes of the UMISE acceleration estimate and the actual acceleration are close in the extremely-low-frequency part as shown in Fig.2(b).It indicates a way to obtain a more accurate acceleration estimate by filtering the high-frequency noise from the result of the UMISE method.In this paper,an adaptive Butterworth low-pass filter is used for the noise filtering.

To obtain an accurate maneuver acceleration estimate through the low-pass filter,a set of proper filter parameters is needed to be determined.The analysis of the UMISE acceleration estimate and the actual acceleration in the frequency domain can provide an approach to select the parameters of the low-pass filter.As shown in Fig.2(b),when the actual maneuver acceleration is 0.1 m/s2,the UMISE acceleration estimate and the actual acceleration are very close when the frequency is lower than fp=0.01 Hz,and the difference between them increases rapidly when the frequency is higher than fs=0.02 Hz.Thus,the normalized passband corner frequency Wpof the low-pass filter can be determined as Wp=0.02,and the normalized stopband corner frequency Wscan be determined as Ws==0.03.It should be noted that the ‘actual acceleration’we mentioned and illustrated in Figs.1 and 2 is just an assumed value in a priori simulation for determining the parameters of the low-pass filter,and the maneuver acceleration is unknown in the real tracking process.Thus,in order to adapt to the different maneuver situations,multiple sets of low-pass filter parameters are selected based on the different assumed maneuver acceleration,as shown in Table 1,and their performance will be demonstrated in the follow-up simulations.It will be shown that even if the parameters of the low-pass filters are determined by different assumed maneuver accelerations,they can still provide good results under different maneuver conditions.

3.2.Robust extended Kalman filter for state estimation

Fig.3 shows the acceleration estimate result after the low-pass filtering.It can be observed that the low-pass filtering method provides a more accurate acceleration estimate than the UMISE method(with the comparison between Fig.1 and Fig.3).However,there is still an estimation error of the maneuver acceleration,which may cause the degradation of the tracking performance both in the maneuvering period and the non-maneuvering period.In order to improve the tracking performance of the proposed method,the influence of the acceleration estimate error needs to be eliminated.

Fig.3 Result of acceleration estimate after low-pass filtering.

As shown in Fig.3,the acceleration estimate error can be divided into two parts.The first part is the fluctuation error,which exists in both maneuvering and non-maneuvering process.The second part is the sudden change of the error,which occurs at the beginning and the end of the maneuvering period.This part of the error is caused by the delay of the low-pass filter,and its magnitude is related to the magnitude of the maneuver acceleration.Therefore,this part of the error is difficult to be modeled in advance,because the maneuver acceleration is unknown in the real tracking process.These two parts of the acceleration estimate error will be discussed separately as follows to obtain better tracking performance.

First,the fluctuation error is considered.For convenience,represents the acceleration estimate after the low-pass filtering at epoch k-1.The actual maneuver acceleration dk-1can be presented as

where Δdk-1is the acceleration estimate error after the lowpass filtering.When only the fluctuation error is considered,Δdk-1shows a similarity to a random error or a vibration of the error.In order to obtain the statistical characteristics of this part of the error,the low-pass filtering method is applied in a non-maneuver situation.The result of the acceleration estimate in this situation is presented in Fig.4.

Monte-Carlo simulations are used to obtain more accurate statistical characteristics of the fluctuation error under different parameters of the low-pass filters.Table 2 shows the results of 100 Monte-Carlo runs.

The average value is quite small compared to the standard deviation as shown in Table 2.It means that the fluctuation of the acceleration estimate error can be considered as a zeromean random noise.In order to improve the tracking performance of the maneuvering target,the detection of the maneuver is necessary.It is difficult to detect the start time and the end time of the maneuver in the UMISE method because of the huge error of the acceleration estimate,as shown in Fig.1.However,the acceleration estimate after the low-pass filtering is much more accurate than the result of UMISE method and provides a possibility of maneuver detection.The maximum acceleration estimate error in non-maneuver periods has been obtained by the Monte-Carlo simulations,which means that the value of the acceleration estimate does not exceed this maximum value in non-maneuver periods.In other words,when the acceleration estimate exceeds the maximum value,it indicates that an unknown maneuver has occurred.In this way,a threshold-based maneuver detection method is proposed:

Fig.4 Acceleration estimate error after low-pass filtering in a non-maneuver situation.

where λdis the proposed threshold of the maneuver detection,and dxmax,dymaxand dzmaxrepresent the maximum acceleration estimate errors in three axes as shown in Table 2.When the absolute value of the acceleration estimate ‖‖ ＜ λd,the maneuver is considered not taking place at epoch k-1.On the contrary,when ‖‖ ≥ λd,it is considered that the maneuver has occurred at epoch k-1.When the maneuver is considered not happening,the value of the actual maneuver acceleration is zero:

Substituting Eq.(12)into Eq.(1)yields

In this case,the dynamics system does not have unknown inputs,and thus the classical extended Kalman filter can provide a good enough state estimation result.

where vd，k-1is the random noise with a variance as follows:

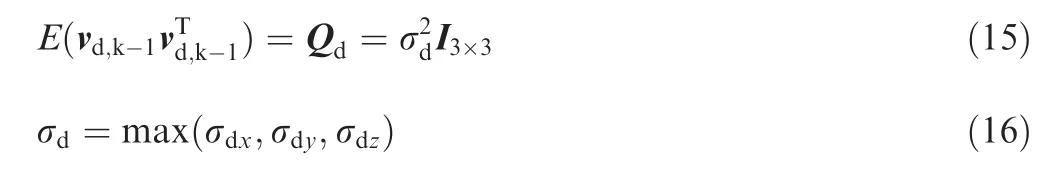
where σdx，σdy，σdzrepresent the standard deviations of acceleration estimate error in three axes,which are obtained in Monte-Carlo simulations,as shown in Table 2.Substituting Eq.(16)into(4)yields

Thus,the problem is transformed into a state estimation problem of a dynamics system with a known input^d*k-1and a process noise vd，k-1,which can also be accommodated by the extended Kalman filter method.

Combining these two cases,an adaptive extended Kalman filter is proposed to provide the accurate state estimation during both the non-maneuvering period and the maneuvering period.A maneuver indicator is defined as follows:

where χk-1=0 means that the target is not maneuvering at epoch k-1,and χk-1=1 means that the target is maneuvering.The state estimation and the covariance at epoch k are derived as follows:

Table 2 Statistical results of acceleration estimate error during non-maneuver periods in Monte-Carlo simulations.

When the maneuver indicator χk-1=0,this method of state estimation degenerates into an extended Kalman filter without unknown input.And when the maneuver indicator χk-1=1,the method transforms into an extended Kalman filter with a known input and a random process noise.

Next,the sudden change of the acceleration estimate error is considered.As described earlier,this part of the estimation error is difficult to model,and it can hardly be eliminated because of the delay of the acceleration estimate caused by the low-pass filter.When the maneuver starts or ends,the acceleration estimate error increases rapidly and it takes some time to converge,as shown in Fig.3.During this period,neither the non-maneuver model proposed in Eq.(12)nor the maneuver model proposed in Eq.(14)can match the actual maneuver acceleration.Thus,the result of state estimation deviates from the actual value,while the state covariance matrix cannot reflect this deviation during this period.The mismatch between the state estimation error and the state covariance leads to poor tracking performance.Therefore,an approach of scaling the state covariance is developed to tolerate the mismatch of the covariance,which is based on the Strong Tracking Filter(STF)method.6The scaled covariance is derived as follows:

where 0＜λ≤1 is the forgetting factor and it is selected as λ=0.95.β≥1 is the softening factor and it is selected as β =10.The scaling coefficient α*krepresents the comparison between the actual residual and the nominal covariance.When the actual residual is smaller than the nominal covariance,the coefficient α*kis equal to 1 and the state covariance remains unchanged.However,when the actual residual is larger than the nominal covariance,the value of the coefficient α*kis larger than 1,which means that the state estimation error is increasing and indicates the occurrence of an unknown maneuver.Then the prediction of the state covariance is scaled by α*k.With the scaling of the state covariance,the state estimation error caused by the sudden change of the acceleration estimate error is tolerated,and the state estimation can keep convergent.Therefore,the scaling of the covariance matrix enhances the robustness of the proposed method against the sudden change of the acceleration estimate error,and provides better tracking performance at the beginning and the end of the maneuvering period.

4.Simulations

To demonstrate the performance of the proposed method,several simulations are presented in this section.In these simulations,the initial position and velocity of the target are[-5726.21,-3472.06,1156.51]km and[-1.6,0.15,-7.49]km/s,respectively.The initial state estimation errors are[1,1,1]km for the position and[1,1,1]m/s for the velocity.In order to demonstrate the effect of low-pass filter parameters on the maneuver detection and tracking,three sets of filters with different parameters are used in the simulations.The parameters and the statistical characteristics of them are shown in Tables 1 and 2.The results of the proposed method are compared with those of the UMISE method proposed by Gillins and De Moor22.

Fig.5 Tracking performance in Case 1.

Fig.6 Tracking performance in Case 2.

In Case 1,the tracking process lasts 1000 s,and the maneuver occurs from 400 s to 600 s.The magnitude of the maneuver acceleration is 0.5 m/s2and the maneuver is in the direction of satellite’s velocity vector.Fig.5 shows the results of the proposed method in Case 1.The acceleration estimate of the low-pass filter 1 is not zero at 407 s after the beginning of the maneuvering period and returns to zero value at 615 s after the end of maneuver process,which means that the maneuver detection delay is 7 s and 15 s,respectively.The maneuver detection delay of the low-pass filter 2 is 6 s and 90 s,and the delay of the low-pass filter 3 is 2 s and 340 s,as shown in Fig.5(a).It can be observed that filter 3 has a smaller maneuver detection delay at the start of the maneuver,and has a larger maneuver detection delay at the end of the maneuver.It can also be observed that filter 3 has a significant acceleration estimate error than filter 1 and filter 2.This is because filter 3 has a narrower low-pass band that filters out more high frequency estimates.The acceleration estimate error influences the tracking performance of the proposed method significantly.Fig.5(b)and(c)show the position and the velocity estimation errors.When the maneuver occurs at 400 s,the position and velocity estimation errors of the proposed method increase rapidly.Then,the errors of filter 1 and filter 2 decrease and keep lower than the result of UMISE method.However,the state estimation error of filter 3 is not so good because of the long delay of acceleration estimate.In a long period after the beginning and the end of the maneuvering process,the acceleration estimate error of filter 3 is large.In this situation,it is the covariance scaling coefficient that makes the state estimation not diverge.

Fig.7 Tracking performance in Case 3.

In Case 2,the tracking process lasts 3000 s,and the maneuver occurs from 1000 s to 2000 s.The magnitude of the maneuver acceleration is 0.05 m/s and the maneuver is in the direction of satellite’s velocity vector.The main differences between Case 1 and Case 2 are the reduction of the acceleration magnitude and the increase of the maneuvering period,which change the results of filters.

Fig.6 shows the results of the proposed method in Case 2.It can be observed in Fig.6(a)that the acceleration estimate of filter 1 equals zero during the entire tracking process.This is because the maneuver detection threshold of filter 1 proposed in Eq.(11)is larger than the actual maneuver acceleration.It is shown that when the magnitude of the actual maneuver is small,the excessive passband frequency and stopband frequency of the low-pass filter lead to an overlarge maneuver detection threshold(like low-pass filter 1 in Case 2),which causes the proposed method to lose its ability to detect the small maneuver.It can be observed that the tracking performance of filter 1 degrades because of the undetected maneuver,as shown in Fig.6(b)and(c).However, filter 2 and filter 3 still provide good state estimations in this case.The position estimation errors of filter 2 and filter 3 are smaller than UMSIE method during the non-maneuvering period and are almost the same as UMISE method during the maneuvering period.The velocity estimation errors of filter 2 and filter 3 are smaller than UMISE method during the entire tracking process.

In Case 3,the tracking process lasts 5000 s,and the maneuver occurs from 2000 s to 4000 s.The magnitude of the maneuver acceleration is 0.005 m/s and the maneuver is in the direction of satellite’s velocity vector.

Fig.7 shows the results of the proposed method in Case 3.In this case,the magnitude of actual maneuver acceleration is smaller than the maneuver detection thresholds of filter 1 and filter 2,and thus both of these two filters cannot detect the maneuver and provide exactly the same state estimation with a significant estimation error as shown in Fig.7(b)and(c).Filter 3 still provides a good acceleration and state estimation in the tracking process.It is shown in Fig.7(a)that the acceleration estimate of filter 3 is satisfactory.There are large acceleration estimate errors from the beginning of the maneuver to 2200 s and from the end of the maneuver to 4160 s.The acceleration estimate accuracy of filter 3 reaches about 2×10-4m/s2.Because of the accurate acceleration estimate,the state estimation of the proposed method is also good.The position estimation of the proposed method is better than the UMISE method during the non-maneuvering period,and has a similar precision with the UMISE method during the maneuvering period,as shown in Fig.7(b).The velocity estimation of the proposed method is better than the UMISE method during the entire tracking process,as shown in Fig.7(c).

In order to demonstrate the performance of the proposed method more effectively,Monte-Carlo simulations are implemented.Table 3 shows the results of the proposed method in Case 1,2 and 3 in 100 Monte-Carlo runs.

In summary,the proposed method has better tracking performance than the UMISE method when the parameters of the low-pass filter suit the actual maneuver.If the parameters(passband frequency and stopband frequency)are selected too small,the acceleration estimate error is large,which degrades the tracking performance of the proposed method and leads to a large maneuver detection delay at the end of the maneuver,like the results of filter 3 in Case 1.If the parameters are selected too large,the maneuver detection threshold is large,which leads to a decrease in the maneuver detection sensitivity,like filter 1 and filter 2 in Case 3.In this situation,the tracking performance of the proposed method degrades.However,it should be noted that the proposed method still has the robustness of parameters to a certain degree.For example,in Case 1,the magnitude of the actual maneuver acceleration is 0.5 m/s2,while the assumed magnitudes of maneuver acceleration in the low-pass filter 1 and filter 2 are 1 m/s2and 0.1 m/s2.The difference between the assumed and actual value does not affect filter 1 and filter 2 to provide better tracking performance than the UMISE method.Therefore,if there is no priori information about the maneuver,multiple filters with differentparameters proposed in this paper can be used concurrently to obtain a good maneuver estimation and tracking result.

Table 3 RMSE of proposed method and UMISE method in Monte-Carlo simulations.

5.Conclusions

In this paper,a robust extended Kalman filter with input estimation is proposed for tracking maneuvering satellites.The UMISE method provides a rough acceleration estimate with a significant estimation error.With the analysis in the frequency domain,it is found that the acceleration estimate of the UMISE method is close to the actual acceleration at low-frequency part,and the acceleration estimate error is concentrated in the high-frequency part.Therefore,a low-pass filter is used to obtain a more accurate acceleration estimate.Then,the maneuver is detected with a threshold-based approach,which divides the tracking process into the nonmaneuvering period and the maneuvering period.During the non-maneuvering period,the maneuver acceleration is considered as zero,and the state estimation is provided by an extended Kalman filter.During the maneuvering period,the acceleration estimate error is considered as two parts:the fluctuation error and the sudden change error.The fluctuation error is assumed as a random process noise,and the sudden change error is accommodated by a covariance scaling approach.Some Monte-Carlo simulations are used to demonstrate the maneuver tracking capability of the proposed method in different situations.In all simulation cases,the position estimation error of the proposed method is close to that of the UMISE method.However,both the velocity estimation error and the acceleration estimate error of the proposed method are smaller than those of the UMISE method.In 3 simulation cases,the root-mean-square errors of the velocity estimation of the proposed method are about 2–5 times smaller than the results of the UMISE method.The proposed method improves the accuracy of acceleration estimate more significantly.In Case 3,the root-mean-square error of the acceleration estimate of the proposed method is 0.0014 m/s2while the result of UMISE method is 0.7810 m/s2.Moreover,the proposed method provides detection results of maneuver start and end time,which the UMISE method cannot do.

There are also some drawbacks to the proposed method.In this paper,the parameters of the low-pass filter need to be determined in advance by an assumed maneuver acceleration instead of being determined adaptively.If there is a large difference between the actual maneuver and the assumed value,the performance of the proposed method degrades.Besides,the proposed method can accommodate the slowly changing maneuver acceleration.If the variation of the maneuver acceleration is very severe,the low-pass filtering method may filter out the high-frequency part of the actual acceleration,and it may reduce the tracking performance of the proposed method.Overcoming these drawbacks and improving the maneuver tracking performance will be our future work.

Acknowledgement

This research is supported by the National Natural Science Fund for Distinguished Young Scholars of China(No.11525208).