Subsonic impulsively starting flow at a high angle of attack with shock wave and vortex interaction
2018-09-27ChenyuanBAIJuanLIZiniuWU
Chenyuan BAI,Juan LI,Ziniu WU
School of Aerospace Engineering,Tsinghua University,Beijing 100084,China Institute of Aeroengine,Tsinghua University,Beijing 100084,China
KEYWORDS Advance of stall;Compressible vortex;High angle of attack;Subsonic starting flow;Unsteady shock waves
Abstract Impulsively starting flow,by a sudden attainment of a large angle of attack,has been well studied for incompressible and supersonic flows,but less studied for subsonic flow.Recently,a preliminary numerical study for subsonic starting flow at a high angle of attack displays an advance of stall around a Mach number of 0.5,when compared to other Mach numbers.To see what happens in this special case,we conduct here in this paper a further study for this case,to display and analyze the full flow structures.We find that for a Mach number around 0.5,a local supersonic flow region repeatedly splits and merges,and a pair of left-going and right-going unsteady shock waves are embedded inside the leading edge vortex once it is sufficiently grown up and detached from the leading edge.The flow evolution during the formation of shock waves is displayed in detail.The reason for the formation of these shock waves is explained here using the Laval nozzle flow theory.The existence of this shock pair inside the vortex,for a Mach number only close to 0.5,may help the growing of the trailing edge vortex responsible for the advance of stall observed previously.
1.Introduction
Starting flow is caused by a sudden change of the angle of attack or forward speed of an airfoil,and is of primary importance in aeroelasticity(which involves step motion1),vehicle maneuverability2,3(which involves fast movement of command surfaces),and wing-gust interaction4(which is equivalent to attain a finite angle of attack).
For a small angle of attack,a linear theory has been developed for incompressible staring flow by Wagner4and Walker5,for supersonic starting flow by Heaslet and Lomax6,and for subsonic flow by Lomax et al.7A time-dependent analytical lift force coefficient has been obtained for these cases.For the incompressible case,Wagner’s solution shows that the initial lift is one half of its steady state value and increases monotonically with time following a curve known as the Wagner function.This force variation is due to a gradual build-up of the boundary vorticity and a free vortex sheet from the trailing edge.For supersonic flow,the solution of Heaslet and Lomax predicts a force plateau for small time,and this force then increases in time,reaching to the steady state value for large time.This force variation comes from interaction between steady and unsteady Mach waves below and above the airfoil.
For incompressible staring flow at a large angle of attack,vortex spirals form from both the sharp leading edge and the trailing edge,which,by close interaction with the airfoil,cause an initial singularity of lift8,and this singularity is then released when the vortex spirals are blown off the airfoil.After a force-increasing stage,stall occurs due to interaction between leading and trailing edge vortices.
An analytical solution has been found by Bai and Wu9,10for supersonic and hypersonic starting flows at a large angle of attack.In this case,a steady shock wave and an unsteady shock wave form on the windward side of an airfoil,and their interaction leads to a secondary wave which grows in time.A steady Prandtl-Meyer wave and an unsteady rarefaction wave form on the leeward side of the airfoil,and their interaction also forms a secondary wave growing in time.A further study shows that inside the secondary wave on the leeward side,there is a left-going shock wave.11
If we look at the connection between the flow structure and the force behavior for starting flow at a high angle of attack,it may be concluded that for incompressible flow,the force behavior is dominated by vortex flows,while for supersonic flow,this is dominated by compressible flows.However,it is special for subsonic starting flow where both vortices and compressible waves may be important.The subsonic flow problem may be further complicated by interaction between compressible waves and vortices.This interaction may be pronounced at an intermediate Mach number between zero and one.
Indeed,a preliminary study for subsonic starting flow at a large angle of attack12shows that stall is advanced at one Mach number,i.e.,stall for a large angle of attack occurs at a time earlier than other Mach numbers.It is therefore required to look at what happens at this particular Mach number.
We therefore display in this paper the flow details for subsonic starting flow at that Mach number and at an angle of attack.The particular flow structure will be analyzed.Notably,we will examine whether there are shock waves embedded in the vortex flow structure that may be responsible for the observed lift evolution behavior with advance of stall.
Such a study not only enriches knowledge about the flow structure of subsonic starting flow at a high angle of attack,but also offers a possibility to observe in real applications whether shock waves appear inside a compressible vortex,a phenomenon anticipated using a simple vortex pair model.13,14The simple vortex pair model is for steady flow,and here in the present case,the flow is unsteady,so the phenomenon is more complex.
In Section 2,we will demonstrate numerical results of the flow structure.In Section 3,we will perform an analysis of the flow structure observed.Section 4 shows the detailed history of shock formation.Conclusions are provided in Section 5.
2.Numerical results of subsonic starting flow
As usual for study of starting flow,we use the nondimensional time defined by

This non-dimensional time measures the number of chords traveled at time t by an airfoil of a chord length cAand travelling at a constant speed V∞.
Fig.1 displays the lift force evolutions in time for subsonic starting flow at various Mach numbers and for an angle of attack α =20°.For incompressible flow(zero Mach number),stall occurs after the airfoil travels about 4 chord lengths,i.e.,at τ≈ 4.For a Mach number Ma∞=0.8,stall occurs at τ≈ 3.4.For a Mach number of 0.5,stall occurs at τ≈ 3.0.Thus,for a Mach number around 0.5,stall occurs earlier than for other Mach numbers,whether they are higher or lower than 0.5.This would mean that something new appears in the flow structure for a Mach number around 0.5.
To see what happens,we display the streamlines,Mach contours,and pressure contours for several typical instants and computed numerically by CFD,for Ma∞=0.5 and α =20°.
The flow is computed using a body- fixed frame,in which the airfoil is held fixed.A uniform flow with the given angle of attack is set initially.Once computation is started,the application of a non-penetrating condition along the wall of the airfoil builds vorticity and compressible waves near the wall.
The present study only considers inviscid flow.We thus solve the full set of nonlinear Euler equations in gas dynamics.For numerical simulation,we use the same approach as used before for a similar problem.9,10The grid is refined as before to have a grid-converged solution(see Appendix C in Ref.10for details).Precisely,we use the well-known Roe scheme based on finite difference approximation and second-order upwinding for the flux.The Fluent code incorporating these CFD approaches is used.This approach has been quantitatively verified using known analytical solutions,including the linear solution of Heaslet-Lomax supersonic starting flow problem in Ref.10and the Wagner incompressible flow model in Refs.15,16.

Fig.1 Lift curves for starting flow of flat plate at several Mach numbers(angle of attack α =20°),showing that stall occurs earlier at a Mach number of 0.5(The data comes from Ref.12).
Fig.2 displays streamlines at instants τ=0.5,τ=3.0,and τ=3.75.We observe that the leading edge vortices continu-ously grow and then get detached.A concentrated trailing edge vortex starts to form at τ=3.0.The appearance of a new concentrated trailing edge vortex has been explained to be the reason of stall.15,16According to Fig.2,a trailing edge vortex occurs at the same instance(τ≈ 3.0)as that of the stall.Hence,stall can still be associated with the appearance of the concentrated trailing edge vortex,as for incompressible flow.This means that the advance of stall is due to the advance of the appearance of the concentrated trailing edge vortex.This indicates that the leading edge vortex should have some particular properties,since it is the approaching of the leading edge vortex to the trailing edge that triggers out the trailing edge vortex.
Fig.3 displays the Mach number and pressure contours for τ=0.5,τ=3.0,and τ=3.75.We observe two shock waves at τ=3.0.The detailed history of the appearance of the shock waves will be studied in the next section.At τ=3.75,the lower shock becomes a lambda shock.
To see the relative positions of these two shock waves with respect to the leading edge vortex,we display in Fig.4 the Mach number contours and streamlines for τ=3.0,3.75.Hence,for τ=3.0,the lower shock(Sb)is at the bottom left part of the vortex,and the upper shock(Su)is at the top right part of the vortex.The lambda shock at τ=3.75 comes from the merging of the original shock Suwith a similar upper shock created at the top of the trailing edge vortex.
This observation has the following significances.
(1)First of all,a shock wave inside a compressible vortex has been theoretically predicted by previous model studies.13,14However,the previous model studies used a simple vortex pair model for steady flow.Here in the present case,the flow is unsteady,so the phenomenon is more complex.
(2)Previous studies predicted only one shock wave.For instance,Heister et al.14only showed a shock wave on the top of the vortex.Here,we observe two unsteady shock waves,one on the top as predicted by Heister et al.14and the other on the bottom(Sb).In the next section,we will explain the reason why the bottom shock wave appears.
(3)The observation of the formation of a lambda shock wave between the main vortex and the trailing edge vortex is also new here.
(4)The appearance of shock waves certainly changes the position and strength of the leading edge vortex,compared to a case without shock waves.This may be the cause that the appearance of the trailing edge vortex is advanced at Ma∞=0.5,which then advances the stall.
3.Analysis of shock waves inside compressible vortex
In this section,we present the shock expressions for left-and right-going shock waves,and check which family the two shock waves belong to.Then we discuss the reason for the formation of the shock waves.
The shock phenomenon observed here is essentially onedimensional,so we only consider a one-dimensional study.Let ρ,p,u,a,Ma be the density,pressure,velocity,sound speed,and Mach number.We use subscripts l and r to denote status left and right to the shock wave,respectively.The basic expressions for an unsteady shock wave can be found in the paper of Gottlieb and Groth.17
For a left-going shock wave(also called the first family),the shock speed is given by
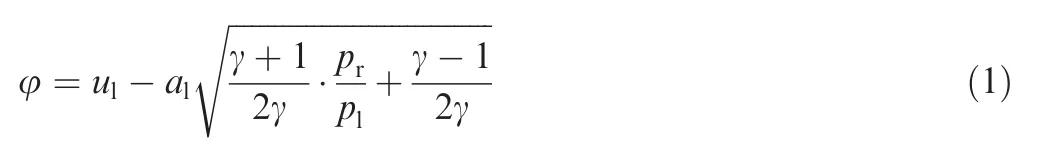
and the velocity and pressure are related by

For a right-going shock wave(also called the second family),the shock speed is given by
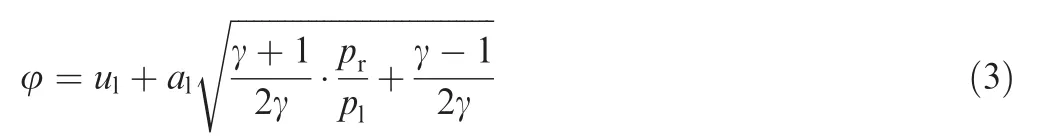
and the velocity and pressure are related by

To check which family each shock embedded in the vortex belongs to,we pick up the data pl,pr,al,ulfrom the CFD solutions,and compute urand φ using the theoretical expressions above.If urand φ predicted by Eq.(1)and Eq.(2)match the CFD results,then that shock wave belongs to the first family(left-going shock wave).If urand φ predicted by Eq.(3)and Eq.(4)match the CFD results,then that shock wave belongs to the second family(right-going shock wave).

Fig.2 Streamlines at several instants(τ=0.5,3.0,3.75)displaying the evolutions of leading and trailing edge vortices for subsonic starting flow at Ma∞ =0.5 and α=20°.
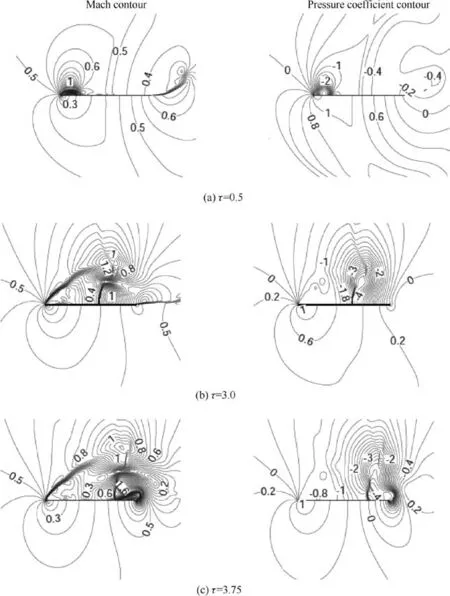
Fig.3 Mach contours at several instants displaying two shock waves for subsonic starting flow at Ma∞ =0.5 and α =20°.

Fig.4 Mach contours and streamlines displaying the positions of shock waves inside the leading edge vortex,for subsonic starting flow at Ma∞ =0.5 and α=20°.

Table 1 Shock types for the bottom and top shock waves embedded in the vortex,τ=3.0.
A comparison is given in Table 1.Since the theory used is one-dimensional while the real flow is two-dimensional,the comparison between theory and CFD results cannot be exact,but is good enough to draw conclusions that the shock wave at the bottom of the vortex(Sb)is a right-going shock wave(second family)while that at the top(Su)is a left-going shock wave( first family).
Now we explain the reason why shock Sbappears.The reason that Suappears follows from the same reason as explained by Heister et al.14For simplicity,we only perform a qualitative study.For the compressible vortex above the plate,there is an image vortex below the plate(see Fig.5 for illustration).It is clear that the streamlines between the vortex cores of the real and image vortices form an equivalent Laval nozzle.
For Laval nozzle flow and within the context of a quasione-dimensional flow model,there is a pressure condition so that the throat is sonic,and downstream from the sonic throat there is a shock wave.
Let Atbe the area or height of the throat and Aethe area or height at the exit of the throat.In case of a sonic throat and isentropic flow throughout the nozzle,the Mach number at the exit Maeis related to the area ratio At/Aeby the quasione-dimensional flow relation as


Fig.5 Schematic diagram for the generation of the shock wave.The compressible vortex above the plate has an image vortex,so there is an equivalent Laval nozzle between the cores of the real and image vortices.
Still for isentropic flow,the pressure at exit peis related to the Mach number at the exit Maeby

where p0is the total pressure at the inlet.
For a given area ratio At/Ae,Eq.(5)predicts two Mach numbers Mae,I,Mae,II,with Mae,I< 1(subsonic out flow)and Mae,II> 1(supersonic out flow).Inserting these two Mach numbers into Eq.(6)gives two exit pressures pe,I,pe,II,with pe,II< pe,I.If the ambient pressure at the exit is lower than pe,Ibut sufficiently close to pe,I,then there is a shock wave inside the divergent part of the nozzle.
As displayed in Fig.4,for τ=3,the flow is indeed sonic(Ma=1)at the throat(R1).Downstream(here on the lefthand side since the flow direction is leftward at the bottom of the vortex)from the sonic throat,the flow is supersonic according to Fig.4.The shock Sbthus follows from the mechanism of the formation of a shock wave inside a Laval nozzle as discussed above.Note that the theory for a Laval nozzle is a steady-state model,while Sbis an unsteady shock wave based on a body- fixed frame.If we choose a reference frame moving with the vortex,then the steady-state theory can be applied to the present case.
4.Detailed history of formation of shock waves
To see how shock waves appear inside the leading edge vortex,we display in Fig.6 the Mach contours(with a partial display of streamlines showing the leading edge vortex)at six different instants.
At τ=0.5,where the core of the leading edge vortex is roughly at 0.12cAdownstream from the leading edge,we observe two supersonic flow regions,one at the bottom of the vortex and the other at the top.The flow is smooth between the supersonic flow region and the subsonic flow region,so there is no shock wave at this instance.
At τ=0.89,where the core of the leading edge vortex is roughly at 0.22cAdownstream from the leading edge,the two supersonic flow regions are enlarged.Still,there is no shock wave.
At τ=0.92,the supersonic region at the top of the leading edge vortex is in time to be split into two supersonic regions.
At τ=0.96,the supersonic region at the top of the leading edge vortex is completely split into two supersonic regions.This is the instant near which shock waves erect from the edges of supersonic regions.This becomes clearer at τ=1.2.

Fig.6 Mach contours and streamlines at six difference instants,showing the appearance of shock waves.
At τ=1.2,a left-going shock wave stands on the left edge of the bottom of the leading edge vortex,and a right-going shock wave stands on the right edge of the top of the leading edge vortex.Surprisingly,the broken supersonic flow region merges again at this instance.
At τ=1.64,the existences of a left-going shock wave below the leading edge vortex and a right-going one above the leading edge vortex are very clear.
Hence,shock waves do not form at the very initial period of time.They form only after the leading edge vortex has sufficiently grown up.Moreover,the supersonic region at the top of the leading edge vortex experiences a splitting and merging evolution during the period that shock waves appear.
5.Conclusions
We have studied subsonic starting flow for a Mach number of 0.5 and an angle of attack of 20°.We observe two shock waves inside and travelling with the time-growing vortex that shed from the leading edge.
We have shown that the shock wave at the bottom of the vortex is a right-going shock wave and the one at the top of the vortex is a left-going shock wave.Shock waves do not form at the very initial period of time but after the leading edge vortex has sufficiently grown up.Moreover,the supersonic region at the top of the leading edge vortex experiences a splitting and merging evolution during the period that shock waves appear.
This study complements previous studies of starting flow at a high angle of attack,which are only for incompressible or supersonic flow.Moreover,the observation of two shock waves enriches the previous knowledge of a compressible vortex pair having the possibility of one shock wave,according to theoretical studies.Moreover,the advance of stall observed only for a Mach number of around 0.5 may be due to the appearance of these shock waves triggering out the formation of a stall-inducing trailing edge vortex at much early time.For Mach numbers much greater than 0.5(say for instance 0.8),no shock waves inside the vortex are observed,and stall occurs at later times.
In the present study,we only considered inviscid flow.As discussed in Ref.17for incompressible flow,the effect of viscous transportation in real flow is minor.This is due to the fact that for a large angle of attack,the flow is dominated by large vortices separated from leading and trailing edges.In fact,Wang18and Nitsche and Xu19already noticed the insensitivity of intensity of large-scale vortices to the Reynolds number for large-angle of attack flow.Notably,Nitsche and Xu19stated that the major contribution to circulation of the leading edge vortex is inviscid convection of shed vorticity into the vortex region,and at early times,the total shed circulation is highly independent of the Reynolds number.In the future,we will check how flow details are affected by viscosity.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(No.11472157).
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- 80 years education of aerospace science and technology in Tsinghua University
- A brief overview of the School of Aerospace Engineering of Tsinghua University
- Detached-eddy simulation of supersonic flow past a spike-tipped blunt nose
- High-order compact finite volume methods on unstructured grids with adaptive mesh refinement for solving inviscid and viscous flows
- Pressure distribution guided supercritical wing optimization
- A high- fidelity design methodology using LES-based simulation and POD-based emulation:A case study of swirl injectors
