High-order compact finite volume methods on unstructured grids with adaptive mesh refinement for solving inviscid and viscous flows

Jianhua PAN,Qian WANG,Yusi ZHANG,Yuxin REN

School of Aerospace Engineering,Tsinghua University,Beijing 100084,China

KEYWORDS Adaptive mesh refinement;Compact stencil;High-order finite volume scheme;Unstructured grids;Variational reconstruction

Abstract In the present paper,high-order finite volume schemes on unstructured grids developed in our previous papers are extended to solve three-dimensional inviscid and viscous flows.The high order variational reconstruction technique in terms of compact stencil is improved to reduce local condition numbers.To further improve the efficiency of computation,the adaptive mesh refinement technique is implemented in the framework of high-order finite volume methods.Mesh refinement and coarsening criteria are chosen to be the indicators for certain flow structures.One important challenge of the adaptive mesh refinement technique on unstructured grids is the dynamic load balancing in parallel computation.To solve this problem,the open-source library p4est based on the forest of octrees is adopted.Several two-and three-dimensional test cases are computed to verify the accuracy and robustness of the proposed numerical schemes.

1.Introduction

High-order numerical schemes have shown great potentials in solving multiscale problems in fluid dynamics such as turbulence and vortex-dominated flows.To solve practical problems with complicated geometries,high-order numerical methods on unstructured grids have been extensively studied in the past two decades.Representative numerical methods include the Discontinuous Galerkin(DG)method,1,2the PNPMmethod,3the RDG method,4the DG/FV method,5the Residual Distribution(RD)method,6Spectral Volume(SV)7or Spectral Difference(SD)8methods,and the Correction Procedure via Reconstruction(CPR)method.9

Historically,High-order finite Volume(FV)methods10–14on unstructured grids were among the numerical schemes that received earliest attentions,since they are simpler to construct and implement.Shock-capturing algorithms and implicit time stepping techniques for high-order FV schemes are also more mature than those of the numerical methods mentioned above.However,high-order FV schemes require a large number of cells or control volumes in the stencil of the reconstruction procedure.The large stencil results in a series of problems6including cache missing due to the data in the stencil being far away in memory,difficulty in boundary treatments,and deterioration of the parallel efficiency.Therefore,a very large stencil has been one of the most serious problems for highorder FV schemes.

To solve this bottleneck problem,the authors of the present paper have proposed two new reconstruction procedures,namely the Compact Least Squares Reconstruction(CLSR)15,16and the Variational Reconstruction(VR).17The common feature of these two methods is that they can reconstruct arbitrarily high-order polynomials using a compact stencil involving only face-neighboring cells.The VR is superior to the CLSR in that the reconstruction is always non-singular and does not need to reduce the order of accuracy at boundary cells.FV schemes based on the VR presented in Ref.17are for two-dimensional problems.In the present paper,this method is extended to solve three-dimensional problems.More importantly,in the present paper,a new cost function(functional)is proposed in the VR,which can significantly reduce the condition number of the reconstruction procedure and improve the robustness of the scheme.

To further enhance the efficiency of the proposed numerical methods,the compact high-order FV methods are combined with the grid adaptation technique.As being pointed out in Ref.18,‘‘Observing design-order asymptotic spatial and temporal convergence rates through grid adaptation that are independent of the initial grid can dramatically improve the confidence in a simulation method and application.”The use of high-order methods in the grid adaptation technique can further improve the accuracy of simulation and reduce the total number of grids.Adaptive Mesh Refinement(AMR)techniques are a general class of grid adaptation methods,19which can be based on block-structured grids,20unstructured grids,21,22and grids with tree data structures.23,24In the present paper,we focus on tree-based AMR methods,since grid refinement/coarsening is easy to implement in this case.This feature is very important for unsteady flow computations where grid adaptation should be performed many times during simulations.

Two main ingredients of the AMR algorithm are error indicators and the strategy to refine and coarsen the mesh.18Error indicators have been studied extensively,but there are still many issues yet to be solved.25–27In the present paper,we focus on error indicators based on flow structures,for example,indicators for shock wave,entropy transport,and vortices.The advantages of these indicators are that they are very simple and suitable for both steady and unsteady flows.Grid refinement or coarsening is based on the tolerances to the local error indicators.Another important issue of the AMR algorithm is the load balance in parallel computation.In the present paper,the framework for parallel computation and load balance is based on the p4est19,28software library.The p4est provides a set of scalable parallel algorithms that strictly adheres to distributed encoding and storage of the forest-of octree,which have scalable mesh handling capabilities for general numerical simulations.In the present paper,fourth-order FV schemes based on the VR are combined with the p4est.To our knowledge,this is the first attempt to implement highorder FV schemes with a compact stencil in the p4est framework.In this paper,several two-and three-dimensional test cases are solved using AMR FV schemes based on the VR.Numerical results show that the present method can predict these problems with high accuracy and efficiency.

The rest of the paper is organized as follows.High-order FV schemes based on the VR are presented in Section 2.The AMR technique and the incorporation of the high-order FV schemes are introduced in Section 3.Section 4 reports results of numerical test cases.Finally,conclusions are given in Section 5.

2.Numerical schemes

2.1.Finite volume schemes

In the present paper,the governing equations are threedimensional compressible Navier-Stokes equations,which can be written in a conservation form as

where U is the vector of conservative variables;Fc,Gc,and Hcare the inviscid fluxes;Fv,Gv,and Hvare the viscous fluxes.Their specific forms are well known and thus omitted.We assume that the flow is Newtonian,and use the equation of state of ideal gases to close the governing equations.

The equations are solved using the FV method.The computational domain Ω is subdivided by N non-overlapping control volumes,and the ith one is denoted as CVi,i.e.,

The volume of the control volume CViis denoted as Vi.Integrating Eq.(1)over a control volume and applying the Gauss Theorem,one obtains

where f is the surface of the control volume,s stands for the sth Gaussian quadrature point for the surface integral,Wf;sis the corresponding weight of the Gaussian quadrature rule,and n is the outward unit normal vector at point s.In Eq.(2),is the vector of the cell averages of the conservative variables defined by

and I is the flux tensor given by

where e1,e2,and e3are the unit base vectors of the Cartesian coordinates.

It is well known that the implementation of FV schemes consists of the following three steps.29

The first step is the reconstruction,in which a piece-wise polynomial is recovered from the cell averages U-iof all control volumes∀CVi∈ Ω.This is a necessary step since the dependent variables obtained in FV schemes are the cell averages of the conservative variables.It is particularly important for highorder FV schemes for which piece-wise high-order polynomials must be reconstructed.

The second step is the evolution step,in which the normal flux I·n is computed by a certain Riemann solver or flux splitting technique.Point s in Eq.(2)is on the surface of CViwhich is the interface between the control volume CViand a faceneighboring control volume denoted by CVj.Denoting Ui(x)and Uj(x)as the piece-wise polynomials obtained in the reconstruction step,the left and right states at the interfacial point s can be computed by UL=Ui(xs)and UR=Uj(xs).ULand URare not identical in general.To compute the numerical flux(superscript*indicates that the numerical flux is an approximation of the exact flux),one should deal with the inviscid fluxand the viscous fluxboth with discontinuous left and right states.The computation of these flux terms will be further introduced in Section 2.3.

The third step is the projection step,in which Eq.(2)is temporally advanced by a time-stepping scheme so thatis obtained fromfor∀CVi∈ Ω.The time-stepping scheme will also be briefly introduced in Section 2.3.

2.2.Variational reconstruction

The reconstruction is an important and challenging procedure in high-order finite-volume schemes on unstructured grids.For simplicity,we assume that u( x)is a component of U( x，t)in Eq.(1)at a given time tn.The reconstruction procedure in the FV scheme can be stated as follows.Knowing the cell average as

on all control volumes∀CVi∈ Ω,we find a piece-wise degree k polynomial defined on CViin the form of

that approximates u( x)to( k+1)th order of accuracy.In Eq.(3),is the unknown coefficient to be determined,and φil(x)is the zero-mean polynomial basis.The zero-mean polynomial basis is a modification of the standard polynomial basis so that the cell average ofon CVisatisfies

This relation guarantees the conservation of Eq.(4),i.e.,The detailed formulation ofcan be found in Refs.16,17.For a degree k polynomial,the number of unknown coefficientsis

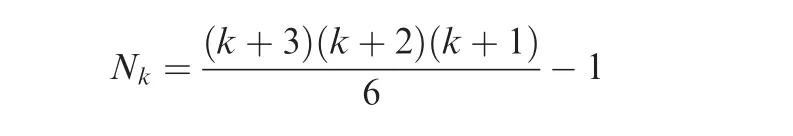
for three-dimensional problems.With an increase of k,the number of unknown coefficients increases very fast.For example,for the linear reconstruction,Nk=3,and for the cubic reconstruction(k=3),the number of unknowns is Nk=19.Therefore,at least 19 cells or control volumes must be included in the reconstruction stencil to determine the unknowns in the k-exact reconstruction.Furthermore,the matrix of the reconstruction may be singular.To remove the similarity and improve the stability of the schemes,it is recommended that the reconstruction stencil should have a number of cells at least 1.5 times of the number of unknowns,30which means that for the cubic reconstruction,at least 28 cells should be used.The large stencil is a serious problem for high-order FV schemes,which will reduce the computational efficiency especially in parallel computing and bring difficulties in designing highorder treatment of boundary conditions.

To overcome this deficiency,the VR has been presented in Ref.17.In the present paper,an improved reconstruction strategy is proposed to further improve the robustness of the VR.The basic idea of the VR is to compute the unknown coefficientsby asking Eq.(4)to minimize a cost function(functional)using the direct variational approach.The properties of the reconstructed polynomial are therefore closely related to the specific form of the functional.In the present paper,the functional is

is the Interfacial Jump Integration(IJI)function.In Eqs.(5)and(6),subscript f stands for the fth surface shared by control volumes CVL=CViand CVR=CVj,i.e.,

and| SLR|is the area of SLR.ωLRis the weight of surface SLR.andare the scaling factors to make all terms in the summation to have the same dimension,in which Δxi=max( xε)-min( xε),Δyi=max( yε)-min( yε), and Δzi=max( zε)-min( zε),where subscript ε stands for each of the vertex of the control volume CVi.

To compute the unknown coefficients in Eq.(4),we substitute pi(x)=pL(x)and pj(x)=pR(x)into Eq.(6),and minimize J by requiring

In Eq.(7),only Jfwith its one neighboring cell being CViwill have none-zero terms.In other words,Eq.(7)is only related to the information on CViand its face-neighboring cells.Therefore,the reconstruction relation Eq.(7)uses a compact stencil.For illustration purpose,the stencil for a two dimensional problem is shown in Fig.1 although the numerical methods discussed in the present paper are for threedimensional problems.The stencil is denoted as STi,and for the case shown in Fig.1,

Fig.1 Compact stencil for two-dimensional reconstruction.

After defining the reconstruction stencil,Eq.(7)can be written as

The above equations can be written locally in a matrix form as

Over all control volumes,Eq.(8)can be assembled into a large system of linear equations.It can be proven that there exists a unique solution for this system of equations,since the corresponding matrix is symmetric and positive definite.The proof is omitted here for brevity.Interested readers can refer to Ref.17for more details.It should be noticed that although the cost function of the present paper is different from that in Ref.17,the proof is basically identical.The solution of Eq.(8)will give the unknown coefficients in Eq.(4),and therefore reconstructed polynomials on all control volumes can be obtained.

If Eq.(8)is solved in its assembled form using a direct solver,it requires very large amount of the computation,and the procedure is by no means compact.In the present paper,the approach in Refs.16,17is adopted where an iterative solver is used to maintain the compactness of the solution procedure.The ‘‘compactness” used in the present paper is in the sense that in any single operation,we only use the information of current and face-neighboring cells,which is called ‘‘operationally”compact in Ref.17.The simplest iterative solver is the block-Jacobian solver which reads as

where r is the index of iteration.A use of the Gauss-Seidel technique with over relaxation can significantly improve the convergence rate.To further improve the efficiency,a reconstruction and time integration coupled iteration method16is used in the present paper.A few more details will be given in the next subsection.

It should be emphasized that the main difference between the current method and the method proposed in Ref.17is the cost function for driving reconstruction relations.Since the present reconstruction procedure will be used in the AMR framework where multi-level grids grouped into the forestof-octree will be used as the input of the reconstruction,it is crucial for the reconstruction procedure to be as robust as possible on unstructured grids with large variations in both the size and aspect ratio.One criterion to measure the robustness of the reconstruction procedure is the local condition number of Eq.(8)which is defined as the ratio between the largest and smallest eigenvalues of Aiiin their absolute values.Fig.2 shows a comparison of local condition numbers between the present method and the method of Wang et al.17on the grid provided in Ref.31.This grid is known to have a very large aspect ratio and skewness.According to Fig.2,the local condition number of the present method is about three orders smaller than that in Ref.17,which indicates that the present method is more robust in treating low-quality grids.This advantage is of crucial importance in designing high-order numerical methods for AMR applications.

2.3.Implementation of numerical methods

The numerical methods of the present paper are basically a three-dimensional extension of those presented in Ref.17with improved reconstructions.The implementation of the numerical methods can be also found in Ref.17.To be complete,we point out that the inviscid flux is computed by the Roe Riemann solver,32the viscous flux is computed by the method presented in Ref.17,a reconstruction and time integration coupled iteration method is adopted to improve the efficiency of the numerical methods,and a limiter based on the Weighted Biased Average Procedure(WBAP)33and the secondary reconstruction33is used in simulations for flow with shock waves.Additional details are given in the following remarks.

Fig.2 Local condition number,with the horizontal axis indicating different control volumes.

Remark 1.For unsteady flow simulations,the time integration scheme should also be in a high order of accuracy.In the present paper,the third-order implicit Runge-Kutta ESDIRK S4P3 scheme34is used.The characteristic of this scheme is that the flow variables as well as the reconstruction coefficients at time tn+1can be obtained directly in the last Runge-Kutta step.This feature is very important when the AMR technique is applied,where a reconstruction at tn+1is needed in giving the initial values for the new cells generated by subdivision of their parent cells.On the other hand,if the implicit Runge-Kutta scheme adopted in Ref.17is used,the flow variables at time tn+1should be computed by a linear combination of the flow variables in previous Runge-Kutta steps.Although this technique can be also applied to the coefficients of the reconstruction polynomials,additional computation and storage are needed.

Remark 2.The present high-order numerical schemes are implemented on high-order grids to ensure a high-order accuracy near the boundaries.A typical high-order control volume is shown in Fig.3.The iso-parametric transformation is used to transform the control volume into a cube with a unit length in a parametric space,and a numerical quadrature is carried out in the parametric space.When the control volume is near the solid walls,the control points defining the iso-parametric transformation of the boundary surface are extracted from the geometry.This procedure ensures a high-order representation of the solid walls which guarantees a high-order accuracy of the numerical schemes near the wall boundaries.The highordergrid generator Meshcurve35is used to generate high-order grids.It should be emphasized that the generated high-order mesh is shape-preserving as shown in the 3rd,4th,and 5th examples in Section 4.

3.Adaptive mesh refinement

3.1.Overview

Fig.3 High-order grids and the iso-parametric transformation.

To implement the AMR technique,one needs to firstly generate a baseline grid.In the present paper,the baseline grid is an unstructured hexahedral grid which is flexible enough to handle complex geometries.Each cell or control volume can be subdivided into eight smaller cells,and one or more of the eight cells can be further subdivided in a recursive manner.A two-dimensional view of this procedure is shown in Fig.4,where a hatched cell is subdivided into 4 cells with one of them is further subdivided.To determine which cells should be subdivided,a refinement criterion is needed.There are also cases that already subdivided cells(8 in a 3D case and 4 in a 2D case)need to be combined into one cell if the local flow field is smooth enough according to the grid coarsening criterion.Furthermore,to avoid grid singularity,it is also required that the grid should be 2:1 balance,28which means that the difference of the subdivision levels between two adjacent cells should be smaller than 2.Therefore,the AMR procedure may involve rather complicated data structures and grid operations.

To show this more clearly,the detailed two-dimensional grid refinement and coarsening process is depicted in Fig.5.Fig.5(a)is the grid after certain steps of computation,which is served as the initial grid for current grid refinement and coarsening operations.We firstly use the grid coarsening criterion to determine which cells should be coarsened.In the present case as shown in Fig.5(b),cells 3,4,5,and 6 of the initial grid should be coarsened and combined into one larger cell.The second step is the grid refinement.In Fig.5(c),cell 33 of the initial grid is divided into four smaller cells.After the grid refinement,there are some cells that are not in 2:1 balance.For example,cell 34 in Fig.5(c)is four times as large in length as its adjacent cells(33,1)and(33,3).In the balancing procedure shown in Fig.5(d),cell 34 is subdivided to ensure the 2:1 balance.

To handle such a complicated process efficiently and more importantly to achieve the dynamic load balance in parallel computing,the open-source library p4est19,28is used in the present paper.The p4est provides scalable algorithms for parallel AMR based on the forest-of-octree approach.In the p4est,the baseline mesh is called the macromesh.28Each cell of the macromesh can be subdivided recursively to form an octree where each node(a microcell)either is a leaf or has eight children.The tree nodes are called octants,and the root of the tree is a cell of the macromesh.A collection of all octrees forms a forest-of-octree.

The p4est provides a number of high-level algorithms to handle the grid refinement,coarsening,and 2:1 balancing process.19,28Therefore,by using the p4est,the process in Fig.5 can be carried out automatically.The p4est also provides mesh connectivity and neighborhood relations which can be used in the present numerical methods to determine the reconstruction stencil and to treat the boundary conditions.These relations are computed using an integer-based algorithm to avoid topological errors due to roundoff.

Fig.4 Baseline grid and subdivision of a hatched cell.

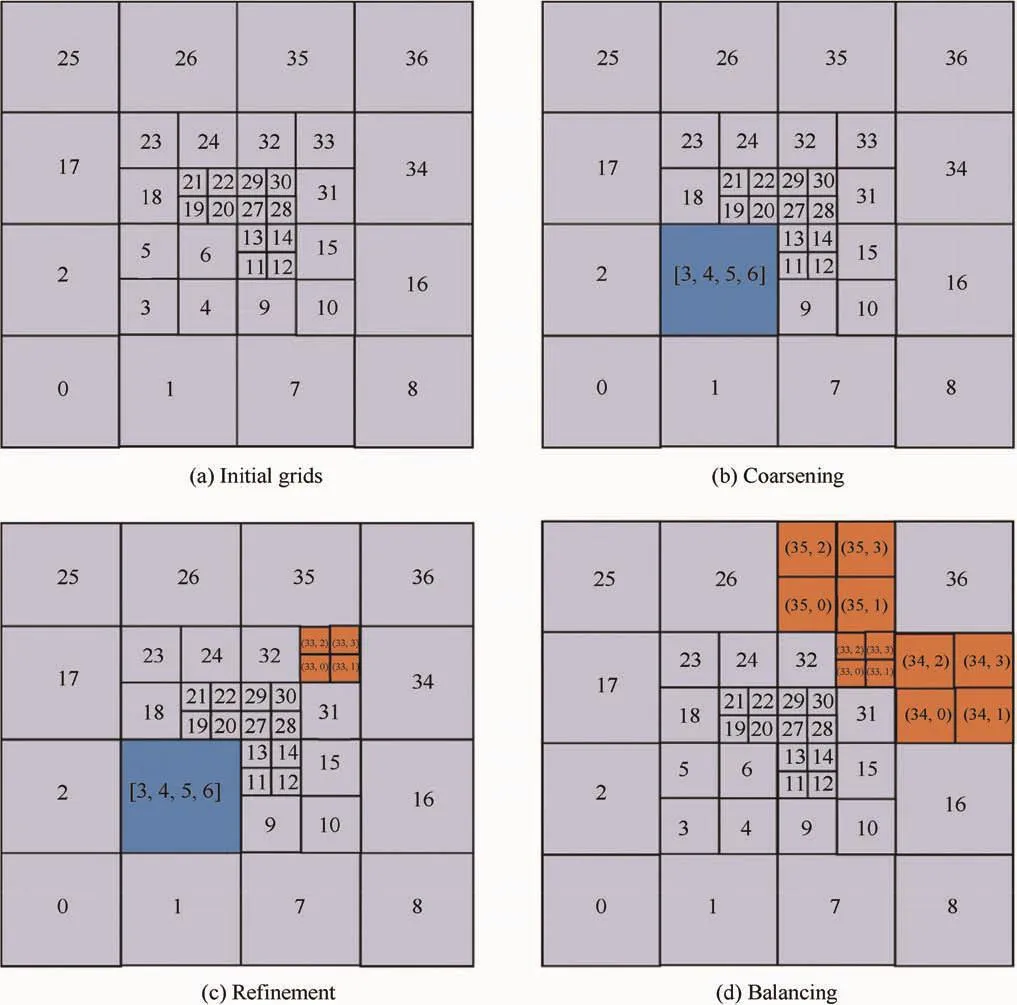
Fig.5 Adaptive mesh refinement procedure.

One outstanding issue in the parallel implementation of the AMR technique is to maintain the load balance.It is particularly important in unsteady flow simulations,since the grid refinement and coarsening process needs to be carried out frequently.There have been some software packages such as parMetis36and Zoltan37dealing with such an issue.However,the domain decomposition approaches used in such software packages are computationally expensive.The p4est presents an efficient load balancing algorithm that strictly adheres to distributed encoding and storage of the forest-of-octree,which is more flexible than a similar approach that replicates the mesh storage in each process and is very efficient.28

The load balancing algorithm of the p4est is based on the globally node numbering and ordering technique.This technique is a two-level ordering approach.The first level is to order the cells of the macromesh by hand or by directly using the numbering given by mesh generation software.The second level is the ordering of cells within an octree,which is achieved using a space- filling z-shaped curve in the geometric domain(z-ordering).28The second-level ordering is imbedded into the first level to form a total ordering of all octants in the domain.The ordering scheme and the space- filling z-shaped curve are shown in Fig.6 for a two-dimensional case.With this unique ordering,the dynamic load balance is achieved by a parallel partition which is created by dividing the curve of ordering into p segments with p being the number of parallel processes.This algorithm is very efficient,and has been implemented in parallel computing using up to 220000 CPU cores.28

3.2.Numerical methods for AMR applications

The numerical schemes described in Section 2 can be extended to the framework of the AMR straightforwardly.The AMR technique presented in the previous subsection produces a typical multi-level local grid as shown in Fig.7 for a two dimensional view.The central control volume CViis a control volume with hanging nodes.Unlike the traditional finite element approach,there is no difficulty in treating a cell with hanging nodes for the FV scheme.For example,CVican be treated as a control volume with f1，f2，...，f6as its interfaces,and numerical fluxes are evaluated on each of these interfaces.

Fig.6 Ordering scheme and the space- filling z-shaped curve.28

The reconstruction procedure must also take the hanging nodes into consideration by including the IJI of Jf1，Jf2，...，Jf6in the functional of Eq.(5).The use of Jf1，Jf2，...，Jf6is sufficient to derive the reconstruction relation Eq.(8)for CVi.Therefore,the numerical methods in Section 2 can be readily extended to the AMR framework based on the compact stencil involving only the face-neighboring cells.

Remark 3.The compactness of the VR is essential for the present numerical methods to be applied in the p4est.In the parallel partition of the p4est algorithms,some ghost cells must be included in the partition to handle the data communication between different partitions.The p4est can only deal with one layer of the ghost cells,28and therefore requires the reconstruction stencil to be compact.Traditional reconstruction methods such as the k-exact reconstruction and the Weighted Essentially Non-Oscillatory(WENO)schemes on unstructured grids are not possible to be incorporated in the p4est directly since their reconstruction stencils are not compact.

Remark 4.The matrices in Eq.(8)are geometric quantities.In static grids applications,they are only computed once and stored.This technique is also used in the AMR framework.An exception is that matrices associated with newly generated cells should be recomputed and stored.

Remark 5.The p4est can only be applied to two-dimensional quadrilateral and three-dimensional hexahedral cells since the algorithms of searching,ordering,and load balancing developed in the p4est can only be used with octree data structures.However,the baseline mesh can be arbitrarily unstructured,which makes the present method being capable of handling rather complicated geometries.

Fig.7 Local grid after applying the AMR procedure.

Remark 6.In the present paper,grid refinement and coarsening operations are applied to high-order grids.In these operations,the surface grids are decomposed or composed without changing their original shapes which are provided in the baseline meshes generated by a high-order grid generator.35Therefore,during the grid refinement and coarsening operations,the grids are also shape-preserving.

The criteria for mesh refinement and coarsening are important elements of AMR approaches,which have been studied extensively.The criteria based on truncation errors25adjoint approaches26,27can be problem-independent,but mainly confined to mesh adaptation in steady flow simulations.In the present paper,we are more interested in the simulation of unsteady flows.In this case,criteria based on the identification of flow structures are more straightforward.In the present paper,three criteria are considered.

The first one is the shock indicator given by

which is used to identify shock waves.In Eq.(10),hi=is the length scale of the cell.is larger near shock waves.The second one is the entropy generation indicator defined by

which is to identify structures with large entropy generation.Entropy generation may be due to an existence of shock waves or a large numerical diffusion.The third one is a vortex indicator proposed in Ref.38as

and Sijand Qijare respectively the symmetric and antisymmetric parts of the velocity gradient tensor.

The grid adaptation strategy in the AMR approach of the present paper is as follows.Denoting Eias one of the criteria presented above in Eqs.(10)–(12),we compute its volume weighted average as

Furthermore,two user-defined positive parameters α1and α2are given with α1≥ α2.If Ei＞ α1Em,the corresponding control volume CViis refined.If Ei＜ α2Em,the corresponding control volume is flagged to be coarsened.If all leaf control volumes belonging to the same parent node in the octree are flagged to be coarsened,these leaves are deleted,and their parent control volume becomes a new leaf in the octree.This operation results in a combination of the leaf control volumes into a larger control volume which is originally the parent node of the deleted leaf control volumes.

4.Numerical results

In this section,several numerical test cases are solved to verify the accuracy and resolution of the proposed numerical schemes.The code based on the present numerical schemes is three-dimensional,but can be run in a two-dimensional mode.The first test case is a two-dimensional viscous shock tube problem to test the resolution of the present method in capturing shock waves and viscous vorticial structures.Third-and fourth-order FV schemes based on the VR are used to solve this problem without using AMR.In all other test cases,the code is run in a three-dimensional mode,and the AMR is applied.For all the AMR test cases,the numerical scheme is the fourth-order FV scheme based on the VR.

4.1.Two-dimensional viscous shock tube

This case39is characterized by interactions between strong shock waves,boundary layer,and vortex.The computational domain is a squared shock tube with adiabatic walls.Initially,a shock wave is located at x=0.5.The initial conditions are

where ρ,u,v and p are respectively the density,x component of velocity vector,y component of velocity vector,and pressure.

The Reynolds number is 200.The shock wave and a contact discontinuity move rightward and are reflected at the wall.A thin boundary layer is created by the interactions of the viscous wall with the shock wave and the contact discontinuity during their propagation.Complex flow structures are then produced by these interactions.In the present simulation,the grids are uniform square meshes with the length being h=1/353.Third-and fourth-order FV schemes using VR reconstruction are applied to solve this test case,and the density contours at t=1.0 are shown in Fig.8.Both schemes predict the shock waves in a high resolution.In Ref.30,the height of the primary vortex is used to measure the grid convergence of the simulation.In Table 1,it indicates that the height of the primary vortex predicted by the fourth-order scheme is much closer to the reference value than that by the third-order scheme.The reference value of the present paper is computed by solving the same problem using the fourth-order scheme on a finer grid.This result shows that the fourth-order scheme used in the present paper can compute the vortex structures in a higher resolution.

4.2.Lax shock tube problem

The initial condition of the Lax shock tube problem is

This is a one-dimensional problem governed by the Euler equations,which is solved using the proposed fourth-order three-dimensional AMR solver.The spatial computational domain is[ 0，1]× [0，0.2]× [0，0.2],and the baseline grid is uniform with a grid size of h=1/100.The depth of the octree is lmax=2,which means that the initial grids are at most subdivided twice in the AMR approach.The shock detectordefined in Eq.(10)is used as the grid refinement and coarsening criterion.The grids after the adaptation at t=0.2 are shown in Fig.9,and the density distributions are depicted in Fig.10.Compared with the results on the baseline mesh,the AMR results can predict shock as well as contact waves more sharply.To further study the efficiency of the AMR approach,the Efficiency Improvement Factor(EIF)is defined as Fei=Nm/N,where Nmis the grid number if all baseline meshes are subdivided recursively to the depth limit of the octree,and N is the actual grid number during the AMR procedure.In this test case,at t=0.2,the EIF is Fei=6.25,which means that 6.25 times of the current AMR grid number are needed if a uniform refinement is applied.

4.3.Supersonic flow about a cylinder

Fig.8 Density contours of the viscous shock tube problem.

Table 1 Height of the primary vortex.

Fig.9 AMR grids at t=0.2.

Fig.10 Density distributions at t=0.2.

In this test case,the Mach number 2 supersonic flow past a cylinder is solved.The initial grid is 5×15×12 in span-wise,radial,and circumferential directions respectively.The depth of the octree is 4.The entropy generation indicator Ei2defined in Eq.(11)is used as the grid refinement and coarsening criterion.Because this test case is a steady- flow problem,grid adaptation does not need to be implemented at each time step.Instead,grid adaptation is carried out four times during the computation.Fig.11(a)is the baseline grid,and Fig.11(b)is the grid after four times of adaptation.Fig.12 shows the pressure contours predicted based on the baseline grid and the adapted grid.The results indicate that by applying AMR,the shock wave can be captured in a much higher resolution.In this case,the EIF is Fei=240,which means that 240 times of the cells are needed if a uniform refinement to the depth limit of the octree is applied.Therefore,the use of the AMR can significantly improve the efficiency of the simulation for cases of inviscid flows with shock waves.

4.4.Low-speed viscous flow past a sphere

Fig.11 Baseline grid and the grid after AMR.

Fig.12 Pressure contours predicted on the baseline grid and the grid after AMR.

This test case is used to test the capability of the proposed method solving viscous flows.The free stream Mach number is 0.2535,and the Reynolds number based on the diameter of the sphere is 118.These parameters are chosen so that the drag coefficient is 1.0.40Grid adaptation is performed twice for this steady- flow case,and the depth of the octree is 2.The vortex indicator Ei3defined in Eq.(12)is used as the grid refinement and coarsening criterion.The initial grid and the corresponding flow field manifested by the streamlines are shown in Fig.13.Fig.14 shows the grids and the streamlines after the first adaptation.Comparing with Fig.13,we find that the grids near the sphere surface are refined,and the leeward separation region is elongated.After the second grid adaptation,the grids near the solid wall are further refined.On the other hand,the changes of the streamlines are very small as shown in Fig.15,which indicates that the grid density is sufficient to compute this test case.

In Table 2,some quantitative results are shown.Initially,there are 32768 cells in the computational domain.They are increased to 621440 after adaptation twice.The corresponding EIF is 3.4,which indicates that for a low-Reynolds number flow,the reduction of the cells due to AMR is not significant,since the flow is rather smooth everywhere without boundary layers.According to Table 2,the drag coefficient becomes closer to the reference value of 1.0 during the AMR process.

4.5.Viscous flow past an SD7003 wing

Fig.13 Baseline grids and corresponding streamlines.

Fig.14 Grids after the first adaptation and corresponding streamlines.

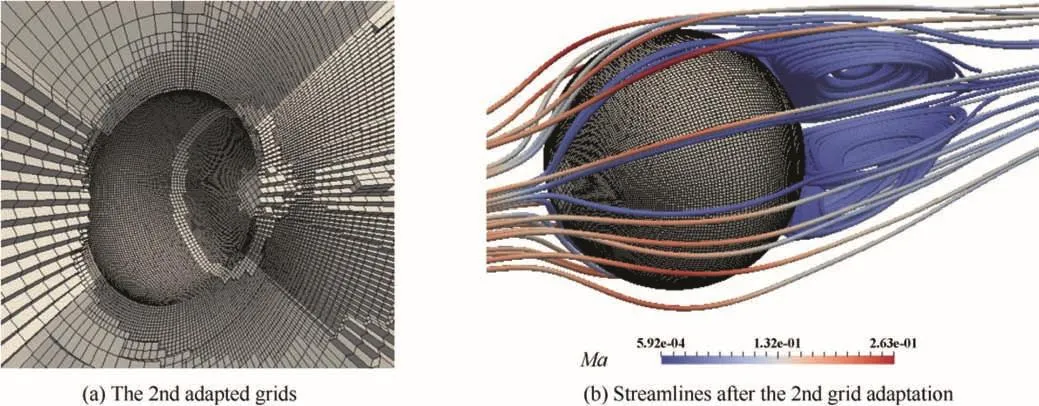
Fig.15 Grids after the second adaptation and corresponding streamlines.

Table 2 Quantitative results for flow past a sphere.

This test case is used to test the capability of the proposed numerical methods in solving transitional flows.The transition to turbulence is a very important phenomenon.The transition can be induced by the growth of disturbance and flow separation,which are in most cases limited to small regions.Therefore,the use of the AMR technique can improve the efficiency of simulation.In the present case of the flow past an SD7003 wing,the freestream Mach number is 0.2,the Reynolds number based on the chord of the wing is 6×104,and the angle of attack is 4°.The vortex indicatordefined in Eq.(12)is used as the grid refinement and coarsening criterion.The depth of the octree is 3,which means that the initial grids are at most subdivided three times in the AMR approach.The two-dimensional view of the baseline and final grids are shown in Fig.16.The initial grids have 41000 hexahedral cells,and during grid adaptation,the number of cells changes over time,since the flow is unsteady.When the flow reaches statistically steady states,the number of cells is around 1680000 which corresponds to an EIF Fei=12.5.Therefore,for the transitional flow with a relatively high Reynolds number,the reduction of the number of cells is quite significant.If a uniform refinement to the depth limit of the octree is applied,12.5 times of the current control volumes are required.

Fig.16 Two-dimensional view of the baseline and final grids.

Fig.17 Contour surface of Ei3.

Fig.18 Distributions of the pressure and skin friction coefficients.

Table 3 Comparison of the separation/transition/reattachment points between different results.

5.Conclusions

In the present paper,high-order FV schemes based on the VR are extended to solve three-dimensional inviscid and viscous flows on unstructured grids.To reduce the local condition number and to improve the robustness of the reconstruction algorithm on low-quality grids,a new cost function is proposed.To improve the efficiency of computation,the highorder FV schemes are incorporated with the AMR technique based on forest-of-octree data structures.The open-source library p4est is adopted to handle mesh connectivity and dynamic balancing during the AMR process.This is for the first time that the p4est AMR framework is used together with high-order FV schemes in terms of a compact stencil.Grid refinement and coarsening criteria based on the shock detector,entropy generation indicator,and vortex indicator are developed and tested.Numerical results show that the present numerical schemes predict flow fields in a high resolution.The AMR technique can improve the efficiency of computation considerably.In terms of the EIF,3.4 to 240 times of enhancements in the grid usage efficiency are achieved.

Acknowledgements

This work was supported by the National Natural Science Foundation of China(Nos.91752114 and 11672160).The AMR framework is based on the p4est library.