Pressure distribution guided supercritical wing optimization

Runze LI,Kaiwen DENG,Yufei ZHANG,Haixin CHEN

School of Aerospace Engineering,Tsinghua University,Beijing 100084,China

KEYWORDS Aerodynamic optimization;Man-in-loop;Pressure distribution;RBF-assisted;Supercritical wing

Abstract Pressure distribution is important information for engineers during an aerodynamic design process.Pressure Distribution Oriented(PDO)optimization design has been proposed to introduce pressure distribution manipulation into traditional performance dominated optimization.In previous PDO approaches,constraints or manual manipulation have been used to obtain a desirable pressure distribution.In the present paper,a new Pressure Distribution Guided(PDG)method is developed to enable better pressure distribution manipulation while maintaining optimization efficiency.Based on the RBF-Assisted Differential Evolution(RADE)algorithm,a surrogate model is built for target pressure distribution features.By introducing individuals suggested by suboptimization on the surrogate model into the population,the direction of optimal searching can be guided.Pressure distribution expectation and aerodynamic performance improvement can be achieved at the same time.The improvements of the PDG method are illustrated by comparing its design results and efficiency on airfoil optimization test cases with those obtained using other methods.Then the PDG method is applied on a dual-aisle airplane’s inner-board wing design.A total drag reduction of 8 drag counts is achieved.

1.Introduction

Optimization design is more and more widely used to gain practical industrial designs in recent years.Multiple types of optimization algorithms have been well developed for more efficient and capable industrial optimal searching.However,although there have been many efforts using optimization algorithms to improve aerodynamic performances,practical design via optimization is still limited,and ‘‘cut-&-try” is still heavily relied on in the aircraft industry.1On one hand,even though multi-objective and multi-constraint optimization has become popular,2,3the complexity of industrial considerations makes it difficult to define all engineering-needed objectives and constraints for optimization algorithms.4,5On the other hand,engineers find their experiences,considerations,and judgments difficult to be introduced into an automatic optimization design process.1,4,6–8Therefore,in order to gain an engineering-acceptable design,optimization design not only needs a robust and flexible algorithm to endure a large amount of objectives and constraints,but also needs ways to transfer those in-brain requirements into what the optimization algorithm can accept or process.

Experienced supercritical wing designers usually do not seek a wing with the highest lift/drag ratio,but a design that best compromises the performances of different disciplines and different flight conditions.What’s more,they emphasize much on design robustness,such as the drag divergence Mach number,the buffet onset lift coefficient,etc.Since both the performance and robustness are essentially the outcomes of flow structures as well as their evolutions,the flow physics is relatively clear.Engineers tend to judge a design through flow patterns and details.Currently,pressure distribution is the most cared flow structure in supercritical wing design.Many rules or criteria on pressure distribution have been proposed.For instance,the shock should be properly located to get a good robustness,and the aft loading of an airfoil should not be too large or else the nose-down pitching moment could be unacceptable.9–11

By realizing these explicit rules of hint experiences on pressure distribution,a designer could improve a wing’s design point performances while achieving preferable off-design and multi-disciplinary properties.This is basically what they do in ‘‘cut-&-try”.From the 1980s,with the development of inverse design methods12–14researchers tried to gain a design by realizing a desired pressure distribution.However,due to the difficulties of ‘‘designing” a physically-existing pressure distribution,even for a simple geometry at a specific flow condition,11,15the application of these methods in the industry is still limited.

Zhang et al.16studied the drag,moment,and especially robustness of three categories of typical pressure distributions for supercritical airfoils,i.e.,shock-free,double shock,and weak shock.The weak shock pressure distribution was evaluated as the best.Furthermore,other suggestions on pressure distribution have been proposed,such as that the shock location should range from 45%to 55%chord length for a single-aisle civil aircraft,the aft-loading should compromise the lift generation and a mild pitching moment,etc.To realize these suggestions,methods were developed to induce the pressure distribution to approach a desired pattern during optimization design.Some of them have been proven effective in industrial design.Optimal searching is no longer driven only by performances,but also by pressure distributions.Such methods are generalized in the present paper as Pressure Distribution Oriented(PDO)optimizations.

The PDO method has also been applied to a dual-aisle airplane wing design.17The cruise performance and robustness were improved while the proposed weak shock pressure distribution was also achieved.The shock location was pushed slightly downstream that of a single-aisle civil aircraft to fit a higher Reynolds number and different cruise lift coefficients.Both the single-and dual-aisle design studies have shown that the location of shock wave is a critical factor for a supercritical wing’s balance of performance and robustness.

Since the PDO method is characterized by the ability of manipulating pressure distributions,it can be consequently used to study the performance of a specified type of pressure distribution.By using the PDO method,Zhang et al.18achieved supercritical natural laminar airfoils with different pressure distributions characterized by assigned favorable pressure gradients and shock locations.Their gains on laminar friction reduction and penalties on the wave drag and robustness were then systematically compared.

There are two types of PDO optimization developed in previous studies according to their methods of manipulating pressure distributions.The first one can be called Pressure Distribution Constrained(PDC)method.16–18Constraints are set to rule out or punish designs with an unsatisfying pressure distributions shape.It essentially posts restrictions on the optimal search direction.The optimization efficiency and global optimal searching capability are inevitably deteriorated.

The other method is a manual or ‘‘man-in-loop”1,16one.Engineers can guide an optimization’s pressure distribution trend by manipulating the population.They need to introduce external individuals,which have the expected pressure distribution characteristics,into the population,or they need to eliminate unsatisfactory individuals from the population.This method demands a large amount of human labors and experiences.

In this paper,a new approach of using the pressure distribution expectation to guide optimization is developed.Instead of manual population control,the so-called Pressure Distribution Guided(PDG)method uses a surrogate model to search potential individuals which best satisfy the expectation on pressure distribution and also have excellent performances.These individuals are introduced into the population of an evolutionary optimization algorithm.In this way,the optimization process is automatically guided to approach the expected pressure distribution feature,while the diversity of the population during the optimization is well preserved.To more rationally define the ‘‘expectation” on the pressure distribution,several physical or empirical relations are also studied.

Unlike the PDC method,the pressure distribution is pursued by ‘‘guidance from good individuals” instead of ‘‘punishing bad individuals”.

As a new branch of PDO optimization,in the present paper,the idea of the PDG method is firstly introduced.It is then tested and compared with previous methods by airfoil cases.Proven by results that it has better optimal searching efficiency and pressure distribution manipulation capabilities,the PDG method is applied to the supercritical wing design of a dual-aisle civil airplane.

2.Optimization and modeling methods

2.1.RBF assisted differential evolution algorithm

An evolutionary optimization algorithm can use the assistance of surrogate models to improve efficiency.19In the present study,an RBF(radial basis function)Assisted Differential Evolution(RADE)algorithm is used as the primary optimization algorithm.20The basic flow chart of the RADE algorithm is outlined in Fig.1(a),in which k is the index of the current generation and P is short for population.The dash box contains the main optimization process of Differential Evolution(DE)optimization,and the upper part outside the box shows the RBF surrogate model’s behavior.By utilizing computed individuals’information,the RBF surrogate model can obtain approximation of CFD results.Then an optimal search is conducted on the RBF response surface to find individuals that are most likely to produce excellent objectives.Those individuals are added into the current candidate population to participate in the main DE optimization process.Since the search direction of an evolutionary algorithm is mainly based on the candidate population and the sorting strategy,this will form guidance to the search direction.In RADE,the surrogate model is not a substitution to an accurate CFD analysis.For individuals from both the main DE optimization process and the RBF surrogate model,a CFD objective evaluation is fully conducted.

Fig.1 Flow charts of the RADE algorithm and PDC method and the PDG method.

In an original RADE algorithm,the optimal search on the RBF surrogate model shares the same objectives and constraints as those of the main DE process.The purpose of the surrogate model is only to accelerate the main optimization process.The whole method can be used as a black-box multi-objective multi-constraints optimizer.The PDC and man-in-loop pressure distribution manipulation can both be directly realized on the RADE.The optimization can be directed to achieve the expected pressure distribution through manually adding/eliminating individuals by people,or through automatically eliminating individuals by constraints on the pressure distribution shape.

There are drawbacks in these methods.For manual population manipulation,the basic idea is to manually judge all calculated individuals’pressure distributions and add or delete individuals to reconstruct the current population for evolutionary operators.On the contrary,the constraints of PDC optimization limit the optimization direction by eliminating non-feasible individuals,and then the population will meet the constraints eventually.Both methods alter the candidate population according to an engineer’s judgment,for example,their consideration on pressure distribution.However,eliminated individuals might have good objective function values,while artificially-introduced individuals usually do not have good enough performances to survive in the sorting procedure.Therefore,the optimization efficiency often suffers badly.If the introduced individuals could have competitive performances,the efficiency should be able to be maintained.

Furthermore,proposed pressure distribution features may compromise the performance and robustness,and hence the method should only provide attempts on these features instead of forcing the entire population achieving them.

The present PDG method is based on a modification to the RADE algorithm.The surrogate model contains the mapping between pressure distribution characteristic parameters and the design variable space.Objectives and constraints can be set different from those of the main DE process.A multiobjective optimal search on the RBF surrogate model is constructed to find potential individuals that have both good performances and expected pressure distribution features.These potential individuals are introduced to the DE’s candidate population to guide the optimization process,instead of forcing the entire population like the PDC method does.The constraints on the pressure distribution in the DE can therefore be relaxed or eliminated in the PDG process.The realization of the PDG method is shown in Fig.1(b).

2.2.Modeling and numerical method

The Class Shape Transformation(CST)method is widely used in wing design due to its capability of constructing a smooth airfoil with a few design variables.18In the present paper,a 6th-order Bernstein polynomial is used as the shape function for both the upper and lower surfaces of an airfoil.The number of design variables for an airfoil is 14.The ranges of the variables are the same as those in Ref.18.The wing surface is constructed by interpolation with several span-wise distributed airfoils.

The aerodynamic performances of airfoils and wings are evaluated by an in-house solver,21,22which is a cell-centered finite volume compressible Reynolds Average Navier-Stokes(RANS)solver with multiple types of numerical schemes and turbulence models.The solver has been validated by various test cases and successfully applied in many industrial design activities.16–18,21–23In this paper,it employs the MUSCL scheme for the reconstruction,Roe’s scheme for the spatial discretization,the lower-upper symmetric Gauss-Seidel method for the time advancing,and the Shear Stress Transport(SST)model for the turbulence modeling.The accuracy of the solver has been validated by our previous study.23

3.Method validation

3.1.Pressure distribution consideration of a supercritical wing

For a supercritical wing,the pressure distribution contains various information of aerodynamic characteristics.Since the off design performances are essentially the outcome of the flow structure evolution among different flight conditions,it is not necessary to evaluate the drag divergence Mach number or buffet onset point through CFD calculations of a series of flight conditions.Pressure distribution manipulation and performance optimization on several typical conditions can suffice.1,17

On the other hand,many important characteristics are directly associated with certain flow patterns,such as the wave drag and the shockwave strength.Some experience of pressure distribution has been gathered to gain a fine compromise among lift,drag,moment,shockwave stability,trailing edge separation characteristic,and geometry considerations.16However,features are different for different flight conditions and different aircraft planforms.A dual-aisle aircraft usually has a higher flight Mach number and a higher Reynolds number than those of a single-aisle aircraft,and the shockwave is downstream with a higher strength.Therefore,the wave drag is a major party in drag reduction,and the off-design characteristic is more non-linear.In this paper,several pressure distribution considerations16of a wing of a dual-aisle aircraft at a flight Mach number of 0.85 are taken in the following optimizations.The pressure distribution considerations of an airfoil are transformed according to the cosine rule of a swept wing.23These considerations can be expressed as follows:

(1)The pressure coefficient of the suction peak of a wing cannot be lower than-1.0;otherwise,the flow accelerates too much around the leading edge,which will make the aerodynamic performance like that of ‘‘peaky”airfoils.24

(2)The slope of the pressure plateau on the upper surface(from the suction peak to the shockwave front)shall be between-0.2 and 0.5 to ensure an appropriate length of the suction platform for providing enough lift.

(3)The pressure plateau shall be as smooth as possible to avoid undesirable robustness issues.

(4)The slope of the pressure recovery zone near the trailing edge of a wing is kept lower than 3.0 to prevent flow separation.

(5)The aft loading shall not be too large,or else the nosedown pitching moment will be too large.

3.2.Relation between shockwave strength and drag coefficient

The wave drag is directly related to the shockwave strength.Although the shockwave strength may have different definitions in previous studies,it can be roughly described by the pressure rise between the two sides of the shockwave ΔCp,as shown in Fig.2.According to the Oswatitsch theorem,25the wave drag of an airfoil can be described as in Eq.(1)under the assumption of isentropic flow before the shockwave,where Ma1is the Mach number at the wave front.

The pressure coefficient can be defined aswhere γ is the specific heat ratio,Ma∞is the freestream Mach number,and p/p∞is the ratio of static pressure normalized by the freestream value.Then ΔCpcan be described as in Eq.(2)using the isentropic relation and the Rankine-Hugoniot equation.

Fig.2 Definitions of Err and ΔCp.

Then the wave drag can be expressed as in Eq.(3),where S is a coefficient associated with the airfoil shape and the flight condition.

A large number of supercritical airfoils through optimization are gathered to verify the relation.The airfoils are evaluated by RANS.The free stream Mach number is 0.742,and the Reynolds number is 10 million.The lift coefficients of the airfoils are kept the same(CL=0.787).The airfoils all have similar flow patterns,which are a single shockwave and a smooth suction plateau,and all airfoils have normalized chord length,i.e.X ∈ [0，1].The smoothness function Err is defined as Cpfluctuations on the suction plateau,which is the area of the blue shadow region in Fig.2.The pressure distribution in Fig.2 has a smoothness function of Err=0.012.The drag coefficients of the sampled airfoils which have small fluctuations(Err＜0.012)are shown in Fig.3.A curve fitting relation between the drag coefficient CDand the shockwave strength ΔCpis shown as the red curve in Fig.3,where the coefficient S equals to 0.05,and CD0is the smallest drag coefficient for non-shockwave airfoils.

Fig.3 Relation between total drag and shockwave strength.

The sampled airfoils fit the curve with a less than 0.1 derivation of ΔCp.Therefore,the shockwave strength is correlated with the total drag and can be used as an effective auxiliary parameter for drag reduction.It is also a parameter to distinguish between different pressure distribution types.As shown in Fig.3,when ΔCpis less than 0.3,the drag coefficient penalty caused by the shock wave is smaller than 0.0005,and the drag reduction caused by shockwave weakening is negligible when ΔCpis less than 0.2.Moreover,it demonstrates that airfoils with the same total drag coefficient can have different shockwave strengths,which reveals that while keeping the total drag unchanged,the shock strength can be adjusted to get a better robustness.Therefore,if the shockwave strength is used as an objective or sub-objective in a drag reduction optimization,it could have the potential to increase the overall optimization efficiency or robustness.

3.3.Single-objective PDG optimization

Pressure distribution features can be used as objectives in the main optimization process,or in the sub-optimization process.In this section,single-objective optimizations of a supercritical airfoil with different optimization settings are compared to demonstrate the acceleration effect of sub-optimization.The free stream Mach number is 0.742,the Reynolds number is 10 million,and the lift coefficient is kept 0.787 during the optimization.The design variables are 14 CST parameters.

Five settings are studied in this case,as shown in Table 1,where RLEis the airfoil leading edge radius.Opt1 and Opt2 are baseline PDC optimizations using DE and RADE algorithms,respectively.Opt3 and Opt4 directly use the shockwave strength as an overall objective of RADE.Opt1 has no suboptimization process.Opt2,Opt3,and Opt4 have the same objectives and constraints in both the main optimization process and the sub-optimization;therefore,Opt3 and Opt4 are still called PDC optimizations.Opt5 uses the modified RADE with different objectives and constraints in the main optimization process and the sub-optimization,which is a demonstration of the present PDG method.According to the relation between the shockwave strength and the drag coefficient in Section 3.2,ΔCpis used as a sub-objective to guide the optimization generating airfoil designs for an inboard wing,of which ΔCpis expected to be smaller than 0.2.Pressure distribution considerations described in Section 3.1 are also applied as constraints in the main optimization.

The population sizes of all the cases are 32,and 32 generations are carried out to compare the efficiency and effectiveness.All the cases have the same initial population,and the averaged drag coefficients of the final generation are used for comparison,as shown in Table 2.The convergence histories are shown in Fig.4.Table 2 shows that Opt2 has a slightly better final result than that of Opt1,and a result that has a similar performance to the final result of Opt1 can be achieved by Opt2 with only around 600 individuals,as shown in Fig.4,where ID is the index of each individual.Therefore,the RBF-assisted method could improve the efficiency of the optimization.

Table 1 Optimization settings of 5 cases.

Table 2 Final results of 5 cases.

Fig.4 Convergence histories of the five cases.

Fig.5 shows two typical pressure distributions of the results which have an unsatisfactory performance.The strong shockwave airfoil(Fig.5(a))whose CDequals to 0.01071 is the initial design.Although reducing the shockwave strength can reduce the wave drag,shock-free and weak-shock airfoils are not the only possibilities for reducing the shockwave.Due to a lack of proper constraints,Opt3 wastes part of its ability to search in a wrong direction,i.e.,airfoils with massive upper surface separation or double-shockwave airfoils(Fig.5(b)).Moreover,excessive constraints can have negative effects on the main process,as shown in Opt4,and the overall efficiency is low.Opt5 uses the shockwave strength as a sub-objective to provide an alternative searching direction for the main process.Because the computation cost for searching on the RBF is negligible,the efficiency of the main optimization process is not depressed.Table 2 shows that Opt5 has the best final result in all of the five optimizations.Fig.4 shows that a result similar to the final result of Opt2 can be achieved by Opt5 with around 500 individuals.Therefore,the optimization is accelerated by the sub-optimization,and the desired pressure distribution feature is achieved.

Fig.6 shows the final result of Opt5,of which CDequals to 0.00958.The pressure distribution type is shock-free.The pressure distribution satisfies all of the constraints in the optimization,but the robustness is not good according to Ref.16.This case is only a demonstration of the PDG optimization.Multi-point optimization is carried out in the next section to improve the robustness.

Fig.5 Typical pressure distributions with an unsatisfied performance.

In summary,the PDG optimization is achieved by a combination of the main optimization process and sub-optimization.As shown by the results of Opt3 and Opt4,the pressure distribution features used as main process objectives might lead to undesired results,while adding more constraints in the main optimization process leads to a low efficiency.The PDG optimization,i.e.,Opt5,uses sub-objectives and sub-constraints to utilize the pressure distribution expectation,and the efficiency is not compromised.Moreover,the sub-optimization only serves as a source of potential individuals to the main process.Therefore,the sub-optimization can handleflexible expectations of engineers without interfering the entire optimization efficiency.

3.4.Multi-point pressure distribution guided optimization

Different methods of pressure distribution oriented optimization along with a baseline optimization are compared in this section.Cases are used to demonstrate the PDG method’s effectiveness of pressure distribution manipulation and optimization.A multi-point airfoil optimization is applied based on the RADE algorithm.The airfoil is expected to have a shockwave location at 50%chord length at the cruise condition.This case is to demonstrate the pressure distribution control ability of the present method.In order to make the comparison simple and clear,only the cruise drag(CD0)is used as the objective of the main optimization process.Drag divergence and buffet onset control are maintained through constraints.Flight conditions are shown in Table 3.The objectives and constraints of 4 different settings can be seen in Table 4.

Fig.6 Pressure distribution of Opt5’s final result.

Table 3 Flight conditions of three design points.

Opt1 is the baseline optimization.Opt2 is a demonstration of manual population manipulation.Since the final effect can be highly influenced by different engineers’involvement,a fixed strategy is programed into the optimization sorting strategy to mimic the manual manipulation.The basic idea of manual manipulation is to select individuals for the DE operators based on personal judgement of performance and pressure distribution considerations.In this case,individuals with a low drag and a single shockwave in all 3 flight conditions as well as a small value of| XSW0-0.5|are more likely to be selected.The strategy for Opt2 is shown in Fig.7.Opt3 applies constraints of the shockwave position| XSW0-0.5|＜0.05.Opt1,Opt2,and Opt3 share the same objectives and constraints in the main optimization process and the sub-optimization.Opt4 uses the PDG method,which means more objectives and constraints are applied in the sub-optimization to guide the search direction of the optimization.According to the relation between the shockwave strength and the drag coefficient in Section 3.2,the shockwave strength at the cruise condition is constrained by ΔCp0＜ 0.3 in the sub-optimization.

Fig.8 shows the convergence histories of the optimizations.Fig.8(a)is the objective of the cruise condition.Fig.8(b)is the pressure distribution consideration,i.e.,the distance between the shockwave and the half chord length.Fig.8(c)and(d)show the drag increments for the drag divergence condition and the buffet onset point.The dash lines in Fig.8(b)–(d)show the critical constraint values.Table 5 shows some statistical results of the methods.Fig.9(a)shows the individuals within the requested shock wave region,i.e.,45–55%,and only the ones meeting all the constraints are included.A typical optimized result is shown in Fig.9(b).It is a weakshockwave airfoil with a cruise drag of 0.00988.

As shown by the results in Fig.8(b),compared to Opt1,all the pressure distribution oriented methods are able to get shockwaves in the requested region.The results of Opt1 are almost equally distributed in different shock locations.By contrast,the results of Opt2 to Opt4 are getting near 50%chord length when the optimization proceeds.Table 5 shows that Opt2 and Opt3 have fewer results satisfying Opt1 constraints than those of Opt1,whereas Opt2 and Opt3 have more results satisfying Opt3 constraints.Therefore,although manual population manipulation and constraints in Opt3 and Opt4 have a better efficiency generating results with shockwaves in the requested region,the ability of generating results satisfying basic constraints,i.e.,Opt1 constraints,is compromised.By contrast,Opt4 has more results satisfying Opt1 and Opt3 constraints,and these results have shockwaves near the required 50%chord length location.

According to the results of Opt2 and Opt3,we can see that the constraint in the main optimization process is more objective than manual manipulation,but also more in flexible.When the critical value for| XSW0-0.5|constraint is small,the constraint may eliminate most individuals in the early stage of the optimization,and a convergence is hard to achieve.However,if a loose constraint is applied,the final results cannot satisfy the expectation of the shockwave location.

Opt4 applies more objectives and constraints in the sub-optimization to guide the searching direction.Thesub-optimization provides promising individuals for the main process.Since the sub-constraints are stronger and the shockwave strength along with| XSW0-0.5|are also used as subobjectives,the individuals provided by the sub-optimization have a higher possibility to reduce the drag and meet the constraints synchronously.Moreover,because the drag divergence and buffet characteristics are associated with shockwave induced boundary layer separation,the sub-constraints about the shockwave strength in these flight conditions can help improving the robustness,and then accelerating the main optimization process.Therefore,the PDG method could increase the optimization efficiency and generate more desirable results.

Table 4 Four different optimization settings.

Fig.7 Flow chart with an additional sorting strategy for Opt2.

Table 5 Statistics of the 4 optimization settings.

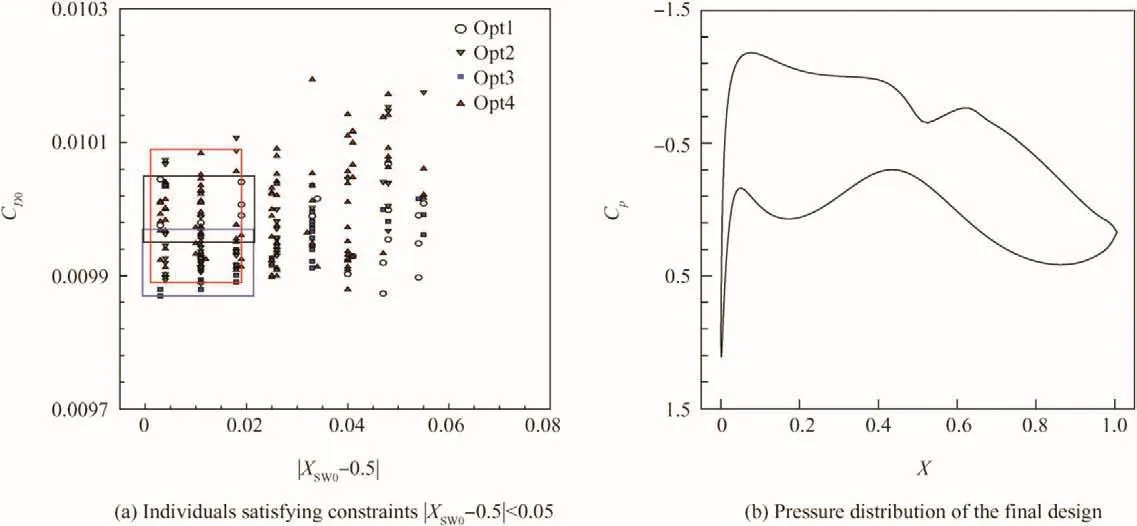
Fig.9 Final results of the 4 optimization settings.

4.Method application

Previous studies16,17have indicated that a weak-shockwave pressure distribution has a better balance between the cruise performance and the robustness than those of doubleshockwave and shock-free pressure distributions on a singleaisle airplane.However,since a dual-aisle airplane has a different planform and a different flight condition,the details of preferable features are unclear,especially for the inboard wing.The inboard wing has a much longer chord length than that of the outboard wing,and hence a small modification of the inboard wing can have a significant impact on the span-wise load distribution and a strong influence on the wing performance.Meanwhile,the inboard wing’s pressure distribution can directly influence the outboard wing due to the cross flow,and the interference of the wing,fuselage,and nacelle/pylon makes the non-linear phenomenon even more severe than on a single-aisle airplane.As from the discussion of the CD- ΔCprelation in Section 3.2,once ΔCpfor an airfoil is lower than 0.3,the drag increment caused by a shockwave is insignificant.Therefore,a weak shockwave of ΔCp=0.3 can be a good balance between cruise drag and robustness.

For a typical supercritical airfoil,once the shockwave strength ΔCpis fixed,the section lift coefficient is mainly dependent on the suction plateau and the shockwave location.A higher suction peak causes a strong pressure recovery on the suction plateau,and may induce unsatisfying robustness.A further downstream shockwave location tends to have a slightly stronger pressure recovery behind the shockwave,which may increase the risk of shockwave-induced boundary layer separation,but it also provides more lift.It is especially important for the inboard wing,because an increment of the lift coefficient of inboard wing sections can lead to a large reduction of the outboard wing load,which is good for improving the buffet characteristics.Therefore,when the shockwave strength ΔCpis kept lower than 0.3,a further downstream shockwave location and a lower suction peak on the inboard wing may result in a more excellent lift/drag ratio and robustness.

A dual-aisle airplane is used as the test case for the inboard wing optimization based on the PDG method.The cruise Mach number is 0.85,the Reynolds number is 40 million,and the lift coefficient is 0.48.The baseline wing was designed in our previous study,23which mainly focused on the outboard wing optimization.The baseline wing has an excellent robustness and a satisfying weak-shockwave pressure distribution on the outboard part.However,there is a strong shock on the inboard wing.In this paper,it is used to study different inboard wing pressure distributions and the influence on the overall performances.The inboard wing geometry is interpolated by 3 airfoils generated by the CST method.The locations are shown as Sections 1–3 in Fig.10.The design variables are the 42 CST variables of the 3 airfoils,and the computational mesh is the same as that in our previous study.23The black solid and dash lines in Fig.10 show the shockwave location of the baseline wing and the expected inboard wing shockwave location,respectively.

Fig.10 Wing section locations and shockwave locations.

The PDG method is used to manipulate the pressure distribution while reducing the cruise drag.Optimization settings are listed in Table 6.The cruise drag is set as the main objective and sub-objective.The distance between the actual shockwave location and the proposed position as well as the shockwave strength are also adopted as sub-objectives.The pressure distribution considerations mentioned in Section 3.1 are used as constraints,as well as the constraints about the geometry and the shockwave strength.The optimization population in each generation has a size of 40 individuals,and total 25 generations are carried out to gain final results.The convergence history is shown in Fig.11(a).Results with and without proposed features are used to compare the performances.Four typical results in Fig.11(b)are selected to compare the performances and pressure distributions.The pressure distributions are shown in Fig.12.The characteristics of the pressure distributions are shown in Table 7.The average values in the table are based on the values of Sections 1–4 in Fig.10.

Design4 in Table 7 is the final result of the optimization.It has the minimum drag coefficient of all feasible results and a short distance to the proposed shock location.Although it has a weak double shock on the 17.5%half-span section,it does not violate the constraints of the main optimization pro-cess.Design3 is also a typical result for drag reduction.However,it cannot satisfy the constraint of the shockwave location,and its suction peak is high.Design2 shows that when the double shock in Design4 is eliminated,the drag reduction quantity is limited.If a lower suction peak is applied,i.e.,in Design1,the cruise drag is compromised.

Table 6 Settings of dual-aisle airplane inboard wing optimization.

Fig.11 Optimization history and results.

Fig.12 Wing section pressure distributions of typical results.

Table 7 Cruise performances of the baseline and typical results.

Fig.13 shows the shockwave locations and span-wise loads of the wings.Basically,a further downstream shockwave has a larger inboard wing load(Design4);consequently,the maximum lift coefficient on the outboard wing is reduced,which usually means a weak shockwave strength(see Fig.12,17.5%,32.7%,and 45.0%sections)and a potentially better buffet characteristic.

Fig.14(a)shows the Cmvs CLcurves of the 4 results.Fig.14(b)shows the CDvs Ma curve.Inflection in a Cmvs CLcurve can be used to define the buffet onset26.The CDvs Ma curve is used to determine the drag divergence Mach number.It can be seen that designs with a larger inboard wing load have a larger buffet onset lift coefficient.Although Design4 has a similar cruise drag and a similar drag divergence performance to those of Design3,it has a better buffet characteristic.Through the present optimization with the PDG method,the proposed shockwave location and the pressure distribution expectations of a dual-aisle airplane are achieved.The result shows that the optimized design has a low drag and good buffet and drag divergence performances.

Fig.14 Buffet and drag divergence characteristics.

5.Conclusions

The pressure distribution of a supercritical wing contains comprehensive information about its performance and robustness.Pressure distribution oriented optimization can help achieve more engineering-applicable designs.This paper has developed a pressure distribution guided method of PDO optimization to introduce the considerations of pressure distribution into the optimization process.The work of this paper can be summarized as follows:

(1)The PDG method is developed based on an RBF-assisted differential evolution algorithm.The suboptimization on the RBF response surface can have objectives and constraints different from those of the main optimization process.By generating candidate individuals more likely to have both satisfactory pressure distribution features and performances,the suboptimization enables the PDG method to better manipulate the pressure distribution while maintaining the aerodynamic optimization efficiency.

(2)The relation between the shockwave strength and the drag coefficient is theoretically and statistically discussed in this paper.The result shows that the shockwave influence on the drag coefficient is insignificant when the shockwave strength is lower than 0.3.

(3)Single-and multi-point optimizations of supercritical airfoils are carried out to study the efficiency of the PDG method.The results show that setting the shockwave strength as the objective for the sub-optimization can accelerate the drag optimization process,and the PDG method is able to more effectively achieve the pressure distribution expectation.

(4)The PDG method is applied on the inboard wing design of a dual-aisle airplane.A proposed shockwave location of the inboard wing is achieved through different pressure distribution manipulation methods.The performance and robustness of the final result and some other typical results are compared.The results show that the PDG method can gain designs with the proposed pressure distribution while maintaining the aerodynamic optimization efficiency.The results also show that a weak-shockwave pressure distribution is a satisfactory balance between cruise drag and robustness.

Acknowledgements

This work was co-supported by the National Key Basic Research Program of China(No.2014CB744806)and Tsinghua University Initiative Scientific Research Program(No.2015Z22003).