A high- fidelity design methodology using LES-based simulation and POD-based emulation:A case study of swirl injectors

Xingjian WANG,Shiang-Ting YEH,Yu-Hung CHANG,Vigor YANG

School of Aerospace Engineering,Georgia Institute of Technology,Atlanta GA 30332,USA

KEYWORDS Emulation;High- fidelity design;Kriging;Large Eddy Simulation(LES);Proper Orthogonal Decomposition(POD);Swirl injector

Abstract Engineering design is undergoing a paradigm shift from design for performance to design for affordability,operability,and durability,seeking multi-objective optimization.To facilitate this transformation,significantly extended design freedom and knowledge must be available in the early design stages.This paper presents a high- fidelity framework for design and optimization of the liquid swirl injectors that are widely used in aerospace propulsion and power-generation systems.The framework assembles a set of techniques,including Design Of Experiment(DOE),high- fidelity Large Eddy Simulations(LES),machine learning,Proper Orthogonal Decomposition(POD)-based Kriging surrogate modeling(emulation),inverse problem optimization,and uncertainty quantification.LES-based simulations can reveal detailed spatiotemporal evolution of flow structures and flame dynamics in a high- fidelity manner,and identify important injector design parameters according to their effects on propellant mixing, flame stabilization,and thermal protection.For a given a space of design parameters,DOE determines the number of design points to perform LES-based simulations.POD-based emulations,trained by the LES database,can effectively explore the design space and deduce an optimal group of design parameters in a turn-around time that is reduced by three orders of magnitude.The accuracy of the emulated results is validated,and the uncertainty of prediction is quantified.The proposed design methodology is expected to profoundly extend the knowledge base and reduce the cost for initial design stages.

1.Introduction

Fig.1 Life-cycle design stages.1

Engineering design is undergoing a paradigm shift from design for performance to design for affordability,operability,and durability,seeking multi-objective optimization.There are typically four stages in a life-cycle engineering design:requirements definition,conceptual design,preliminary design,and detailed design as shown in Fig.1.1In the first stage,the requirements posed by the customer are defined.Conceptual design then starts based on experience and prior knowledge.Preliminary design involves transforming the concept so that the product can function properly and meet the customer/market demands.Further testing and fine-tuning is performed in the detailed-design stage.In today’s design methodologies,as a program reaches the preliminary design phase,the amount of design freedom rapidly decreases,while the cost commitment and need for design knowledge drastically increase.For the F-1 rocket engine development in the Apollo lunar landing project,for example,2more than 1300 component and engine tests were performed during the detailed-design stage to mitigate combustion instabilities,accumulating a tremendous design cost.To remedy this situation,an innovative design process is needed to bring more knowledge to the earlier design phase,keeping design freedom open longer and optimizing cost commitment,as depicted in Fig.1.

To facilitate the aforementioned design process,a more in depth analysis at the conceptual and preliminary stages is required.In addition,the design cycle time should be shortened along with the reduced cost.Multi-disciplinary design analysis and optimization needs to be incorporated in order to achieve those goals.A key enabler is high- fidelity physics based modeling and simulations,which plays a vital role for efficient design surveys.These models streamline trade-off analysis and concept selection during the early design.Formulating these models usually requires lower- fidelity,less expensive models to complement the primary,high- fidelity calculations to improve iteration turnaround times.This strategy is called multi- fidelity design optimization.3The use of secondary,correlated quantities to enhance model performance is not a new concept,as there is an established approach of model building using objectives resulting from computational simulations of varying fidelities and costs.4The methodology has been improved by combining flexible location and scale adjustments of the abundant,low- fidelity data to be closer to the high- fidelity data,using Bayesian hierarchical Gaussian process models.5

Much of early literature revolved around treating different mesh levels as an indicator of fidelity,6which evolved into treating the hierarchy of flow solvers as different fidelities.Global optimization(based on scalar metrics such as aerodynamic coefficients and wall conditions)using neural-network and polynomial-based response surface methodologies has been demonstrated for various applications,ranging from wing aerodynamics,turbulent diffuser flows,gas-gas injectors,and supersonic turbines.7Kriging,a Gaussian Process(GP)modeling,has been shown to perform better global approximations than response surface models,as it utilizes a ‘‘global” model and Gaussian correlation functions.8This model drastically reduces the computational time required for design space exploration and evaluating the objective function in the optimization process.9Kriging can also be employed to construct effective surrogate models to integrate information from both high- fidelity and low- fidelity models,while interpolation uncertainty of the model is quantified.10Techniques emphasizing reduction of high-dimensional design spaces,such as corrected space mapping for variable-parametrization design spaces11and imposing Partial Differential Equations(PDE)-constraints,12can further reduce computational costs.

Since the introduction of modeling deterministic outputs as a realization of a stochastic process and formulating a statistical basis for designing experiments,13statistical techniques have been used to build approximations(surrogate models)of expensive computer analysis codes to facilitate multidisciplinary,multi-objective optimization and concept exploration.14The conceptual and preliminary design of aerospace systems require tools that are capable of providing adequate fidelity and efficient evaluation for design space exploration.Aerodynamic performance has been the focal point for multi- fidelity design procedures,in which a conceptual low fidelity optimization tool is combined with a hierarchy of flow solvers of increasing fidelity.15,16Relying on interpolation error of radial basis functions between a high- fidelity and a low- fidelity function,maximum likelihood estimator models can be generated based on Kriging variance estimates,and have shown convergence and robustness with respect to low fidelity information in a trusted region.17There are typically three applications for multi- fidelity models:uncertainty propagation,statistical inference,and optimization.The construction of surrogate models can typically be split between simplified models,projection-based reduced models,and data- fit models.Simplified models are derived from high fidelity models,through simplifying physics assumptions or linearization.Projection-based models are computed by projecting the governing equations of a high- fidelity model onto a low-dimensional space.Data- fit models are formulated directly from the data,relying on black-box high- fidelity models and response surface approximations through regression analysis.

The data required for formulating a low- fidelity model can be severely limited by the time and computation constraints of high- fidelity simulations.Fig.2 shows the Pareto frontier for computational modeling and simulation capability.18In multi-objective optimization,when different objectives are conflicting,an optimal solution can be obtained accounting for the trade-offs.The set of all Pareto optimal solutions is called Pareto frontier.The figure illustrates the trade-off between the level of model fidelity and the extent to which the designer explores the design space.In some cases,this problem can be alleviated by performing a low- fidelity model and translating the result to a higher- fidelity model.In other instances, low- fidelity data, employing corrections for improved accuracy,can be combined with high- fidelity data to reduce the overall number of expensive runs.The current work is in the middle circle,having a broad scope of design and retaining the high- fidelity information required to analyze system dynamics.With continuing progress in modeling capabilities,simulation-based optimization has proven to be a useful tool in the design process,but complex design problems can still be a daunting task.

Fig.2 Pareto frontier of computational modeling and simulation capability.18

The present study proposes a novel design methodology that combines high- fidelity simulation and Proper Orthogonal Decomposition(POD)-based emulation to reduce the cost and time of the initial design stages.Unlike conventional surrogate models,the emulation framework maintains the high- fidelity information,capturing detailed spatiotemporal evolution of flow structures and dynamics.High- fidelity simulations are first used to explore the flow physics using Large Eddy Simulations(LES).The number of simulations is determined by Design Of Experiment(DOE).Results are then systematically analyzed using sensitivity analysis and machine learning to identify the key design parameters and classify the design points according to the output responses.Next,surrogate modeling(emulation)is performed through POD analysis and GP regression(Kriging),which is benchmarked against high- fidelity simulations.The overall framework can provide detailed physics,identify key design parameters,reconstruct a spatiotemporally evolving flow field,and predict output performance at a new design point in an efficient manner.Finally,a case study of supercritical- fluid swirl injectors is performed to demonstrate the effectiveness of the approach.

2.Methodology

Fig.3 shows the proposed design methodology.It begins,as in traditional methods,with a set of input parameters including various geometrical variations and operating limits.Then,DOE is used to obtain the optimal design parameter sets for training the surrogate model.For a given number of design variables,a practical number of simulation points are planned.During collection of training data,high- fidelity simulations are analyzed and physically interpreted.Important physical mechanisms are identified,and responses are extracted via post processing.The careful analysis of high- fidelity simulations can quantify the relationship between key flow physics and design parameters.This knowledge enables the use of sensitivity analysis for parameter reduction and supervised learning for data classification,facilitating the model training process.The surrogate model relies on the physical knowledge obtained from the simulations to properly retain high- fidelity information.

2.1.Design of experiment

In the early design stages of a complex system,the design space needs to be surveyed to identify the optimal range for design parameters and feasible starting points.An integrated design process combining design principles such as Taguchi methods and response surface methodology19into one mathematical framework can be used to address this multi-objective design concept problem.The critical component of the optimization problem is to properly identify the response function.

High- fidelity simulations take excessive run times,so optimization based on an inexpensive surrogate model is required.A surrogate model provides effective means to speed up computations,protect proprietary codes,and overcome organizational barriers.For problems involving spatiotemporal evolution,a surrogate model needs to be formulated such that the essential flow physics are captured.20Surrogate-based optimization can provide quantitative assessment of design tradeoffs and facilitate global sensitivity evaluations of design parameters.The surrogates constructed using data drawn from high- fidelity simulations provide efficient approximations of the objectives at new design points,rendering trade-off studies feasible.A sufficient number of different designs must be examined to build the surrogate model;the process of selecting different designs is DOE,a statistical methodology to determine the ideal training design points for surrogate modeling for a given design space.Two different DOE methods,Maximum Projection(MaxPro)21and Sliced Latin Hypercube Design(SLHD),22are considered in the present study.The former has good space- filling properties and GP modeling predictions,but it does not provide a sequential design capability,as the SLHD does.The design points for the SLHD are partitioned into slices of smaller Latin hypercube designs,rendering a design that is flexible as to size and parameters.The spacefilling performance of the design points in each slice is optimal.

2.2.LES-based high- fidelity simulations

2.2.1.Governing equations

Propulsion and power-generation systems often operate at pressures higher than the thermodynamic critical points of the propellants involved,commonly known as supercritical conditions.23Advances in fluid- flow modeling and simulation techniques over the past few decades have enabled highfidelity representation and improved understanding of intricate flow physics and combustion dynamics in the supercritical regime.Here ‘‘high- fidelity” refers to simulations that can capture turbulent flow dynamics over a wide range of length and time scales.In the present work,the LES technique is adopted to perform high- fidelity simulations at all design points.The formulation is based on Favre- filtered conservation equations24,25written as follows:

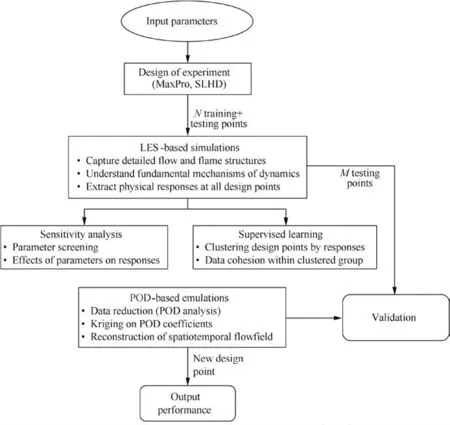
Fig.3 High- fidelity design methodology with LES-based simulation and POD-based emulation(N and M are number of design points).

Here overbars and tildes represent Reynolds and Favre averaging,respectively.ρ,uj,p,et,φ,τijand qjdenote density,velocity,pressure,total specific energy,scalar,viscous stress tensor,and heat flux,respectively.t is time and x spatial coordinate.i and j are dummy indices.δijis the Dirac delta function and D is the mass diffusivity.The unclosed subgrid-scale (sgs)terms,including shearstresses(),energy flux(),and scalar mixing flux(),are modeled using a compressible- flow version of the Smagorinsky static model.For non-reacting flows,the scalar(φ)represents species mass fraction and the source term()is zero.For reacting flows,the selection of the scalar depends on the specific combustion model employed.Direct integration of finite-rate chemistry considers species mass fractions as a set of scalars.In a steady laminar flamelet model,the mixture fraction is selected,and the source term disappears.The flamelet/progress variable model uses both mixture fraction and a progress variable.

2.2.2.Thermodynamics and transport properties

Real- fluid properties need to be accurately calculated.According to fundamental thermodynamics theories,thermodynamic properties can be expressed as the summation of an ideal-gas counterpart and a departure function accounting for dense fluid corrections.23Transport properties of the mixture,including thermal conductivity and dynamic viscosity,are evaluated using extended corresponding state principles.Detailed validation and implementation are outlined in Refs.23,26.

An Equation Of State(EOS)is required to obtain fluid volumetric properties(p-ρ-T)and to close the theoretical formulation,Eqs.(1)–(4).Several cubic EOSs are available for real fluids.27In the current study,a modified Soave-Redlich-Kwong(SRK)EOS28is employed for its validity over a broad range of fluid states and easy implementation.The filtered SRK EOS can be expressed in the form of compressibility factor(Z)and written as:

where R′and T denote the specific gas constant and temperature of a mixture,respectively.The unclosed sgs term is highly non-linear,with subgrid interactions of triple components,This term appears to be negligible for ideal gases(Z=1),but may become significant and comparable to the filtered term at real- fluid(high-pressure)conditions.25A well-developed model for psgsremains an open topic of research,and is thus neglected in the present study.

2.2.3.Turbulence/chemistry interaction

For the physical problems of concern,fuel and oxidizer are injected separately,and then mix and react in a diffusion controlled mode.The chemical time scale is assumed to be short compared to its diffusion counterpart,so that combustion takes place within asymptotically thin layers embedded in the turbulent flow.These layers are referred to as flamelets with well-defined inner structures.As a consequence,the chemistry is decoupled from the local flow dynamics and evaluated by means of solutions of counter flow diffusion flames,which are filtered using appropriate scalars with presumed probability density functions and tabulated into a flamelet library.The selected scalars depend on the specific flamelet model implemented.Both steady laminar flamelet and flamelet/progress variable models are employed.Detailed information can be found in Huo and Yang.24

2.2.4.Numerical method

The numerical framework is based on a preconditioning scheme and a unified treatment of general- fluid thermodynamics.26It employs a density-based, finite-volume methodology,along with a dual-time-step integration technique.29Temporal discretization is achieved using a second-order backward difference,with the inner-loop pseudo-time integration by a four-step Runge-Kutta scheme.Spatial discretization is obtained with a fourth-order central difference scheme in generalized coordinates.Fourth-order matrix dissipation is employed to ensure numerical stability and minimum contamination of the solution.Finally,a multi-block domain decomposition technique associated with the message passing interface technique is applied to optimize computation speed.

2.3.Emulation

The emulation employs a GP regression technique called Kriging,combined with data-driven basis functions.These eigenmodes represent the coherent structures underlying the flow dynamics.The framework incorporates sensitivity analysis of design parameters using Sobol’indices,30physics-guided data partitioning,and flow evolution prediction.The novelty of the approach is to build the emulator using POD,allowing for data-reduction and extraction of coherent structures.

Typically,POD is only suitable for extracting coherent structures at a single geometry,whereas for emulation,a versatile method is needed to extract common structures over varying geometries.To this end,a common grid system is established for the projection of all simulation data.The Common POD(CPOD)is thus formulated to capture the flow characteristics over the design space.The Kriging model is essentially an interpolator for the time-varying coefficients of the obtained POD basis functions.This methodology allows for accurate flow predictions at any new design setting.As mentioned previously,DOE determines the number of design points and associated parameter sets for which high- fidelity simulations are conducted.The accumulated database is used to train the emulator.Note that different design points may show either similar or significantly different flow structures.To better integrate the flow physics for the CPOD-based emulation,two techniques are implemented beforehand:(A)a sensitivity analysis for identifying important design parameters,and(B)a decision-tree learning process determining the dichotomy of designs with distinct features.

2.3.1.Kriging surrogate model

The predictive model(emulator)combines machine-learning techniques and statistical modeling with a physics-driven data reduction method.A complete description of the model development from the statistical perspective is given in previous studies.20,31The model relies on the POD basis functions,also known as mode shapes,which are the spatial distributions representing the coherent structures of the flow field.It should be noted that this calculation is not done for the entire dataset,as each physical parameter is processed separately.In order to treat the data together,scaling and dimensions need to be carefully formulated to obtain interpretable mode shapes.

To accommodate different geometries in the design space,a common set of mode shapes is required for building the emulator.Physically,this means that common coherent structures must be extracted over the design space,which includes broad geometric variations.One option is to select a computational domain that stays the same despite design changes.32As previously mentioned,an emulator can be formulated as long as a set of common basis functions exist,leveraging the eigenfunctions generated by the POD analysis.Algorithmically,the CPOD expansion is obtained by first rescaling the various cases to the same grid,then computing the POD expansion,and finally rescaling the resulting modes back to the original grid.The details for CPOD can be found in Ref.31.

Suppose n simulations are conducted at varying design geometries c1，c2，...，cnand let f( x ，t;ci)be the simulated flow field at design cifor a given time t and spatial coordinate x.The kth CPOD mode is defined as

Here,the map Mi:R2→R2is the transformation which linearly scales spatial features from the common geometry c to the ith geometry ci.The sequence of POD coefficients is defined as:

with the corresponding POD expansion using K modes given by:

The transformation allows for the calculation of the CPOD.The obtained modes can be used to pinpoint important mechanisms of flow dynamics.

The calculation of the inner product is a computational bottle-neck,requiring eigen-decomposition of a nS×nS matrix,where n is the number of simulated cases and S the number of snapshots.This usually requires O(n3S3)computational work.An iterative method of eigen-decomposition based on periodic restarts of Arnoldi decompositions is used to quickly calculate the first few eigenvectors with the largest eigenvalues.

A Kriging model is applied to the CPOD time-varying coefficients of the CPOD modes, βk(ci，t).For the fine temporal resolution typical of LES(～10-6s),there is no practical need to estimate temporal correlations,especially because predictions will not be made between time-steps.The time independent emulator uses Kriging models at each instant of time.With the mean and variance computable in closed form,uncertainty quantification and confidence intervals can be calculated easily.Such an emulator minimizes the Mean-Squared Prediction Error(MSPE),a commonly-used criterion.In the context of flow field prediction,this Kriging estimator allows us to obtain accurate flow predictions from the CPOD time varying coefficients.It can also be shown that this best MSPE predictor is unbiased,matching the expected and true function value.33

To close the formulation,the model parameters need to be tuned using data.A technique called maximum likelihood estimation,an estimation technique widely used in the statistical literature,34is employed and optimization is achieved by means of the L-BFGS algorithm.35Once the model is trained,the emulator is used with the CPOD expansion to predict the flow evolution at a new design point,that is,

The computational cost of the proposed emulation is three orders of magnitude smaller than that of LES.20

2.3.2.Sensitivity analysis

A sensitivity analysis using Sobol’indices30is performed to determine which design parameters contribute most to changes in the output responses of interest.The analysis allows for parameter reduction.The idea is to decompose the variations of certain output variables into the partial variations attributable to each input parameter and the effects of interactions between parameters.Such a method is closely related to the classical analysis-of-variance technique used in linear regression models.36

Sobol’indices can be computed as follows.First,a pseudorandom parameter sequence is generated using a low discrepancy Sobol’point set.Then,this sequence is used to estimate the integrals,which provide the corresponding Sobol’indices.20The quantification of the response sensitivity for each parameter serves two purposes:(A)it provides a preliminary analysis of important effects in the system,which facilitates further physical investigations,and(B)it reduces the number of parameters that must be considered in the emulator,enabling efficient survey of design parameters within the design space.

2.3.3.Decision tree

The flow field may display significantly different structures at different design points.For the case of swirl injectors in the present study,there exists a jet-like/swirling flow dichotomy determined by the liquid- film spreading angle in the design space.For simulated design points,it is trivial to classify whether such a parameter set results in a jet-like or swirling flow,because the flow field data is readily available.For design settings that have not been simulated,a data-driven technique is needed to make such a classification.With this technique,a boundary between jet-like and swirling cases can be quantified over the design space of interest,and this enhances physical insight into the design space and can guide additional experiments.Furthermore,the classification information can be used to train separate surrogate models for the jet-like and swirling domains.This partitioning of the dataset allows the model to extract flow characteristics associated with jet-like or swirling behavior separately,thereby improving its predictive accuracy.A machine-learning tool‘‘decision tree” is implemented for the classification process.

Decision trees are one of the most popular predictive models in data mining and machine learning.37A decision tree is a support tool that models parameter settings and their possible consequences.Such methods are a part of a larger class of learning methods called supervised learning,38which aims to predict an objective function from labeled training data.A classification tree specializes in predicting classification outcomes,such as whether a parameter set has a jet-like or swirling flow.The trained model can be summarized by a binary tree,separating the design space into two subgroups.Each node of this tree represents a parameter decision,and each leaf of the tree indicates the class of outcomes,following the chain of decisions made from the tree root.

3.Case study:Swirl injectors

In this section,a case study of liquid swirl injectors is performed to illustrate the proposed design methodology with the combined LES-based simulations and POD-based emulations.The former are used to investigate the detailed spatiotemporal flow structures and flame dynamics in a high- fidelity manner and to identify important injector design parameters according to their effects on propellant mixing,flame stabilization,and thermal protection.The latter further explore the design space and pinpoint the optimal group of design parameters,in subtantially reduced turn-around times.

3.1.LES-based high- fidelity simulations

The LES-based framework presented in Section 2.2 is applied to simulate supercritical mixing and combustion in swirl injectors.Flow swirl has been widely used in modern propulsion and power-generation systems.39,40The swirling motion induces outward spreading of the liquid film and produces a central recirculation zone downstream of the injector,thereby improving mixing efficiency and flame stabilization.As described here,high- fidelity simulations of three different configurations,including simplex swirl injector,41bi-swirl injector,42,43and Gas-Center Liquid-Swirl Coaxialinjector(GCLSC),44were performed to facilitate understanding of physicochemical processes and identify important design parameters for injector performance.

3.1.1.Simplex swirl injector

The simplex swirl injector of concern is the inner swirler of a bi-swirl injector used in RD-0110 rocket engine.45Fig.4 shows a longitudinal view of a bi-swirl injector element.43Liquid OXygen(LOX)is tangentially injected into the inner swirler,while kerosene is tangentially introduced into the coaxial outer annulus.They mix and react in the downstream region of the injector.

Fig.4 Schematic of single injector element.43

The geometric parameters and operating conditions are adapted from the RD-0110 engine.45r and Rvdenote radial coordinate and vortex chamber radius,respectively.A LOX post with a thickness of h(0.8 mm)is recessed to a distance of l(1.5 mm),and the width of the coaxial annulus is Δr(0.5 mm).The injector measures length L of 22.7 mm and nozzle diameter R of 2.7 mm.As will be shown in Section 3.1.2,these parameters are crucial for efficient mixing and combustion.The operating pressure is 100 bar(1 bar=105Pa),far exceeding the thermodynamic critical points of oxygen(50.5 bar)and kerosene(21.7 bar).In this section,attention is focused on the dynamics of the LOX swirling flow in the inner swirler without influence from the outer annulus.

Fig.5 shows a snapshot of the density field in both the axial and azimuthal directions.LOX is injected into the vortex chamber at 120 K.Many salient flow characteristics are observed.41The swirl-induced centrifugal force drives the LOX film to flow along the injector surface.A center gaseous core is formed because of conservation of mass and angular momentum.The axial velocity of the LOX film increases significantly through the converging section between the vortex chamber and nozzle.This leads to a much thinner and more uniform LOX film in the nozzle than in the vortex chamber.The thin LOX film spreads upward and mixes efficiently with the surroundings.The swirl strength of the liquid film decreases as it convects downstream,resulting in an adverse pressure gradient and a center recirculating flow.

Fig.5 Snapshots of density field in axial and azimuthal views.

In spite of the relatively simple geometry,there exist several different types of flow instabilities in the flow field.For example,pressure disturbances downstream of the injector,which could be triggered by the liquid- film shear-layer instability,travel upstream to the tangential inlet in the form of an acoustic wave.Such disturbance then causes the incoming mass flow rate to fluctuate at the inlet,due to the variation of the pressure drop across the inlet.The resultant mass- flow-rate fluctuation propagates downstream in two distinct ways:one along the axial direction and the other in the azimuthal direction.The calculated injector dynamics show close agreement with classical theories.46Detailed discussion of the underlying physics is given in Ref.41.

3.1.2.Liquid-liquid bi-swirl injector

This section presents LES results on the flow and combustion dynamics in an RD-0110 liquid-liquid bi-swirl injector,as shown schematically in Fig.4.Kerosene is injected into the coaxial annulus at a temperature of 300 K.Special attention is paid to the effects of recess region(l),post thickness(h),and annulus width(Δr)on the mixing and combustion characteristics.42

Fig.6 shows snapshots of the density(ρ),vorticity(|ω|),and kerosene mass fraction(ykero) fields.The development of the liquid film in the inner swirler resembles the situation in the simplex swirl injector shown in Fig.5.Large vortical structures are observed in various regions,including the wall boundary layers,the interfacial layer between the dense LOX and gaseous oxygen,and the fluid mixing region.The mixing of LOX and kerosene begins in the recess region.Given that the momentum flux of LOX is roughly five times of that of kerosene,the LOX stream spreads upward,forms a conical liquid sheet,and blocks the kerosene flow,which then adjusts its path and occupies the upper part of the recess region.The LOX film surface is highly wrinkled by shear-layer instability.Classical liquid breakup does not occur at supercritical conditions,where it is replaced by turbulent mixing and diffusion,through which efficient mixing of LOX and kerosene takes place.42

Fig.6 Snapshots of density,vorticity magnitude,and kerosene mass fraction fields(non-reacting flow).

To identify and quantify the importance of injector design parameters,a parametric study was conducted to explore the effects of recess length,post thickness,and annulus width on the mixing and combustion characteristics.Four cases were performed with the same operating conditions.Cases 2–4 differ in only one geometric parameter from Case 1(baseline).The recess region is removed in Case 2;the post thickness is increased to 1.3 mm in Case 3;and the annulus width is doubled to 1.0 mm in Case 4.Fig.7 shows the effects of these parameters on the distributions of the kerosene mass fraction.The presence of a recess region(Cases 1,3,and 4)is found to advance the interaction of the propellants within the injector and improve the mixing efficiency.Furthermore,because of the lack of the restriction of the outer annulus surface in Case 2,kerosene spreads upward,leaving an insufficient amount of fuel in the wake of the inner post for mixing with LOX.For Case 3 with a thicker post,a larger spreading angle is generated for the LOX steam.The mixing is significantly enhanced in Case 3,due to the wider area interaction and larger vortical structures in the recess region.Similar phenomena are observed for Case 4 with a wider annulus.

Fig.7 Instantaneous distributions of kerosene mass fraction in injector near- field for all cases(non-reacting flows).

Fig.8 Snapshots of temperature field for all cases(reacting flows).

Simulations of reacting flows were performed to investigate the effects of injector design parameters on flame dynamics.Fig.8 shows the instantaneous distributions of temperature near the injector exit.For all cases,the flame is anchored in the recess region and further stabilized by the center recirculating flow.In Cases 1 and 2,the flame is slightly lifted off the LOX post,with a thin flamelet attached to the lower post tip.In Case 3,the flame is anchored to the lower part of the post surface.A thicker post leads to a broader region for reactant mixing and combustion,but the resultant exposure of the post surface to hot products increases the thermal loading.This is not desirable from a practical design perspective.The situation is even worse for Case 4 with a wider annulus;the flame covers the entire surface of the LOX post,rendering the hottest temperature profile among all cases.

With these results,our understanding of mixing characteristics and flame stabilization is substantially improved,and important design parameters that affect the injector performance are identified.43The question remains how to determine an optimum group of design parameters to ensure the best performance.The issue can be effectively addressed using emulation techniques.

3.1.3.Gas-centered liquid-swirl coaxial injector

The third injector configuration presented here is a GCLSC,which was used in the main combustion chamber of the RD-170/180 engine for the Energia and Atlas V launch vehicles,47,48and the most powerful liquid rocket engine to date.Fig.9 shows a schematic of the longitudinal view.49Gaseous OXygen(GOX)is axially delivered into the center tube,and liquid kerosene is introduced through the tangential inlet in the coaxial outer annulus.Propellant mixing occurs in the recess region of length of Lr.Three cases with different recess lengths are discussed in this section.The GOX post is fully recessed with Lr=16mm for Case 1;partially recessed with Lr=10.5mm for Case 2;and not recessed for Case 3.The operating pressure is 253 bar.The inlet temperatures of GOX and kerosene are 687.7 K and 492.2 K,respectively.Kerosene undergoes a thermodynamic change of fluid state from compressed liquid at injection to supercritical fluid in the flame region,while GOX stays supercritical.44

Fig.10 shows global and zoomed-in views of snapshots of the water mass fraction(yH2O) field with different recess lengths.For all cases,the flame is anchored at the GOX post tip,the axial location of which increases with decreasing recess length.For Case 1,the kerosene resembles a swirling jet in cross flow.This leads to the formation of a shear layer at an earlier stage and enhances the propellant mixing significantly.As a result,Case 1 produces a broader flame area than Cases 2 and 3 at the exit of the recess region.The intensive flame zone flushes the annulus surface,by means of turbulent motion and thermal diffusion,thereby increasing the risk of thermal failure of the injector.For Case 3 without recess,the flame ignites downstream of the injector.The swirl-induced centrifugal force drives the kerosene flowing along the taper surface,rendering very limited mixing between GOX and kerosene.The flame is restrained near the taper surface.The majority of the central GOX stream moves downstream without interaction with kerosene.As the recess length increases,fuel entrainment improves and propellant mixing is enhanced.The trade off is,however,a less fuel-rich mixture and a higher temperature along the injector surface with increasing recess length.The high-temperature profile along the surface endangers the hardware and/or elevates the cooling requirement to maintain proper operation of the injector device.On the other hand,Case 2 achieves a good balance between efficient mixing in the recess region and thermal protection of the annulus surface.The optimized recess length can be determined by the proposed emulation tool.

3.2.CPOD-based emulation for simplex swirl injector

As an example,the emulation framework is demonstrated using the spatiotemporal evolution of the non-reacting flows in a simplex swirl injector.Fig.11 shows schematically the injector and Table 1 presents the ranges of design parameters:length(L),injector radius(Rn),injection angle(θ),injection slot width(δ),and axial location of the slot(ΔL).LOX is injected tangentially into the injector at 120 K with a mass flow rate of 0.15 kg/s.The injector is initially filled with gaseous oxygen at 300 K.The operating pressure is 100 bar.The 6P rule50(within(5–10)P rule of thumb with P being the number of design parameters)is applied for DOE,yielding a total of 30 design points.MaxPro is then implemented to obtain the 30 design points in the parameter space.20All design points are treated as training points for high- fidelity simulations with the same operating conditions.The collected simulation data is analyzed and used to build the surrogate model.

Fig.9 Schematic of GCLSC.49

Fig.10 Global and zoomed-in views of instantaneous distributions of H2O mass fraction(reacting flows).

Fig.11 Schematic of swirl injector.

Table 1 Design ranges for swirl injector parameters.

3.2.1.Sensitivity analysis

Liquid- film thickness and spreading angle are two vital injector performance metrics.An inviscid,incompressible- flow theory estimates these responses as a function solely of the geometric constant.46To quantify the importance of each injector parameter on the liquid- film thickness and spreading angle,a sensitivity analysis using a Monte Carlo approximation of Sobol’indices was conducted.30Fig.12 shows the results of this analysis.The primary contributing parameter was circled with solid lines.The slot width(δ)is found to be the strongest factor for the spreading angle.Assuming a fixed mass flow rate,the inlet velocity is inversely proportional to the slot width,and smaller slot widths would have larger liquid- film momentum.Intuitively,the injection angle also directly affects the momentum direction.As the angle increases,increased azimuthal momentum widens the spreading angle at the injector exit.This is not reflected in the present analysis.

Fig.12 Sensitivity analysis of liquid- film spreading angle.

3.2.2.Decision tree

Analysis of simulated design points shows a distinction between two underlying physical phenomena.One is the expected swirling film that spreads radially upon exiting the injector.The other is a jet-like behavior of the liquid film where the radial spreading is minimal.A classification tree can be trained using the Gini impurity index(see Ref.38for details).The simulated flow field of each sampled design point is examined and classified as either jet-like or swirling flow.Next,a search is conducted over all the design parameters and possible split-points, finding the parameter constraints which minimize misclassification.A branch is then made in the classification tree corresponding to the parameter constraint,and the same branching procedure is repeated for each of the resulting child nodes.This decision tree learning technique not only provides a means for partitioning the training dataset for the model into jet-like and swirling flows,it also reveals physical insights into the important design parameter constraints causing the jetswirl dichotomy.

Fig.13 shows the decision tree splitting process,20indicating how the algorithm decides how an injector parameter is associated with either jet-like or swirling flow.The initial decision between the two behaviors is achieved by assessing the extent to which the liquid film spreads radially from the injector exit.The numeric outputs are binary flags for the two subgroup classifications.For example,the first numeric output,θ＜ 60.0°,divides the dataset into 11 jet-like and 19 swirl cases.The decision tree then further categorizes the data according to the injector inlet and radius.The decision tree quantifies these effects and predicts a jet-like injector with θ ＜ 60.0°and δ ≥ 1.40 mm.Following the previous two criteria,if the tangential inlet angle is large enough,that is,θ ＞ 49.2°,the injector retains swirling behavior.Although this model cannot be directly used to facilitate design decisions,its usefulness lies in the fact that it can manage the quality of training data by only using the relevant design points for a designated classification.

Fig.13 Decision tree splitting process with numeric classifiers.20

3.2.3.Inverse problem optimization

The surrogate model can also be used to find the design geometry for a specified performance measurement,such as a specific liquid film thickness and spreading angle.With the trained regression model,the corresponding response can be predicted for a set of given parameters.On the other hand,for a specific response,an inference can be made about the new set of parameters.The relationship is determined from a calibration dataset,and the new parameter set can be solved through the regression model.Fig.14 shows a five-dimensional contour plot that illustrates a set of the candidate injector configurations(parameters normalized)for a desired liquid film thickness of 0.63 mm and spreading angle of 41°.The chosen initial points for the solver lead to convergence to a candidate injector configuration that would produce the desired responses.This provides an array of design geometries that can be further narrowed following more performance measurements or analysis of flow dynamics.

With specified constraints,an optimal configuration can be acquired.For example,if a liquid film thickness of 0.60 mm and spreading angle of 42.5°was desired for a first-stage engine injector longer than 50 mm and tangential inlet less than 1.50 mm,the best candidate injector would have the dimensions L=80.21 mm,Rn=2.52 mm, θ =62.43°,δ =1.16 mm,and ΔL=1.88 mm.

3.2.4.Spatiotemporal emulation

Fig.14 Five-dimensional contour plot for candidate injector configurations with a desired liquid film thickness and spreading angle.

Fig.15 Emulated and simulated instantaneous temperature fields(t=21.75 ms).

To ensure that the proposed emulator provides accurate flow predictions,we perform a validation simulation at a new geometric setting:L=22 mm,Rn=3.215 mm,ΔL=3.417 mm, θ=58.2°,and δ=0.576 mm,a 10%deviation on the existing injector used in RD-0110 engine.Fig.15 shows the qualitative comparison of the emulated and simulated temperature fields.From visual inspection,the predicted flow closely emulates the simulated flow field.Downstream recirculation zones are correctly identified in the prediction.These comparisons demonstrate the effectiveness of the emulator in capturing key flow physics and the importance of incorporating known flow properties of the fluid as assumptions in the statistical model.

The Root-Mean-Square-Relative Error(RMSRE)is calculated to measure the accuracy of the emulations.It quantitatively compares the temperature distribution between simulation and emulation for two cases(swirl and jet-like),illustrating minor discrepancies near the injector wall.The swirl case has an overall error of 5.18%,compared to 6.62%upstream and 3.10%downstream of the injector exit.For the jet-like case,the error varies from 8.30%to 9.03%if the considered area changes from upstream to downstream of the injector exit.

Injector dynamics involve downstream pressure fluctuations causing pressure drop oscillations across the liquid film.These changes in turn trigger mass flow rate variations across the tangential inlets,40over a wide range of time scales.A Power Spectral Density(PSD)analysis can quantify these oscillations and capture the periodicity of flow features.Pressure PSDs are calculated for both the simulation and emulation results.Fig.16 shows the PSD of two probes along the axial direction;the dominant frequency content is observed to be well quantified.For system dynamics,retaining spatiotemporal information is critical to properly identifying injector tuning characteristics.Combustion instabilities have plagued rocket engine development,and a spatiotemporal emulator would be vital to surveying how flow and combustion dynamics vary in the design space.

The emulator model also allows for quantification of predictive uncertainty,which can be used as a goodness-of- fit test.Moreover,these uncertainties can be linked to dynamic flow physics.As an example,the spatial uncertainty quantification is shown in Fig.17,showing the one-sided width of the 80%pointwise confidence interval for pressure and temperature20(a derivation of this interval is found in Ref.31).It is seen that the emulator is most certain in predicting the flows near the inlet and centerline of the injector.The uncertain areas,in the time-mean temperature distribution,correspond to the most dynamic sections of the liquid transition region.The downstream uncertainty is caused by the recirculation induced through vortex breakdown.

Fig.16 PSD of pressure fluctuations from simulation and emulation data at different locations.

Fig.17 One-sided width of 80%confidence interval:Temperature and pressure predictions.20

3.2.5.Improvement on CPOD-based emulation

The CPOD-based emulation was examined in spatiotemporally evolving flows of swirl injectors with five-parameter design space.The emulator was built using the training database of 30 LES-based simulations,each of which requires six days of computation time on a parallelized system of 200 Intel Xeon E5-2603 1.80 GHz processing cores.While the process to accumulate this dataset is undeniably time-consuming,the proposed surrogate model can provide a good prediction of output performance in slightly over an hour of computation time.Fig.18 presents the computational timeline for the whole design framework.An LES-based simulation requires nearly 30000 CPU hours to collect enough data for physics extraction and POD analysis,while the parallelized predictions from the emulator only need around 30 CPU hours,significantly reducing the turn-around time by three orders of magnitude.

One may wonder that the very fine structures are not captured exactly on the surface of the liquid film,as manifested in Fig.15.This is attributed to the assumption of identical POD modes for all design points in the common grid system,provided the design space is very large(Fig.11).The POD analysis of the whole 30-case database introduces a type of averaging effect on the flow dynamics,and thus smooths the prediction by the surrogate model.

To faithfully capture the spatiotemporal flow dynamics,an improved surrogate model,called Kernel-Smoothed POD(KSPOD),51can be adapted to the current high- fidelity framework.The key idea of the KSPOD is to retain the separate POD modes of the flow field for all training design points,and then apply Kriging to predict the weight(^wi)of each POD mode at a new design setting.These weights are subsequently used to predict the new POD modes through a weighted average of the extracted modes and coefficients at the new design settings,as follows:

For each time step and each mode,the kriging procedure is performed on both time-varying coefficients and weights of POD modes with given input parameters.

Fig.18 Computational timeline for design framework.20

Fig.19 Comparison of density field between LES-based simulation and KSPOD-based emulation.51

To demonstrate the function of KSPOD,a new database is established using simplex swirl injectors.From sensitivity analysis,injector length and radius play minor effects on the output responses.Therefore,only three parameters,injection angle,slot width,and axial distance of slot,are included in the design space.A total of 30 design points is determined with the 10P rule(P=3)and distributed using SLHD.The overall design matrix contains five slices,and each slice includes six design points.Following the flowchart in Fig.3,high- fidelity simulations are performed at all design points to create the database,which can be clustered into four subgroups through careful learning of the physical responses.51Fig.19 shows a comparison of density field between LES-based simulation and KSPOD-based emulation at a test point in one of the subgroups.The evolution of the liquid film and its spreading downstream of the injector exit agree well between the simulation and emulation.The small-scale structures are much better captured here than using the CPOD methodology.

The proposed methodology can be incorporated into a software for similar spatiotemporal problems.With respect to R and Python,the two most popular open source programming languages used by data analysts and data scientists,the methodology can be implemented in a straightforward manner.Existing packages,such as pyDOE and SLHD,can construct space- filling experimental designs and assess their quality.Established tests of the modred and pyKriging packages enable CPOD-based emulator model building,which is also reflected within R,mirrored by the bigpca and GP fit packages.These open source packages provide the key components such that the methodology can be incorporated into a software that can be practiced by others.

4.Conclusions

The present work proposes a high- fidelity methodology for design and optimization using LES and emulations.The framework gathers a group of methods,including DOE,LES,machine learning,POD-based emulation,inverse problem optimization,and uncertainty quantification.Given a set of design parameters,DOE determines the number of design points that are required to perform LES-based simulations.These simulations can capture spatiotemporal flow structures and flame dynamics and identify important design attributes,but they are time-consuming and become impractical for surveying the entire design space.The POD-based Kriging surrogate model(emulation),trained by the accumulated LES dataset,can efficiently explore the design space while maintaining high- fidelity spatiotemporally.The developed framework can significantly improve the knowledge base for the initial design stages in a very reliable and time-efficient manner.

As a specific example,the framework is implemented to study the liquid swirl injectors broadly used in aerospace propulsion and power-generation systems.Detailed flow and dynamics for three different types of injectors are examined using high- fidelity LES.Important injector design parameters are identified in terms of their influence on the effectiveness of mixing, flame stabilization,and thermal protection.Emulation is then used to survey the entire design space.To accommodate different injector geometries,a common grid system is constructed for CPOD analysis.The accuracy of the emulation is validated,and the uncertainty of prediction is quantified.The turn-around time of CPOD-based emulations is three orders of magnitude lower than that of LES-based simulations.Although the CPOD-based emulator predicts the mean flow features and certain flow dynamics at new design points quite well,some small structures are difficult to capture because of the nature of the CPOD technique.An improved surrogate model,the KSPOD-based emulator is developed to more faithfully capture the spatiotemporal flow dynamics by leveraging Kriging-based weighted functions to the POD modes at new design points.

Acknowledgement

This work was sponsored by the William RT Oakes Endowment of the Georgia Institute of Technology.