基于ECC的三叉树群组密钥协商方案

曾继强 史国振

1(西安电子科技大学通信工程学院 陕西 西安 710071)2(北京电子科技学院 北京 100070)

0 引 言

对于语音、视频会议等群组会话中，在不安全的网络上进行通信，需要一种高效的密钥协商协议来保证通信安全。在一个网络中，n个成员在一个群组中进行通信。这n个成员必须能够以安全的方式在公共信道进行通信，保证群组之外的用户都不能监听合法成员之间的对话。安全群组通信的一般旨在在小组成员之间建立一个保密通信的共享会话密钥。尽管CCEGK[1]，TGDH[2]，STR[3]采用了树形结构实现了密钥的协商，但是都是基于二叉树和两方的Diffie Hellman密钥交换协议实现。文献[10]在其提出的协议中引入三叉树结构，并使用GDH.2[11]来限制群组的数量为3k，其中k是整数。为了提高加密的效率，基于椭圆曲线密码体制起到了非常重要的作用，因为它比现有的基于整数或整数分解的离散对数困难问题的方法具有更短的密钥大小，并且具有相同的安全级别。椭圆曲线公钥密码的使用是由Koblitz[12]在1987提出的，此后，对椭圆曲线密码进行了大量的工作。文献[20]将椭圆曲线密码算法加入到了群组密钥协商协议中，其使用的是基于二叉树的结构。文献[9]提出的群组密钥协商协议使用了椭圆曲线算法，并采用的三叉树的群组组织结构，成员之间的协商过程主要利用临时生成的随机数作为私钥并将私钥与一个大素数相乘作为公钥进行密钥协商。本文在文献[10]的基础上提出一种基于椭圆曲线算法的群组密钥协商协议，群组组织结构与文献[10]一样采用了三叉树结构，该协议对于成员的数量没有限制，解决了文献[10]对成员数量限制为3k的缺点，三叉树与二叉树相比在结构上更加简单，有利于减少密钥树的高度，使用三元树代替二叉树的优势在文献[10]已经证明。最后本文利用了双方椭圆曲线DH协议和三方椭圆曲线DH协议进行群组密钥的协商，与文献[9]使用公私钥对进行密钥协商相比计算复杂度更低。由于采用了三方密钥交换协议和三叉树结构，本方案具有密钥长度短计算量小等优势，在群组成员较大的情况下本文群组密钥协商协议与现有方案相比具有更高的效率。

1 相关知识

文献[14-17]提出了几种群组密钥协商方法。这些方法可以分为三类:集中式的、分散式的和分布式的。

在集中式的方法中，必须选定一个可信的实体(通常为群组服务器)进行密钥的生成和分发，在这种方法中最关键的是如何找到一个可信的实体，以及保证该实体始终可用，在安全性上一旦实体被攻击，整个群组的密钥将泄露，因此在可行性和安全性上没有优势。

分散式的密钥协商方法主要是将群组再进行细分成一个个小的子群组，每个子群组选择一个群组控制者来负责群组密钥的生成和分发，该方法的主要问题是当群组用户较多的时候，计算量将非常大，导致效率很低。

分布式的密钥协商方法中，密钥的协商是由群组成员共同协商完成的。Steiner等[11]扩展了Diffie Hellman协议基于Diffie Hellman群组密钥协商协议GDH(Group Diffie Hellman key agreement protocol)，这是一个可以应用在多方的密钥协商协议，该协议中具有n个用户的群组需要进行n轮的协商才能得到最后的群组密钥。特别是在具有大量群组组成员环境中，协商的次数是至关重要的，因为在成员进行协商完成之前，其他成员无法进行通信。

Kim等[17]提出了一种基于树的组密钥协议——TGDH。TGDH得到的组密钥需要二叉树中的所有组成员共同完成。与GDH相比，TGDH只需要常数轮便可完成密钥的协商，在计算量上具有一定优势。文献[10,21]基于TGDH提出了一些基于树的群组密钥协议,文献[10]第一次介绍三元树方法，并将GDH.2[11]作为在群成员中建立一个共享组密钥的基本手段。这一方法大大降低了树的高度，减少了计算和通信开销。但是这种方法的主要缺点是它只支持成员数量为3k的群组，k是任意整数。文献[9]对文献[8]进行了改进，虽然考虑了群组成员的变化，但是对于群组成员的离开没有进行详细的阐述。

2 预备知识

2.1 椭圆曲线密码学

椭圆曲线的一般形式为:

y2=x3+ax+b

在密码学中，椭圆曲线方程的变量和系数仅限于有限域上的元素。因此，对于上面的方程，x、y是群GF(p)的坐标，a、b是p的整数模，满足：4a3+27b2≠0(modp)，其中p是有限域上的一个模素数。在群GF(p)上的椭圆曲线E由两个方程所定义的点(x，y)和一个额外的点组成(通常为无穷远点)。

通常在两种有限域上定义椭圆曲线:一种是包含素数p的有限域Fp上，一种是以2为特征值的有限域上。本文采用第一种定义方式来实现密钥的协商。

在文献[6,12,14]详细描述了ECC的算法过程。ECC的安全性是基于椭圆曲线离散对数问题ECDLP(Elliptic Curve Discrete Logarithm Problem)。基于椭圆曲线离散对数问题陈述如下：给定素数P和椭圆曲线E，对Q=kP,在已知P,Q的情况下求出小于P的正整数k，已知k和P计算Q比较容易，而由Q和P计算k则比较困难。

2.2 双方椭圆曲线Diffie-Hellman协议

加入用户A和用户B进行密钥协商，双方椭圆曲线DH密钥协商协议步骤如下：

A生成密钥K=a1Y。

B生成密钥K=a2X。

2.3 三方椭圆曲线Diffie-Hellman协议

三方椭圆曲线Diffie-Hellman协议基于GDH[5]结合椭圆曲线实现了三方(A，B和C)的密钥协商，实现如下：

A、B和C分别选择自己的私钥a1、a2、a3并保密。

A计算出X=a1P并发送给B。

B计算出Y1=a2P、Y2=a2X并构造集合{X,Y1,Y2}发送给C。

C计算出K=a3Y2、Z1=a3Y1和Z2=a3X，把K当作群组密钥，并将剩余的Z1、Z2分别发送给A和B。

A和B在收到C发来的数据后计算出相同的群组密钥，其中：

A：K=a1Z1

B：K=a2Z2

在三个成员完成密钥协商后，椭圆曲线上有一个共同的点即：K=a3Y2=a1Z1=a2Z2=a1a2a3P。如果将此密钥用作会话密钥，则必须得到一个整数点。获取该整数有两种方法：可逆的和不可逆的[20]。如果需要将会话密钥解码为椭圆曲线中的一个点，则它是可逆的，否则就是不可逆的。可逆派生将产生一个会话密钥，它使私钥的长度加倍。在不可逆转的推导过程中，我们可以简单地使用x坐标或将x坐标进行简单哈希作为会话密钥。

3 本文方案

本文协议选择k比特的素数p和确定如下公共参数：{Fp,E/Fp,G,P}，其中：

E/Fp：有限域Fp上的椭圆曲线；

G:由E/Fp上点构成的循环群；

P：循环群G的生成元。

本文协议主要描述了N个成员如何共享会话密钥的初始化操作操作，并讨论了群组的动态变化操作，比如退出，加入等操作。

3.1 初始化

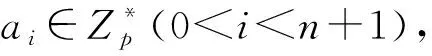
经过第一轮后每一个分组拥有自己的私钥(axi,ayi,azi)

每个分组中的一个成员作为下一轮的群组控制实体(GC)出现。本协议将选取第一个成员为组控制实体负责表示子群进行下一轮的协商。将每个子群看作是由每个GC控制的一个新节点。

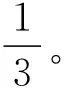
(4) 如果最后一轮剩下的节点不足三个，无法形成三叉树，则使用2.2中的双方椭圆曲线Diffie-Hellman协议来生成会话密钥。

下面我们通过一个例子来实现本文提出方案。假设一个群组中由12个成员组成，如图1所示。

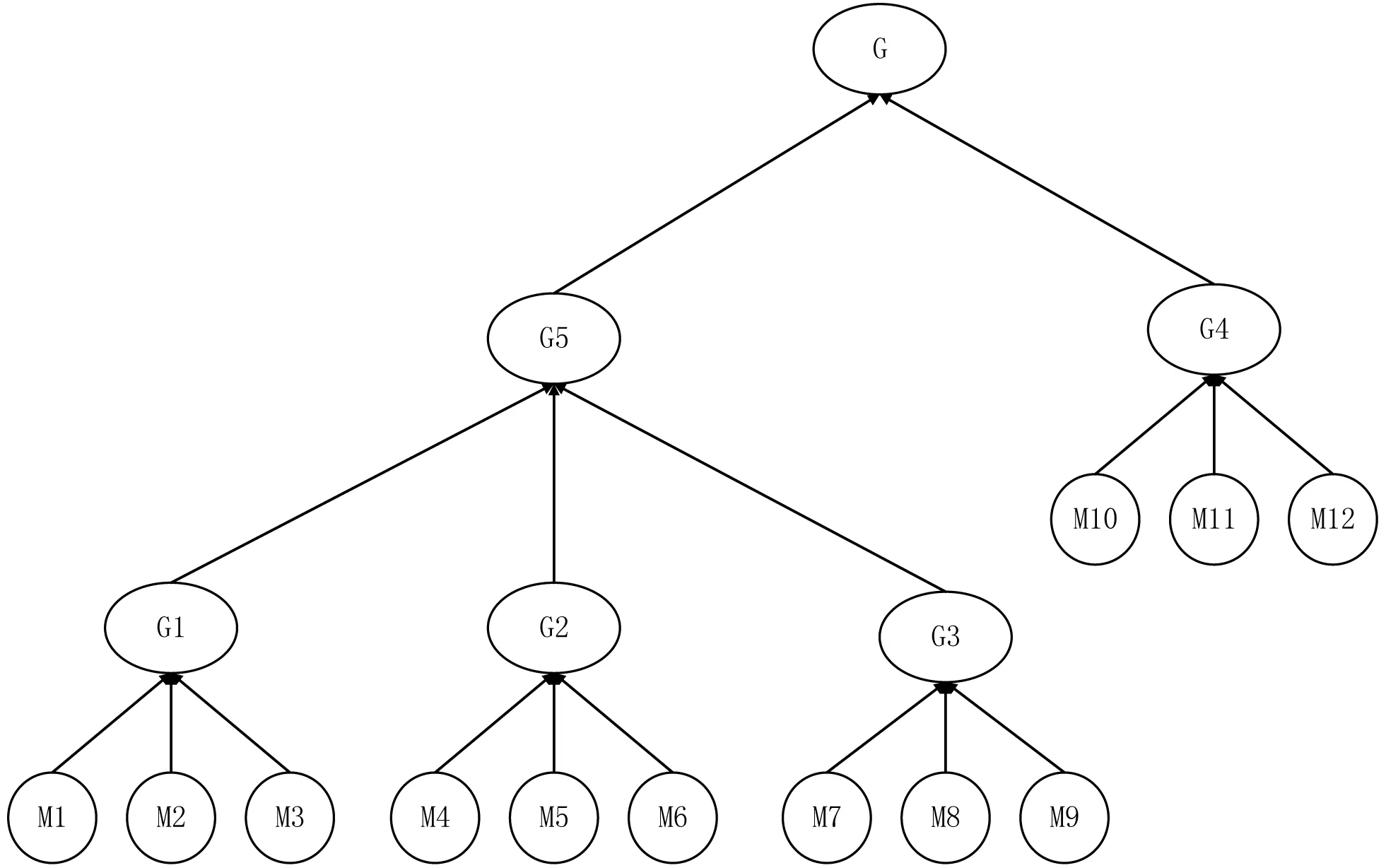
图1 12个成员的群组三叉树结构图

叶子节点M1,M2,M3,…,M12表示群组中的12个成员。在第一轮计算中，12个成员被分为四个子组，通过三方椭圆曲线Diffie-Hellman密钥交换协议形成会话密钥，并由G1、G2、G3、G4作为子组代表继续下一轮的计算；在第二轮计算中，由于有四个节点，因此在第二轮中只有G1、G2、G3参与协商，G4将在下一轮进行处理，在第二轮的协商中，按照第一轮的方法G1、G2、G3生成会话密钥，并由G5作为代表进行下一轮的协商；在第三轮的协商中，只剩下G5、G4两个节点，此时两个节点将通过双方椭圆曲线Diffie-Hellman密钥交换协议形成会话密钥，并由G作为根节点。最后G5、G4计算出的会话密钥为群组所有成员的共享密钥。在此过程中，群组中的通信次数和计算量最多情况如表1所示。

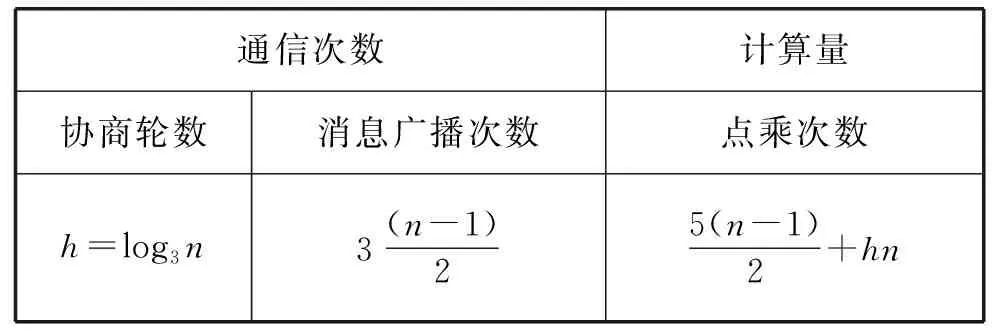
表1 通信和计算量

3.2 成员加入

高效的加入和离开处理方法对于动态组密钥协议非常重要，因为任何成员都可以随时离开和加入这个组。在本文中加入群组分为两种：一种是单个成员的加入，另外一种是多个成员同时加入群组。

3.2.1 单个成员加入群组

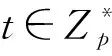
3.2.2 多个成员加入

假设有m个成员需要加入群组密钥为K的N个成员的群组中。操作步骤如下：

(1) 将要加入群组的m的成员通过3.1节的方法形成一个独立的群组，并协商出群组密钥假设为Knew。

(2) 将新的群组合并到要加入的群组中。

(3) 新的群组将群组密钥广播给要加入的群组的所有成员并生成新的群组密钥x1x2P，其中x1、x2表示两个群组合并之前各自的群组密钥。多个成员的加入需要进行消息广播次数为：

点乘的次数为：

式中：h,h′表示n个成员的群组和m个成员群组的三叉树的深度。在本文中，对点乘运算量是在最坏情况下的讨论，在实际的运算中点乘运算量比最坏情况下的小得多。

3.3 成员离开

如果是单个成员离开，我们可以通过多次的密钥协商重新生成群组密钥；如果是多个成员同时离开，此时的协商次数和计算量比较复杂，需将剩下的成员按照3.1节所示的方法重新初始化三叉树。

3.3.1 单个成员退出群组

单个成员退出群组时，必须从该成员到三叉树的根节点之间进行密钥更新。如果离开成员是子树的控制者GC(group controller)，则选择该子树中其他成员作为组控制者，而不需要改变其他子树的结构。假设具有n个成员的群组中成员m要退出群组，如图2所示。

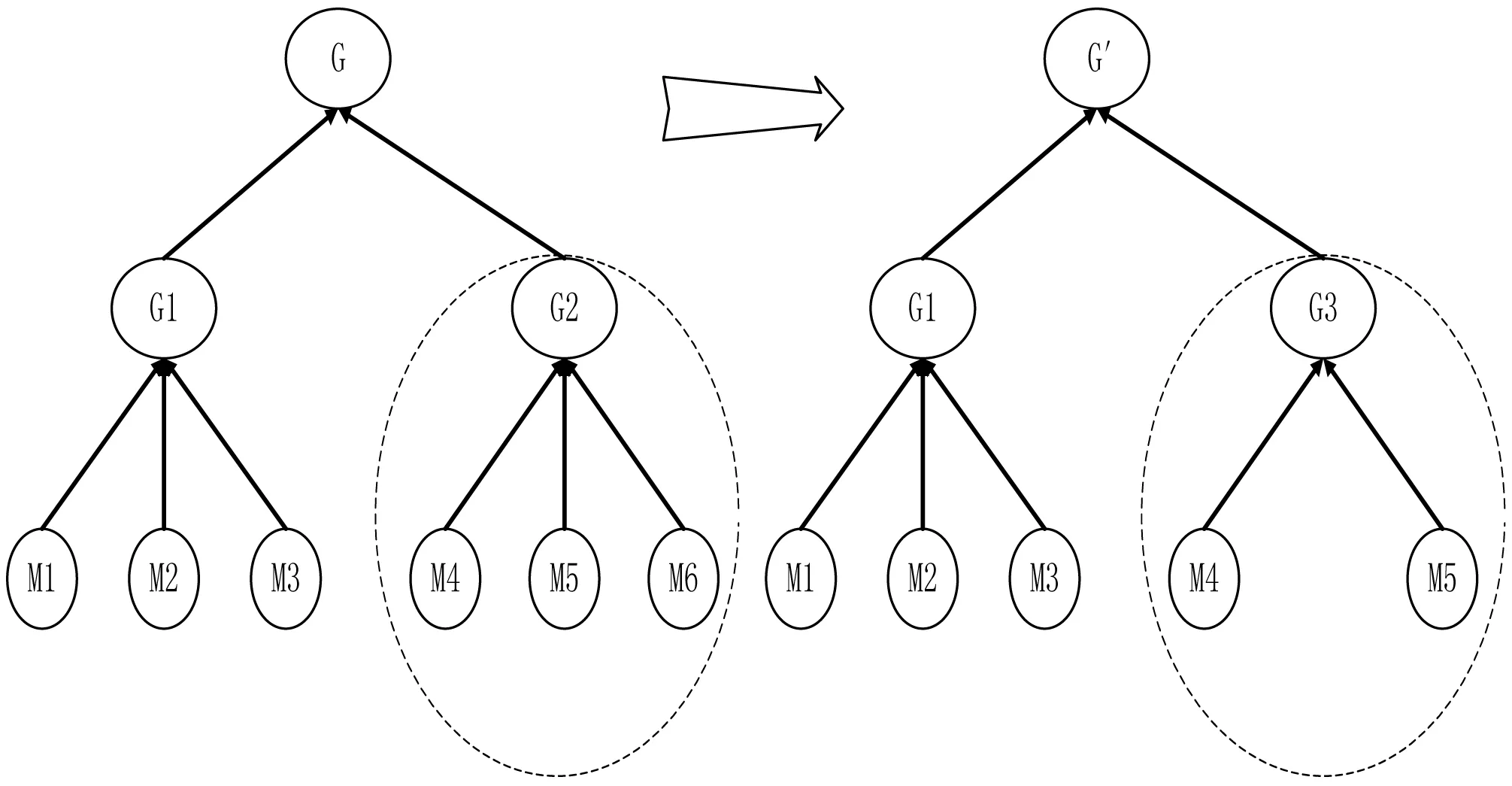
图2 成员m4离开过程

成员m4离开群组后，子树中剩下成员m5、m6，m5、m6通过双方Diffie-Hellman密钥交换协议重新协商群组密钥为k3，并选取m4为该子树的群组控制者，将k3P广播给子树G1，G1和G3通过双方Diffie-Hellman密钥交换协议得出新的群组密钥kG′=k1k3P，其中k1为子树G1原来的子组密钥，该密钥不需要重新协商。

成员离开所需要的计算量在最坏的情况下是成员处于三叉树的最深节点，密钥重新协商所需次数为n+3h-2。

3.3.2 多个成员离开群组

当有多个成员同时退出群组时，考虑到密钥的协商以及计算复杂度，本文对于多个成员离开采用的处理方法是将剩下的成员按照3.1节方法进行三叉树重新初始化。假设有n个成员的群组中有m个成员退出，则消息的广播次数为：

点乘次数为：

4 方案比较

本节将所提出的群组密钥协商管理操作与现有的基于二叉树的群组密钥协商技术进行比较。比较结果如表2所示，其中表中使用的参数如下：

n：表示一个群组中的成员数量；

m：表示要加入或者离开群组的用户数量。

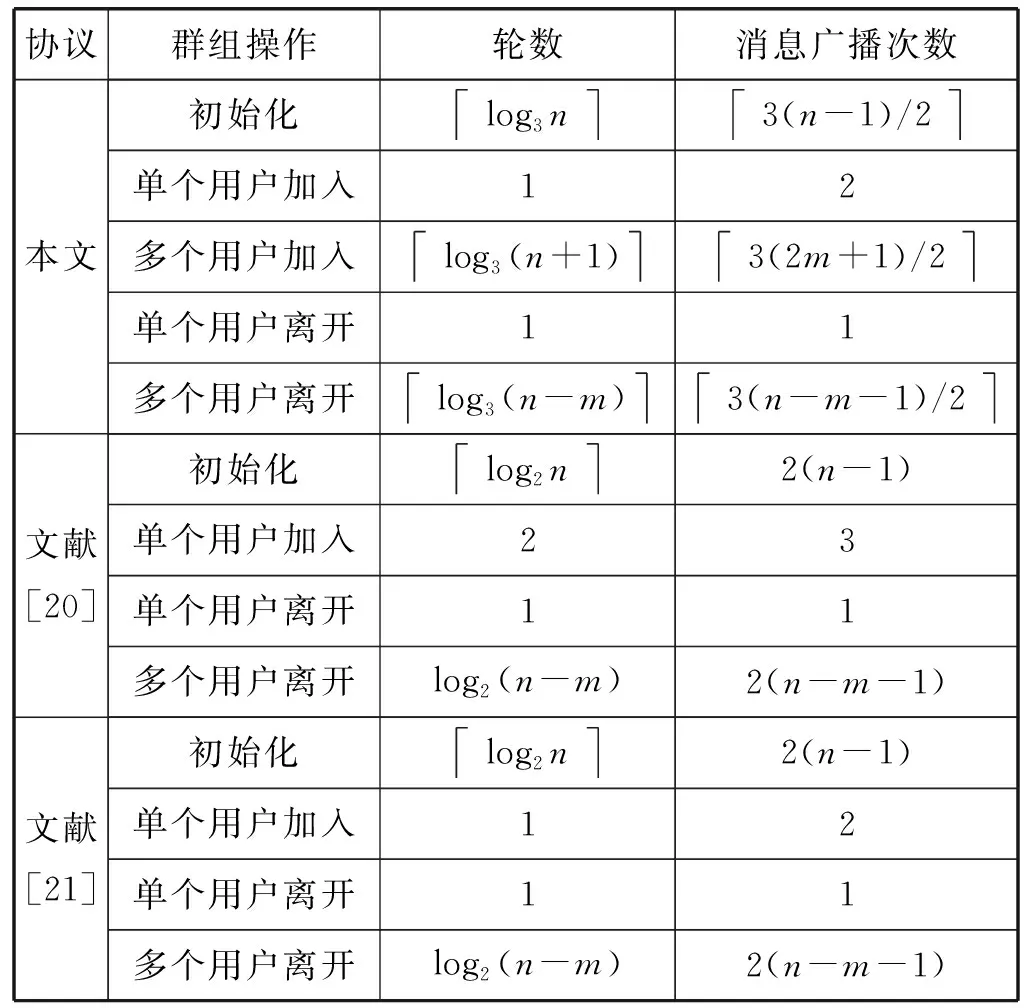
表2 性能分析

文献[20-21]对于多个用户同时加入的情况没有进行分析，本文所提出的方案还考虑了多个成员同时加入的情况。由表2可得本文所提出的协议在群组密钥初始化阶段密钥协商轮数、多个用户离开、初始化阶段的消息通信量以及多个用户离开情况下的消息通信量，与文献[20-21]相比，在群组用户数量较大的情况下有一定的优势，在效率上则优势明显。

5 安全性分析

(1) 密钥泄露安全性 密钥泄露是指当某个成员的密钥被攻击窃取后，攻击者只能冒充该成员进行群组会话，而其他成员的密钥依然是安全的。例如有两个成员m1、m2的子树，其中m1的公钥为X=a1P，m2的公钥为Y=a2P，则会话密钥为K=a1a2P，尽管攻击者获取了K、a1和P的值，但是仍然无法获取a2的值。

(2) 前向安全性和后向安全性 前向安全性是指新加入成员无法获取加入群组之前的群组密钥，因为密钥协商是基于离散度数问题，给定Q=kP，给定Q和P计算出k是困难的，而k是由子组组密钥点乘得到的，因此无法通过子组自己的群组密钥计算出群组密钥。后向安全性是指离开群组的成员无法再参与群组密钥协商，也不能得到后续的群组密钥，因为离开的成员从其所在的位置到根节点将重新进行密钥协商，因此后续的会话将使用重新协商的会话密钥进行通信，能保证后向安全性。

(3) 密钥控制 密钥控制是指群中任何合法的成员都不能决定或者影响群组密钥的值。在本文的方案中群组会话密钥是由群组所有成员共同协商完成，因此没有任何一个成员能控制或者提前决定会话密钥。

6 结 语

本文提出了一种高效的群组密钥协商协议。在本方案中使用三叉树来对群组成员进行分组来代替二叉树。群组密钥的协商采用基于ECC的三方Diffie-Hellman算法，本文主要描述了群组密钥的生成过程，并针对群组的动态变化对相应的密钥进行更新操作。在群组动态变化时，未变动的成员不需要再重新生成新的随机数，减少了群组变动的计算量。当某个用户收到攻击时，攻击者只能冒充该成员进行通信而其他成员不会收到影响，相比使用群组密钥分发方案更具有可靠性。最后将群组的各种操作的复杂度与现有的技术进行了比较，表明本方案比现有协议具有优势。本文的不足之处在于尚未对成员进行身份认证，在接下来的工作中，将继续研究对成员的身份认证以及成员之间的角色划分。