利用数学技巧处理斜面上的平抛运动
2018-09-26叶廷德
叶廷德
(福建省寿宁县第一中学,福建寿宁 355500)
引 言
近些年,我国对科学教育方法给予了足够的重视。教育部门推出的《普通高中物理课程标准 》中明确指出,高中的物理教学要让学生了解物理学科探索的过程和研究方法;同时,物理学科的教学目标也设定为培养学生自主完成科学探索过程,提升学生的自主学习能力,使学生养成良好的思维习惯[1]。在实际生活中,可以利用物理知识解释一些物理现象;同时,能够利用物理知识解决实际问题。另外,还针对物理教学设定了三维目标,即让学生经历科学探索、充分认识科学探索的实际意义、对探索方法和研究方法进行实际应用、最后验证物理规律的阶段。虽然,我国对科学教学方法的认识有所提升,并制定了相关的规范和政策,相关学者也对科学教育方法做出了多方面的研究,给出的教育方法具有一定的指导性,但是,缺乏一定的应用机制。教师在实际教学中,会根据相关标准的要求尝试改变教学方法,引导学生完成科学探索,但是实际的教学效果并不明显。究其原因就是针对科学教育方法的研究过少,无法真正掌握科学教育的精髓。鉴于以上问题,笔者以平抛运动这一物理问题为例,针对物理教学中的数学技巧进行探究。
一、平抛运动概念
平抛运动属于生活中较为常见的一种物理运行形式,在高中物理教学中将其作为重点的曲线运行内容,属于重点学习内容,又是学生较难掌握的内容。人教版教材中将平抛运行定义为:当物体以一定的速度沿着水平方向抛出后,将空气的阻力忽略不计,物体仅承受来自自身的重力情况下,所产生的运行即可称之为平抛运动。通过分析可以发现,平抛运行实际上是由水平的匀速运行和竖直的自由落体运动共同组成。平抛运动的物体在运动的过程中会受到重力的影响发生速度的变化,因此,可以将平抛运动总结为是匀变速的曲线运动,而物体的运动轨迹为抛物线。
二、图像方程结合方法即数形结合法
在物理教学中,运动规律的学习离不开数学方法的支持。实际进行物理研究时,多采用数形结合的方式。在物理规律表现不明显的情况下,就需要数学数据做出辅助,为学生直观地展现变化规律,更便于他们理解和探究物理知识,为此,数学在实际教学活动中的应用较多[2]。数形结合指的是将数学语言用图形表现,通过数学语言和图形之间的相互转换作用,解释物理中的问题。主要形式有数转形、形转数和数形结合这三种。就平抛运动而言,教师可以在对平抛运行的实验数据进行分析之后,绘制出直角坐标系,利用数据标注出平抛物体的运动轨迹。通过这种方式,学生可以更直观地感受到平抛运动的运行规律。在对纵向坐标和横向坐标进行分析之后,可以得出平抛运动规律的方程。利用数据知识可以得出坐标系中的线为抛物线。因此,可以得出“平抛运动轨迹为抛物线 ”这一结论。同样,也可以用数学方程证明平抛运动轨迹为抛物线,由x=u0t,得因为是个定值,所以可以说明平抛运动轨迹为抛物线,如图1所示 。
此即数形结合方法的应用,为了培养学生的自主学习能力,可以将此种方式传授给学生。平抛运动无论是在高中物理教学中,还是在高考中都属于重点内容,但是平时教师对斜上抛运动的研究较少。实际上,两种运动轨迹可以采用同样的思路进行分析,但是数学方法相对较难,下面就做出具体分析。
三、运用数学技巧处理平抛运动的例题分析
如图2所示,从倾角为θ的斜面上以初速v0平抛一物体,不计空气阻力,经时间t,物体落在斜面上时其水平位移和竖直位移分别为x,y,则
遇到斜面上的平抛运动问题,往往会与这一关系式有关。所以,解题时要有意识地写出这一关系式。
例题:如图3所示,AB为斜面,BC为水平面,从A点以水平初速度v向右抛出一小球,其落点与A的水平距离为s1,从A点以水平初速度2v向右抛出一小球,其落点与A的水平距离为s2,不计空气阻力,s1∶s2可能为:______。
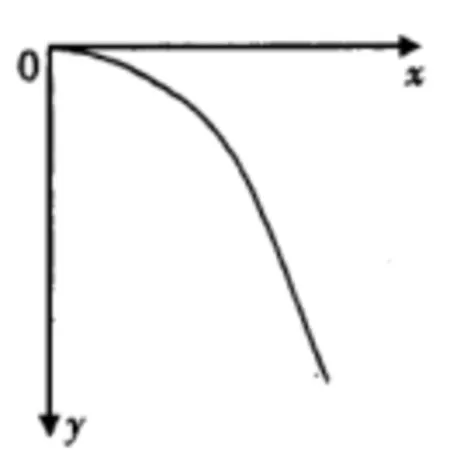
图1
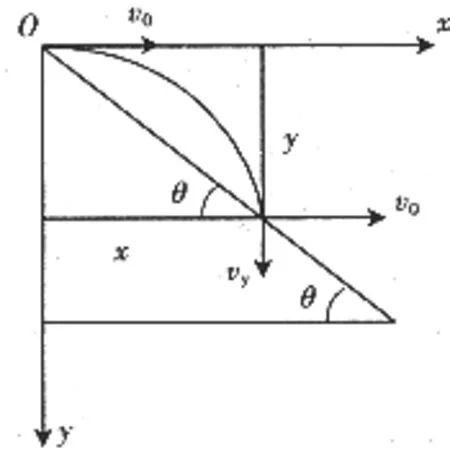
图2
A.1∶2 B.1∶3 C.1∶4 D.1∶5
解析:若两物体都落在水平面上,则运动时间相等,有s1∶s2=vt∶2vt=1∶2,A是可能的。
若第一球落在斜面上,第二球落在水平面上(图4),s1∶s2不会小于1∶4,但一定小于1∶2。
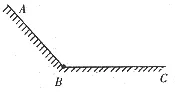
图3
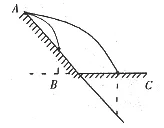
图4
故1∶3是可能的,1∶5不可能。
故s1∶s2可能为ABC。
结 语
斜上抛运动规律的分析相对于平抛运动而言,具有一定的难度。除了涉及物理内容之外,还涉及很多数学知识,如导数法求极值、利用参数方程求轨迹等,数学方法的应用可以加深学生对物理规律的理解和认识。可见,数学方法在物理规律中的有效应用,不仅能够实现学生对物理规律的探索,还能够提升学生的自主学习能力。
