应用圆的向量方程求向量模的最值

陈淑红 赵欣欣

(河北省定州中学 073000)

向量既有代数特征，又有几何意义，求向量模的最值问题往往需要公式分析出代数式的几何意义，利用几何图形求解.

预备公式1：已知平面向量a,b,如果向量c满足c-a=b，则向量c终点的轨迹是以a的终点为圆心,b为半径的圆.

预备公式2：如果非零向量a,b垂直，则a+b=a-b.

一、直接利用圆的向量方程求最值

例1 已知a,b是平面内两个互相垂直的单位向量，若c满足(a-c)·(b-c)=0，则c的最大值是( ).

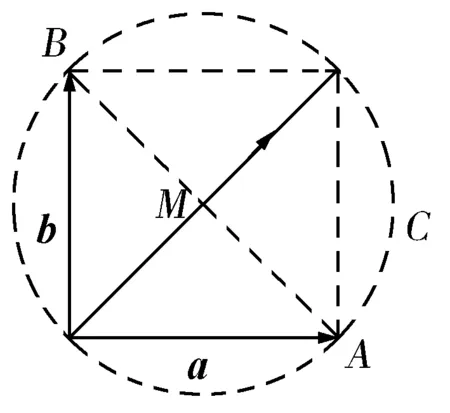
解因为(a-c)·(b-c)=0，所以(a-c)⊥(b-c).

由公式2得a-c+b-c=a-c-b+c,

即2c-a-b=a-b.

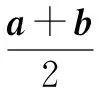
变式设a,b为单位向量，若向量c满足c-(a+b)=a-b,则c的最大值是( ).

解因为c-(a+b)=a-b,

则向量c终点的轨迹为以向量(a+b)的终点为圆心,以a-b为半径的圆,

另解可利用绝对值三角不等式得:

a-b=c-(a+b)≥c-a+b

所以c≤a-b+a+b.

二、构造圆求解最值

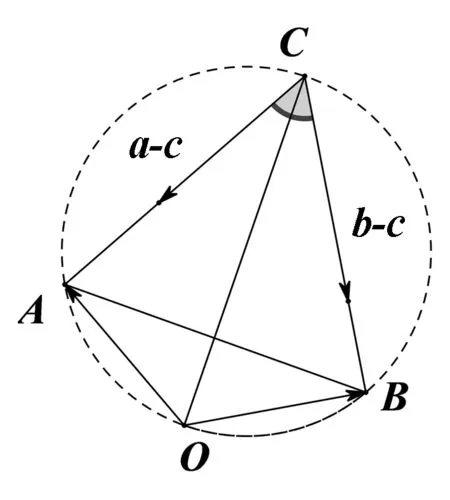
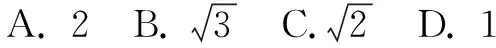
变式设向量a、b、c满足，a=b=1,〈a-c,b-c〉=60°,则c的最大值是( ).

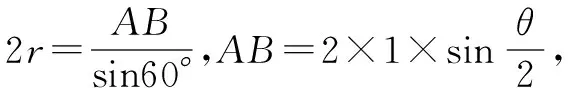
则cmax=OM+r.

设向量a与b夹角为θ

利用圆向量方程求解棱的最值问题，是利用向量表达式的几何意义画出相应圆的图形，转化为最值.这种方法是通法，简单易懂，能让学生更好的了解向量的本质.