高中数学中极值点偏移问题解法例析

何 静

(江苏省灌云县第一中学 222200)

一、极值点偏移类习题要有解题过程

虽然这个问题用高等数学来解是非常简单，但是苏教版数学教材中并未涉及此类问题，因此，在教学过程中，一些老师运用高等数学思想来解释问题，显然不符合高中数学的教学要求，这在一定程度上超出了学生的能力范围，但实质是导数的应用，呈现的形式往往非常简短，涉及函数的双零点是一个多元数学问题，无论结论是两个变量的不等式还是导数函数值的不等式，消元构造一元函数是解决多元问题的基本方法.

题源已知函数f(x)=x2-2x+3，如果x1、x2满足f(x1)=f(x2),探讨x1+x2与2的关系.

解法利用函数的单调性及二次函数的对称性，因为函数f(x)的图象关于x=1对称，所以f(x)=f(2-x)，又因为f(x1)=f(x2)，所以f(x1)=f(2-x1)=f(x2)，所以x1+x2=2.

评注：本题是利用两个变量的对称转化为一个变量问题，将变量整理到同一单调区间内，研究函数在该区间内的单调性.那么对于非二次函数或者没有对称性的函数呢？

二、极值点偏移类习题通法的探寻

引例已知函数f(x)=xe-x，如果x1≠x2,满足f(x1)=f(x2),求证：x1+x2>2.

那可不可以利用这种对称手法整理到同一个单调区间？事实是可以实施的.解法如下：

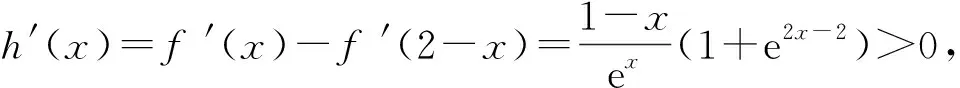
回顾解题过程，我们将会找到以下三个关键点，①x1和x2的范围；②不等式f(x)>f(2-x) ,x∈(1,+∞)；③把x2代入②式中的不等式，利用f(x)的单调性即可获证结论，以上三个关键点抓住了，就可以轻松解决一些极值点偏移问题.

三、极值点偏移类习题通法的延伸

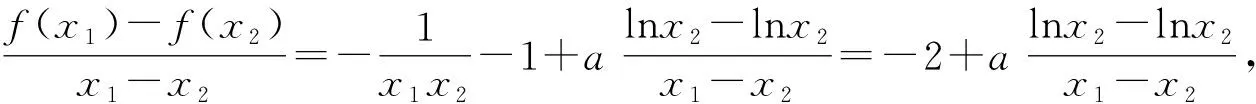
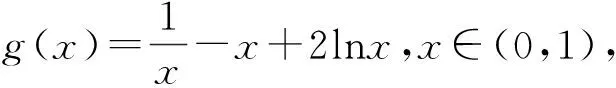
四、探询试题的解题规律

解法一是利用对称性(伪对称)可以用x1、x2的关系，将双变元的不等式转化为单变元不等式，构造新函数证明不等式，具体的操作如下三步：①求导f′(x)，获得f(x)的单调性、极值情况，作出f(x)的草图由f(x1)=f(x2)得x1、x2的取值范围；②设f(x)的极值点为x0，构造出新的函数F(x)=f(x)-f(2x0-x)或者F(x)=f(x0-x)-f(x0+x)，再求导F′(x)，利用零点x1(或者x2)得到的范围，来确定新函数值F(x)的正负;③代入x1或x2，并且利用f(x1)=f(x2)及极值点某一侧的单调性来证明即可.

事实上，让学生经历真实的提取有效信息、抽象建模的案例的学习是发展学生数学核心素养的重要载体，因此，我们更要关注学生对问题的深度理解，深度学习这是学生把知识转化为能力的必经之路.