多环过盈配合复合材料飞轮应力和位移分析

韩永杰，李 翀，王昊宇，任正义



多环过盈配合复合材料飞轮应力和位移分析

韩永杰，李 翀，王昊宇，任正义

（哈尔滨工程大学，黑龙江 哈尔滨 150001）

储能飞轮由轮毂和多环复合材料轮缘组成，飞轮旋转时轮毂和轮缘既受到离心力作用，同时又受到内外界面压力的作用，且不同转速下界面压力不断变化，使得分析计算由静止到最大工作转速的不同工况，以及飞轮上不同径向位置的应力非常复杂。本工作在平面应力下分别推导了各向异性材料轮缘在离心力作用下和受内外压力作用下的应力和位移解析式，进而采用叠加原理可计算飞轮在不同转速工况、径向不同位置的应力和位移，简化了应力和位移求解过程，可用于飞轮环间过盈量的确定、强度校核和极限转速计算等设计与分析。应用这种方法对一个实际飞轮进行了分析，并绘制了应力和位移曲线。

多环飞轮；复合材料飞轮；过盈配合；应力和位移

现代的飞轮储能为增加储能量和减小储能飞轮的质量，通常在高转速下工作。储能飞轮转速的提高又受到飞轮强度的限制，因此，采用高强度的复合材料飞轮成为现代储能飞轮的主要特征和标准配备。而复合材料为各向异性，使得飞轮的应力分布非常复杂[1]。

为了设计制造出安全可靠的高速储能飞轮，需要分析储能飞轮的应力和位移。目前的研究方法主要有解析法、数值方法和实验法[2]。解析法通常采用平面应力和平面应变的假设，易于建立起储能飞轮几何参数间的关系，更适合于储能飞轮的设计[3]。数值方法以有限元分析为主，可以进行三维应力和位移分析，需具体的飞轮几何尺寸后才能进行，适合于储能飞轮设计后的验证和进一步优化设计。实验法相对比较准确，但投资较大，适合于批量生产和工程化的储能飞轮以及较深入的理论研究。

在飞轮储能系统设计过程中，需要首先根据要求的储能量和工作转速，确定飞轮的转动惯量，然后确定储能飞轮的几何尺寸。目前的储能飞轮应力分析方法，计算过程较复杂，需要编制专用的程序或相应的软件才能完成，特别是在储能飞轮初步设计过程中应用不便。因此，本工作从实际工程应用的角度出发，分析了储能飞轮在离心力和环间装配压力作用下的应力和位移，可用于飞轮环间过盈量的确定、强度校核和极限转速计算等设计与分析。

1 复合材料飞轮受力分析

储能飞轮主要由轮毂和单环或多环复合材料轮缘组成[4]，如图1所示，图中1为轮毂，2、3、4为复合材料轮缘。轮毂与转子轴相连接，通常为金属材料。轮缘为高强度纤维复合材料，采用环向缠绕成型。轮毂与轮缘或各环轮缘之间为过盈配合，通常采用压力装配。

轮毂和轮缘受到装配界面压力作用、旋转时的离心力作用，以及温度变化引起的应力。因为前两项影响最大[5]，所以本工作未考虑温度变化引起的热应力影响。储能飞轮轮毂和轮缘中以多环中间轮缘最具代表性，为各向异性复合材料，既受到离心力的作用，又在内外界面上同时受到过盈配合压力的作用，轮毂的金属材料和单侧装配界面受到压力时只是其特例。因此，各向异性复合材料轮缘受到离心力作用、又受到内外表面压力作用的应力和 位移解析式成为分析和计算飞轮轮毂和各轮缘的关键。

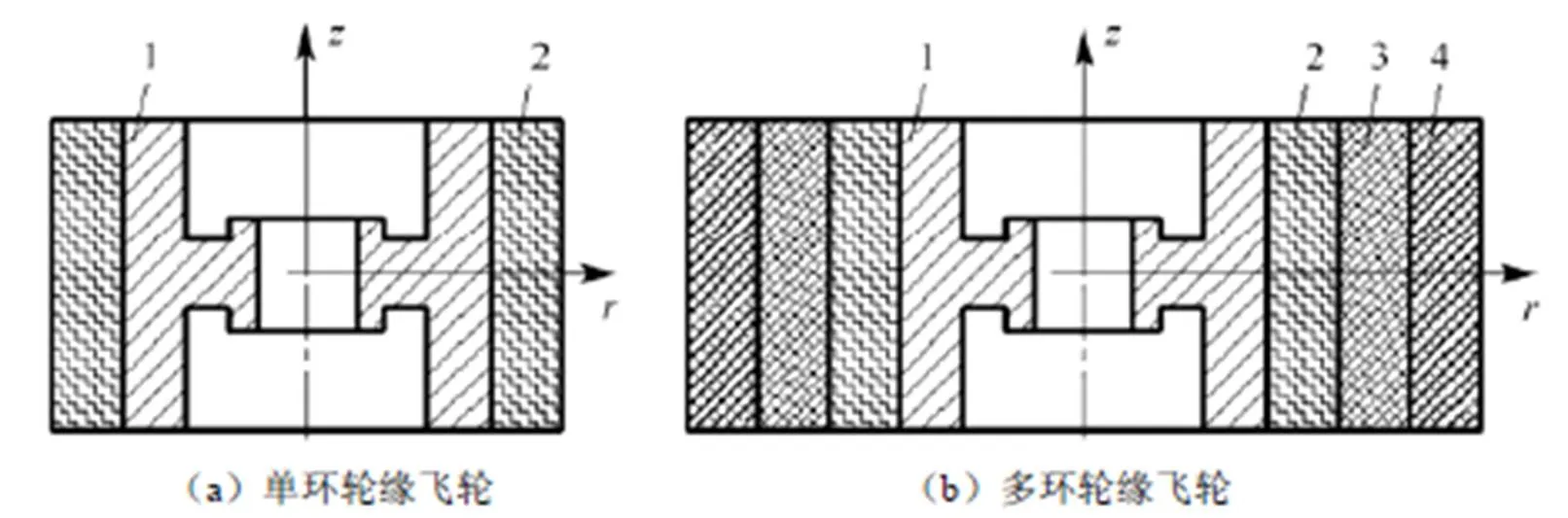
图1 复合材料飞轮的结构

2 力学方程的建立

2.1 柱坐标平衡方程和几何方程

如图1所示建立柱坐标系（、、），轴线为，半径方向为，旋转方向为。由于飞轮轮缘的几何形状、约束情况及所受的外力都对称于转子轴线，所以为空间轴对称问题。轴对称平面应力情况，体力为离心力的平衡方程[1]见式(1)

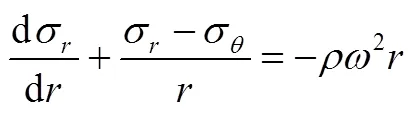
式中，为半径；σ为径向应力；σ为环向应力；为密度；为角速度。

轴对称平面应力情况，当无体力时，式(1)平衡方程右侧为零。由于为轴对称，所以只有径向位移，环向位移为零。柱坐标轴对称平面应力情况的应变-位移关系见式(2)

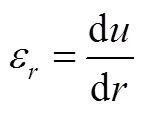
式中，ε为径向应变；为环向应变。

2.2 横向各向同性材料本构方程

复合材料轮缘一般由纤维环向缠绕制成，其在柱坐标下为正交各向异性材料。根据复合材料层压板理论，垂直于纤维的面为各向同性面，复合材料轮缘又为横向各向同性材料。柱坐标轴对称平面应力问题横向各向同性材料应力-应变关系[6]见式(3)

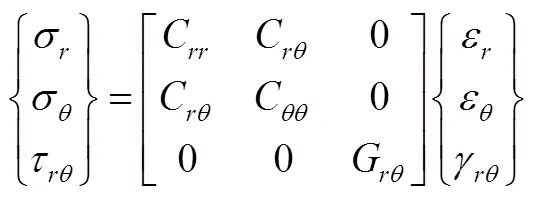
式中，C、C、C分别为应力-应变刚度系数，G为剪切弹性模量。刚度系数可用复合材料的工程弹性常数表示，具体见式(4)

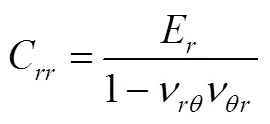
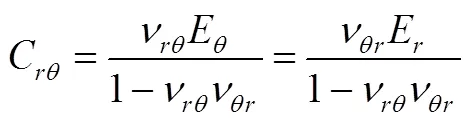
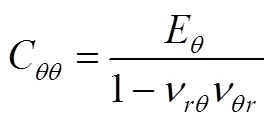
式中，为弹性模量，为泊松比，下标表示坐标方向。

2.3 横向各向同性材料位移微分方程

将式(2)代入式(3)得

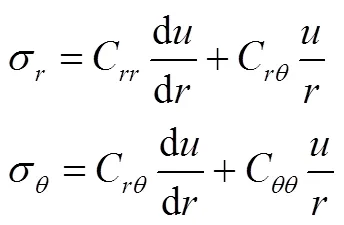
将式(5)代入式(1)并整理得式(6)

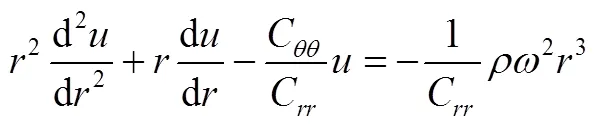
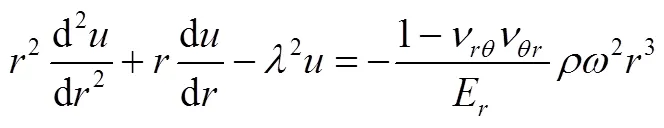
3 应力和位移解析式

3.1 径向位移微分方程的解

径向位移微分方程式(7)为变系数二阶欧拉型微分方程，它的解由式(8)齐次方程的通解式(9)和特解组成。

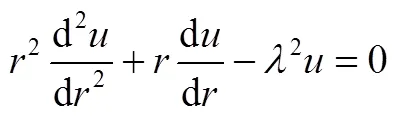
式中，1、2为系数，由边界条件确定。

由于=3不是特征方程的根，式(7)的解为

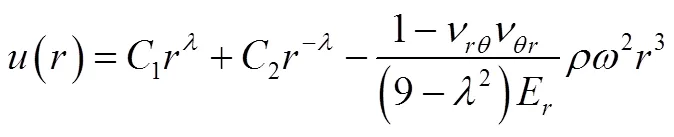
3.2 压力作用下应力和位移的解析式

在界面压力作用下无离心体力存在，则微分方程的解为上面齐次方程式(8)的通解式(9)。将式(4)和式(9)分别代入式(5)并整理得

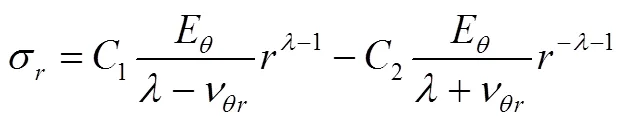
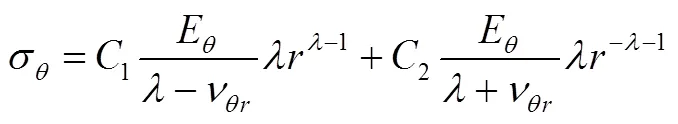
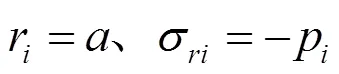
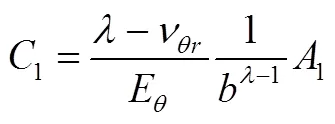
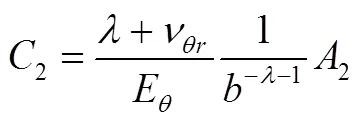
式中，

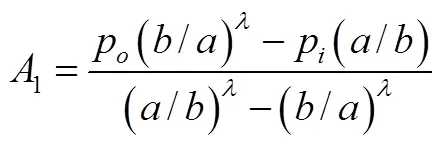
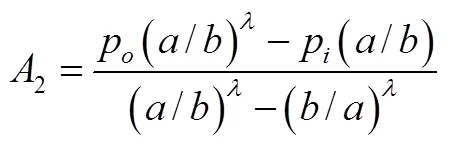
将系数1和2代入式(9)、式(11)、式(12)分别得在界面压力作用下的径向位移、径向应力和环向应力的解析式

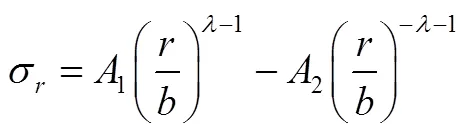
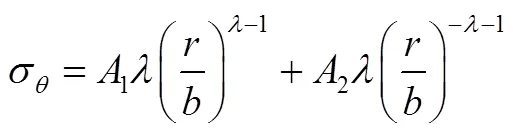
3.3 离心力作用下应力和位移的解析式

飞轮在离心力作用下应力和位移的计算和分析，关键是根据边界条件确定微分方程解中的系数。纯离心力作用下边界条件为径向内外压力为零，即无径向应力存在。将式(4)和式(10)分别代入式(5)并整理得

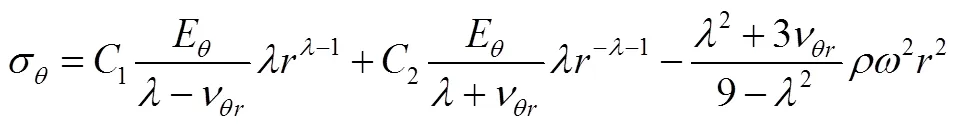
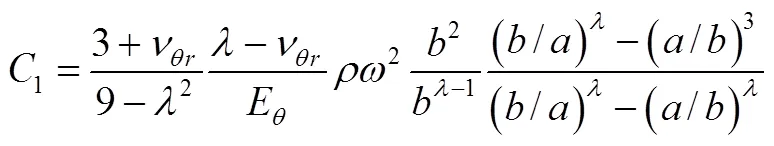
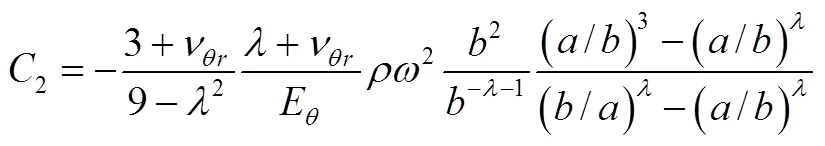
将式(22)、式(23)的系数分别代入式(20)、式(21)、式(10)得式(24)径向应力、式(25)环向应力、式(26)径向位移的解析式

式中，

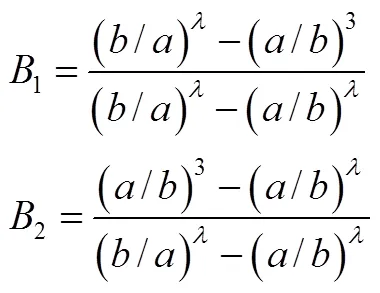
4 应用实例

根据上面推导的横向各向同性材料应力和位移解析式，分析计算600 W·h储能飞轮（图1为单环轮缘飞轮）的应力和位移，飞轮的材料性能参数见表1[7-8]。轮毂和轮缘采用压力过盈配合，安全运转时环间径向压力所产生的摩擦力不小于轮缘的重力，按此原则确定可保证两环不脱落。

表1 飞轮轮毂和轮缘材料性能参数

安全运转工况飞轮同时承受环间径向压力和离心力作用，飞轮不同半径处的径向应力分别由式(18)、式(24)计算，环向应力由式(19)、式(25)计算，径向位移由式(17)、式(26)计算，然后用叠加原理将相应半径处径向应力、环向应力和位移相加，可得到储能飞轮不同半径处的应力和位移曲线。图2为环间径向压力作用下径向应力分布曲线，图3为离心力作用下径向应力分布曲线，图4为安全运转工况径向应力分布曲线。图5为环间径向压力作用下环向应力分布曲线，图6为离心力作用下环向应力分布曲线，图7为安全运转工况环向应力分布曲线。图8为环间径向压力作用下径向位移曲线，图9为离心力作用下径向位移曲线，图10为安全运转工况径向位移曲线。

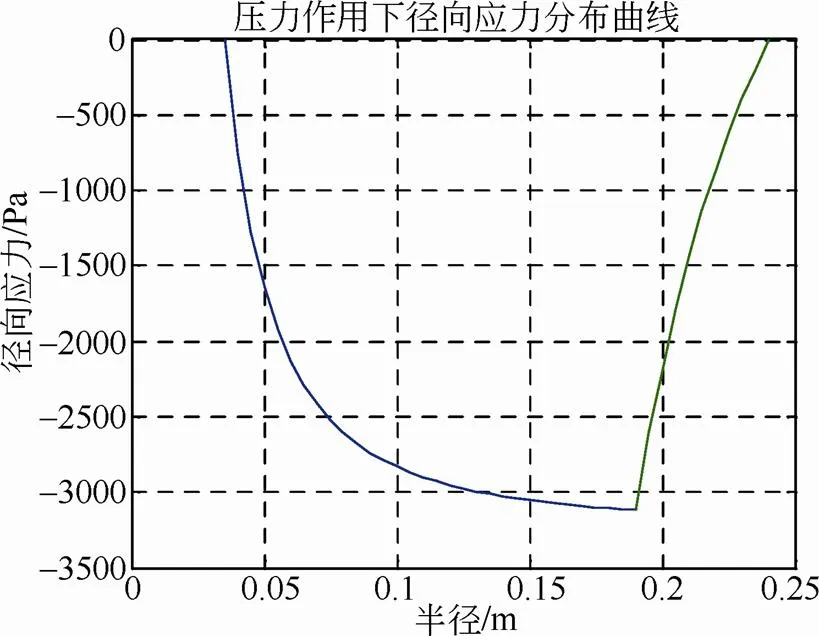
图2 压力作用下径向应力分布曲线

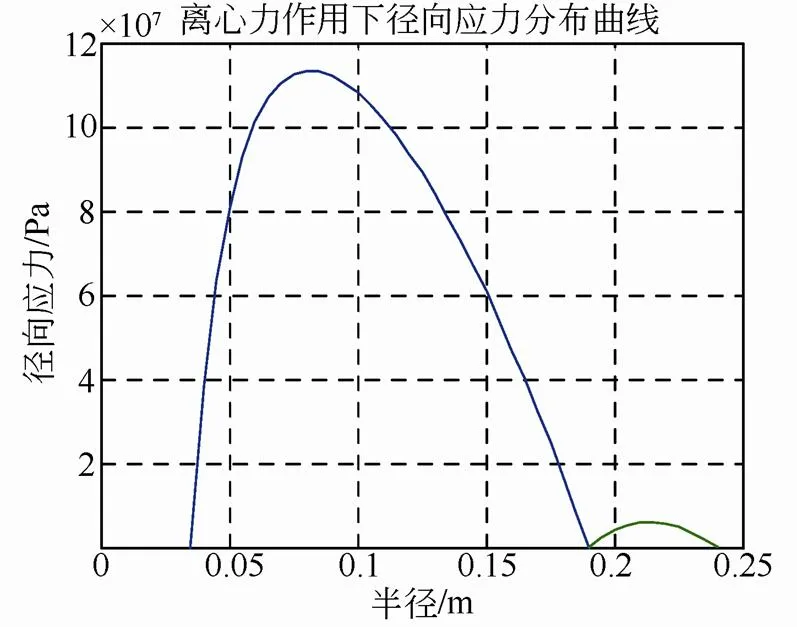
图3 离心力作用下径向应力分布曲线

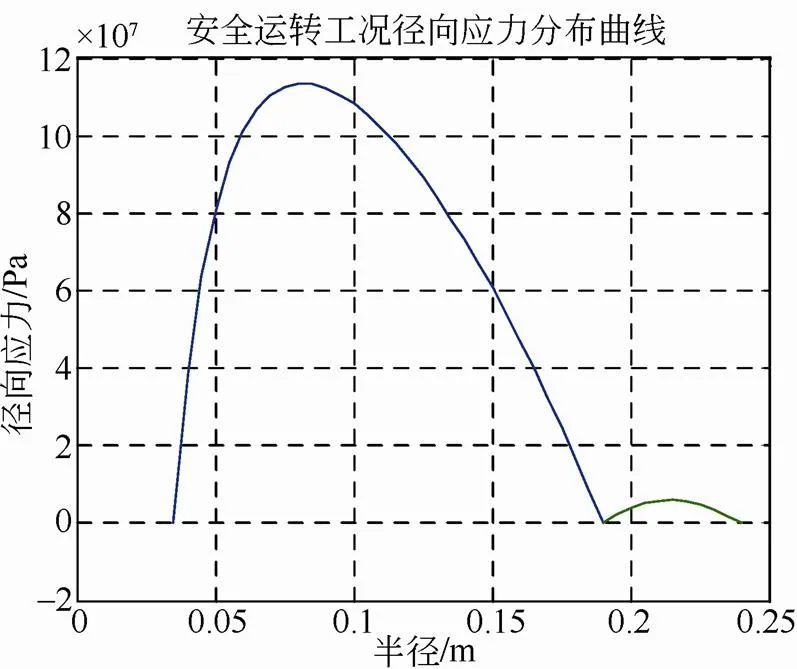
图4 安全运转工况径向应力分布曲线

图5 压力作用下环向应力分布曲线

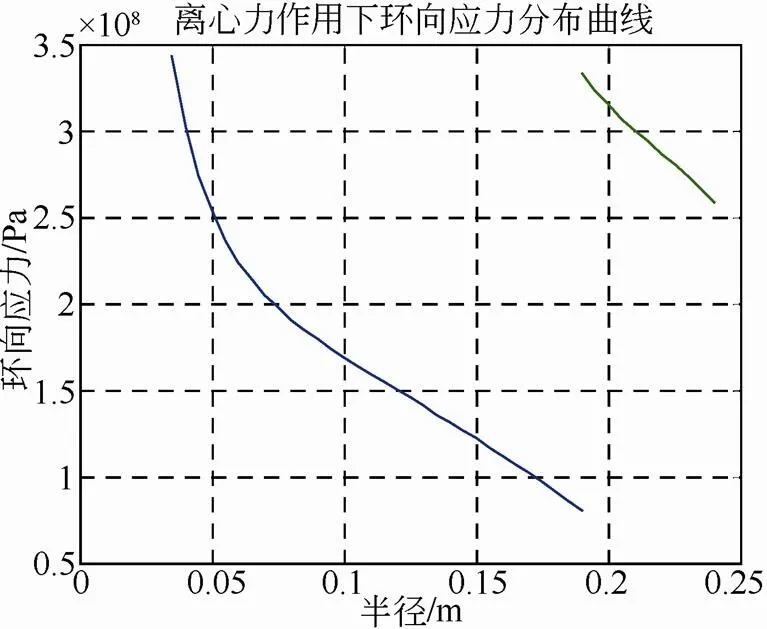
图6 离心力作用下环向应力分布曲线

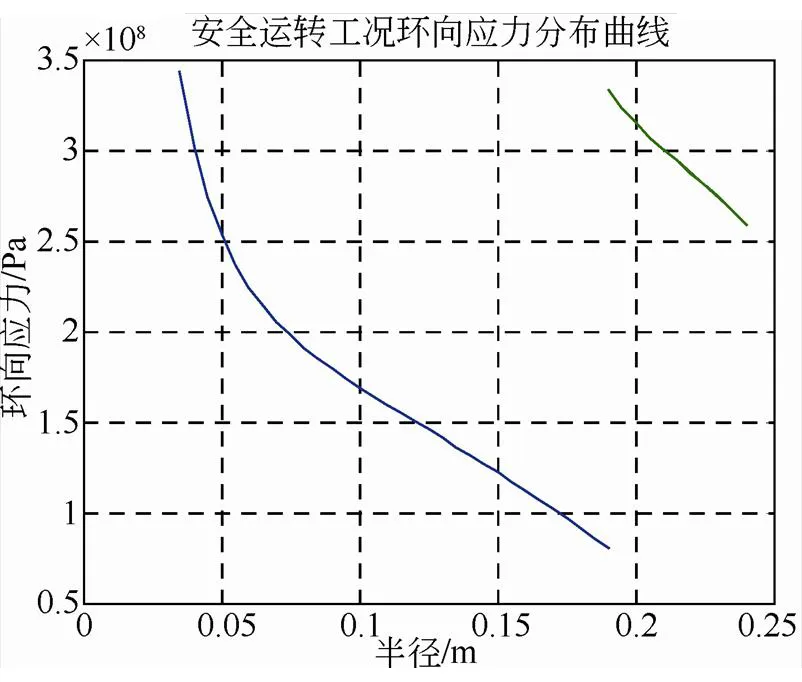
图7 安全运转工况环向应力分布曲线

由图中可以看出，图2在界面压力作用下径向应力为负值，与图3离心力作用下径向应力相比较小。图3金属轮毂径向应力远大于复合材料轮缘的径向应力，这与实际应用的材料强度是相符的，这是由于复合材料缠绕轮缘在径向的强度极限远低于环向。图4是图2和图3的叠加的结果，离心力引起的径向应力是主要的。图5、图6、图7为环向应力曲线。图8、图9、图10为径向位移曲线，从图中看在界面处位移不连续，主要原因是过盈装配后轮毂和轮缘有预变形，界面上相对位移还是相等。

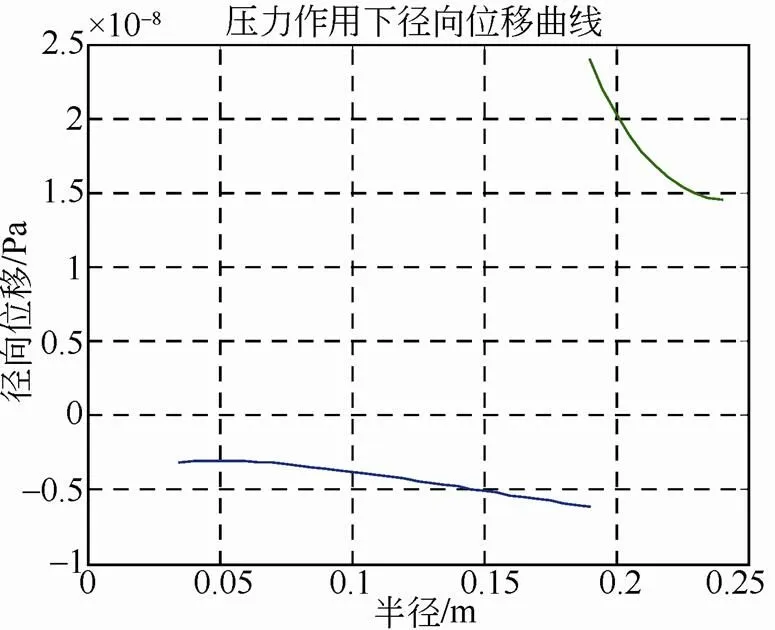
图8 压力作用下径向位移曲线

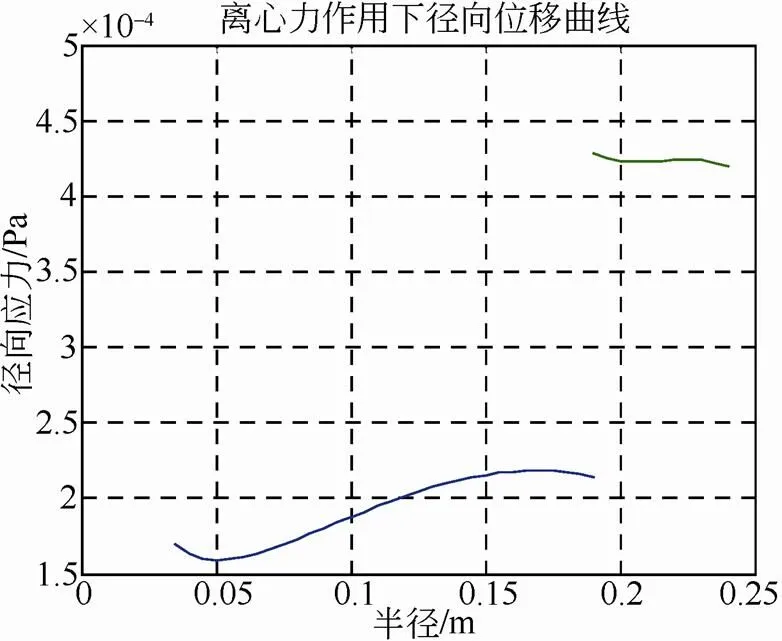
图9 离心力作用下径向位移曲线

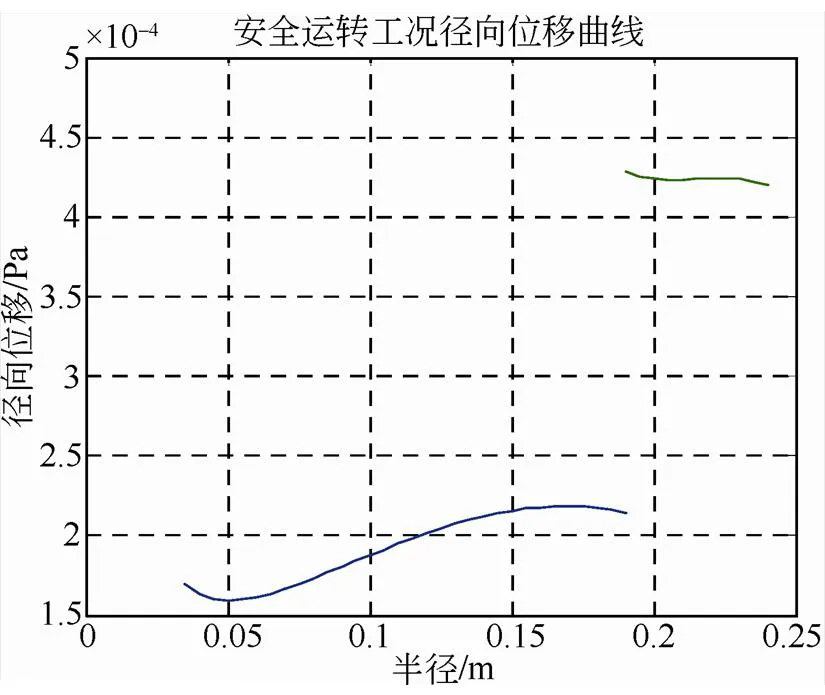
图10 安全运转工况径向位移曲线

5 结 论

在平面应力下推导了储能飞轮分别在压力和离心力作用下的应力和位移解析式，材料为横向各向同性材料，适用于金属轮毂和缠绕复合材料轮缘。可用于储能飞轮静止、加减速和安全运转各工况 应力和位移分析计算。并以600 W·h储能飞轮为例计算了应力和位移，并绘制了飞轮不同半径处的应力和位移曲线。通过上面的分析，可以得出如下 结论。

（1）横向各向同性材料的应力和位移解析式，适用于储能飞轮各环的分析计算。应用解析式可确定合理的环间过盈量和压力装配的压力等设计、制造参数。

（2）根据飞轮静止、加减速和安全转速不同工况的受力情况，应力和位移解析式均适用，对同时受两种力的状况，采用叠加原理。立轴储能飞轮安全运转工况的环间压力以外环重力为约束，更接近实际。

（3）从图中应力和位移曲线可知，复合材料在离心力作用下位移大于金属轮毂。在有环间径向压力作用下，径向应力为负值，可有效提高飞轮的 强度。

[1] HA S K, KIM S J, NASIR S U, et al. Design optimization and fabrication of a hybrid composite flywheel rotor[J]. Composite Structures, 2012, 94: 3290-3299.

[2] ARNOLD S M, SALEEB A F, Al-ZOUBI N R. Deformation and life analysis of composite flywheel disk systems[J]. Composites Part B, 2002, 33: 433-459.

[3] 李成, 常向前, 郑艳萍, 等. 复合材料储能飞轮应力位移场分析及与均质材料飞轮比较[J]. 太阳能学报, 2007, 28(10): 1168-1171.

LI C, CHANG X Q, ZHENG Y P, et al. Study on stress and displacement field of composite flywheel for energy storage[J]. Acta Energlae Solaris Sinica, 2007, 28(10): 1168-1171.

[4] 赵韩, 杨志轶. 复合材料飞轮的设计分析[J]. 机械强度, 2003, 25(2): 163-166.

ZHAO H, YANG Z Y. Design analysis of composite material flywheel[J]. Journal of Mechanical Strength, 2003, 25(2): 163-166.

[5] ASGHARI M, GHAFOORI E. A three-dimensional elasticity solution for functionally graded rotating disks[J]. Composite Structures, 2010, 92: 1092-1099.

[6] 赵美英, 陶梅贞. 复合材料结构力学与结构设计[M]. 西安: 西北工业大学出版社, 2007: 1-8.

ZHAO M Y, TAO M Z. Structural mechanics and structural design of composite materials[M]. Xi’an: Northwestern Polytechnical University Press, 2007: 1-8.

[7] HAN Yongjie, REN Zhengyi, TONG Yongxiang. General design method of flywheel rotor for energy storage system[J]. Energy Procedia, 2012, 16: 359-364.

[8] ARVIN A C, BAKIS C E. Optimal design of press-fitted filament wound composite flywheel rotors[J]. Composite Structures, 2006, 72: 47-57.

Analysis of the stresses and displacements for a composites interference fit multi-rim flywheel

HAN Yongjie,LI Chong, WANG Haoyu, REN Zhengyi

(Harbin Engineering University, Harbin 150001, Heilongjiang, China)

A flywheel stores energy was composed of hub and multi-rims made of filament winding with carbon fiber. The hub and rims were subject to axisymmetric centrifugal forces due to rotation and pressure come from the interface of rims. The interface pressure varying with the rotation speed made the stress analysis being very complexity at various radius and condition from stop to the maximal operation speed. In this investigation, based on the assumption of a plane stress, an analytic method for calculating the stresses and displacements distribution of the orthotropic rim is presented respectively. Moreover, the superposition principle was applied to calculate the stresses and displacements. The relatively simple solving process was applied to analyze and design the flywheel, such as choosing the interference fit, evaluating strength of the flywheel, and calculating the maximal speed. The analysis result of the stresses and displacements was carried out for an actual flywheel design example.

multi-rim flywheel; composites flywheel; interference fit; stress and displacement

10.12028/j.issn.2095-4239.2018.0011

TH 145.4；TH 131.7

A

2095-4239（2018）05-815-06

2018-01-22；

2018-04-18。

国家高技术研究发展计划（863计划）项目（2013AA050802），黑龙江省科技攻关计划项目（GZ11A208）。

韩永杰（1963—），男，高级工程师，研究方向为储能技术与应用、飞轮强度和转子动力学，E-mail：hanyongjie@hrbeu. edu.cn；

李翀，副教授，研究方向为储能技术与应用，复合材料设计与制造技术，E-mail：lichong@hrbeu.edu.cn。