考虑空气压缩因子变化影响的地下储气库热力学过程分析
2018-09-21蒋中明刘澧源梅松华
蒋中明,刘澧源,胡 炜,梅松华,李 鹏
考虑空气压缩因子变化影响的地下储气库热力学过程分析
蒋中明1,2,刘澧源1,胡 炜1,梅松华3,李 鹏3
(1长沙理工大学水利工程学院,湖南 长沙 410114;2水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114;3中国电建中南勘测设计研究院有限公司,湖南 长沙 410014)
为了解空气压缩因子变化对压气储能电站地下储气库热力学过程的影响,研究了考虑压缩因子变化条件下的压缩空气热力学过程的计算方法,利用实测数据论证了4种压缩因子计算方法的合理性,结合工程算例,研究了循环充放气状态下地下储气库压缩空气温度及压力变化规律。研究表明,空气压缩因子变化对压缩空气温度和压力计算值有显著影响;循环充放气条件下空气压缩因子、温度和压力均随充放气次数的增加呈现出增大趋势,并逐渐趋于稳定;压缩空气温度计算值对压缩因子的敏感程度大于压缩空气压力计算值。将压缩空气假定为理想气体对储气库温度的估计将产生较大影响,因此,考虑压缩因子的影响是必要的。
压气储能;地下储气库;热力学过程;压缩因子
压缩空气储能(compressed air energy storage,简称CAES)地下储气库内压缩空气压力和温度变化过程具有高度复杂性[1]。为了求解储气洞室内压缩空气的温度和压力,KUSHNIR等[2]通过建立压气储能洞室的热力学控制方程,运用无量纲因子推导了求解压缩空气温度和压力的解析解。MANDHAPATI等[3]研究了考虑压缩空气与围岩之间热量交换效应对压缩空气温度和压力估计的影响。由于压缩空气不是理想气体,KUSHNIR等[4]在计算中采用了SYCHEV[5]建议的压缩因子计算模型分析了空气压缩因子对计算结果的影响,结果表明压缩因子变化对压缩空气压力的估计有较大影响。
空气压缩因子与温度和压力同时相关,且空气压缩因子与温度和压力之间存在高度的非线性关系[6-7]。对于CAES地下储气库来说,由于考虑到存储的压缩空气体量庞大,压缩因子对CAES地下储气库压缩压缩空气热力过程分析的影响,还需要深入研究。为此,本文尝试研究压缩因子变化特性对CAES电站储气库压缩空气温度和压力的影响。
1 考虑压缩因子变化的压缩空气热力学模型
1.1 热力学控制方程
对于岩穴地下储气洞室,其容积通常为一常量。如果密封层气密性良好,储气库漏气量可以忽略不计。对此,KUSHNIR等[4]提出了储气库压缩空气的热力学控制方程如下




对于洞室中的气体焓和内能的表达,可以由下式替换

式中,C为空气等压比热容,J/(kg·K);i为注入的空气温度,K;0为洞室内气体的初始温度,K;0为洞室内气体的初始密度,kg/m3;为对的导数。
1.2 空气压缩因子对温度偏导数

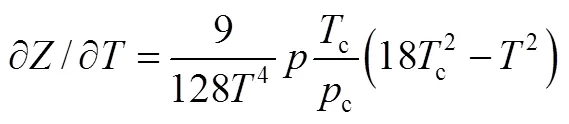
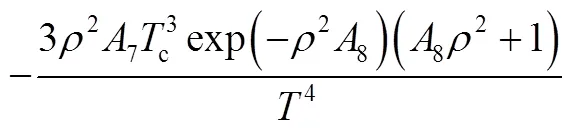

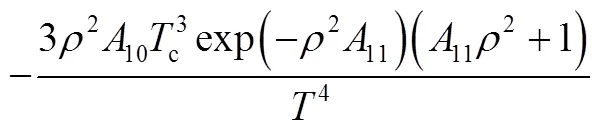


式(10)等号右边的各项偏导数如下

2 模型验证
压缩空气热力学模型可采用数值差分法进行求解[9]。本文利用FLAC3D平台的热传导分析功能求解式(2)中的对流换热项,储气库内压缩空气的热力学过程模型则采用FLAC3D平台中的FISH语言编程求解。模型验证算例采用Huntorf电站的实验数据,见表1。
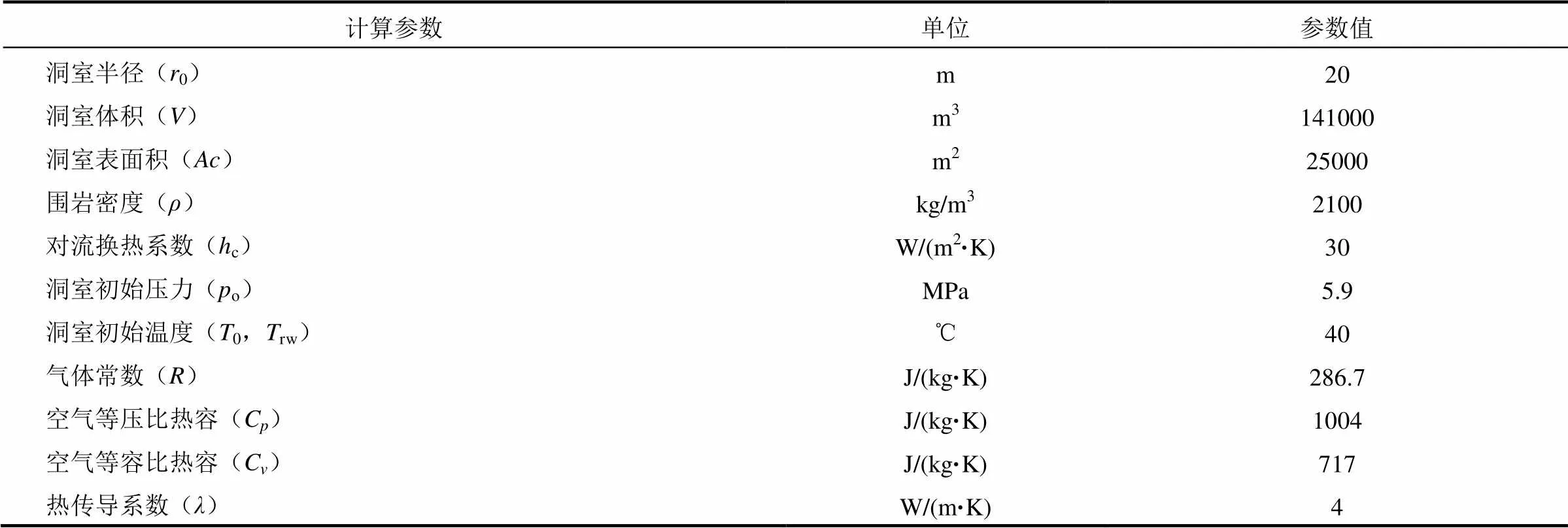
表1 Huntorf电站采用的计算参数[3]
Huntorf 电站在一个运行周期内的充放气速率见图1,三次注入的空气温度分别为50.96 ℃、 45.95 ℃和49.08 ℃。另外,为了简化计算,第一个小时内的放气速率取平均值-150 kg/s。
图2和图3分别给出了考虑空气压缩因子影响的压缩空气压力和温度的计算成果。由图可知,采用的压缩因子计算方法不同,计算得到的压缩空气压力和温度也存在一定的差异。其中,=1、BWRS方程、Berthelot方程以及DAK方程计算得到的压缩空气温度和压力结果与实测数据相差较小,而Brill&Beggs方程计算得到的压缩空气温度和压力结果与实测数据相差较大。

图1 Huntorf电站充放气速率[2]

图2 温度计算值与实测值对比

图3 压力计算值与实测值对比
表2和表3给出了考虑压缩因子的不同计算方法得到的温度和压力计算值与实测数据的对比。压缩空气温度和压力的计算值与实测值的均方根误差可由下式计算

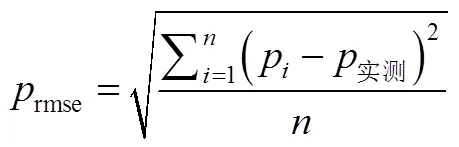
计算得到的均方根误差如表2和表3所示。由表2和表3可知,当=1时,计算得到的压缩空气温度和压力与实测数据之间的均方根误差最小,分别为rmse=1.299和rmse=0.079;采用4种压缩因子计算方法得到的压缩空气温度和压力均比=1时误差要大,其中,Brill&Beggs方法计算得到的压缩空气温度均方根误差最大,rmse=7.304,而DAK方法计算得到的压缩空气压力均方根误差最大,rmse=0.304。
在4种压缩因子计算方法的计算结果中,采用BWRS方法与Berthelot方法得到的计算误差相对较小,故下文分析中压缩因子采用Berthelot方法进行计算。采用Brill&Beggs方法与DAK方法得到的计算误差较大,在实际工程应用中不宜采用。
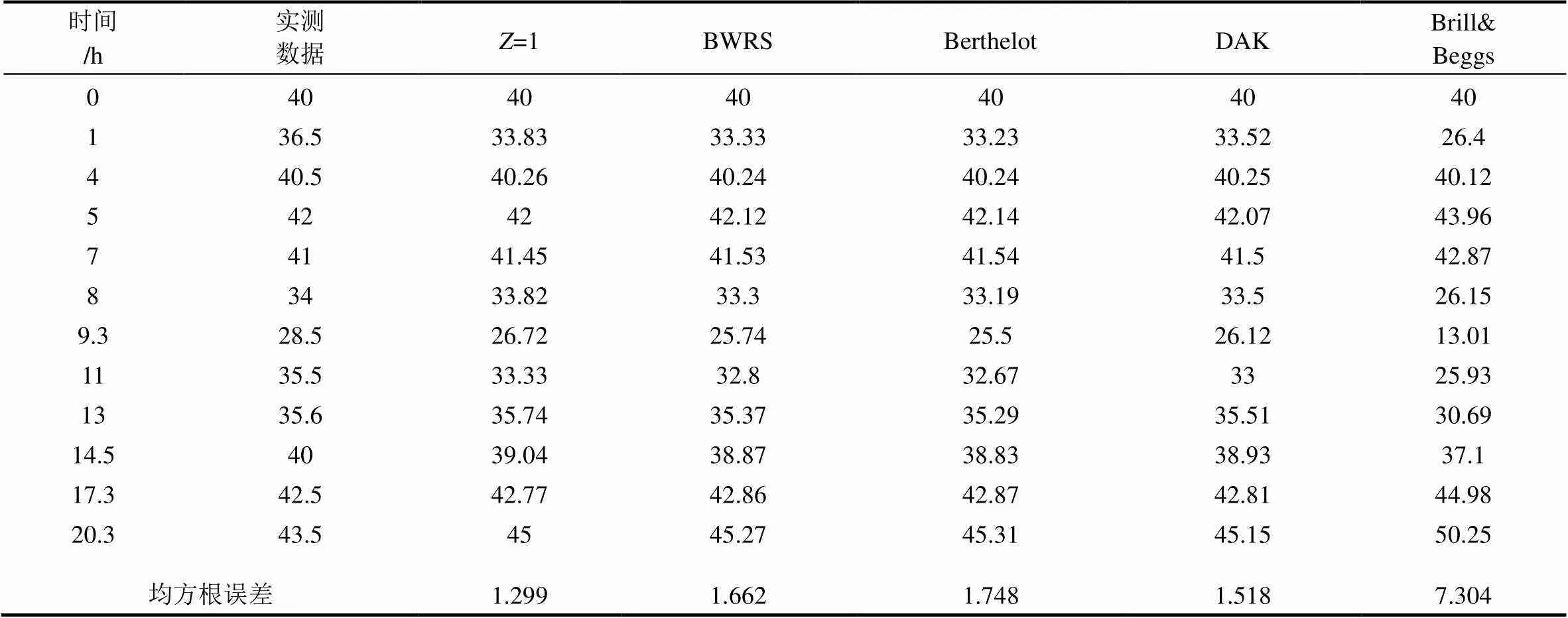
表2 温度计算值与实测值对比
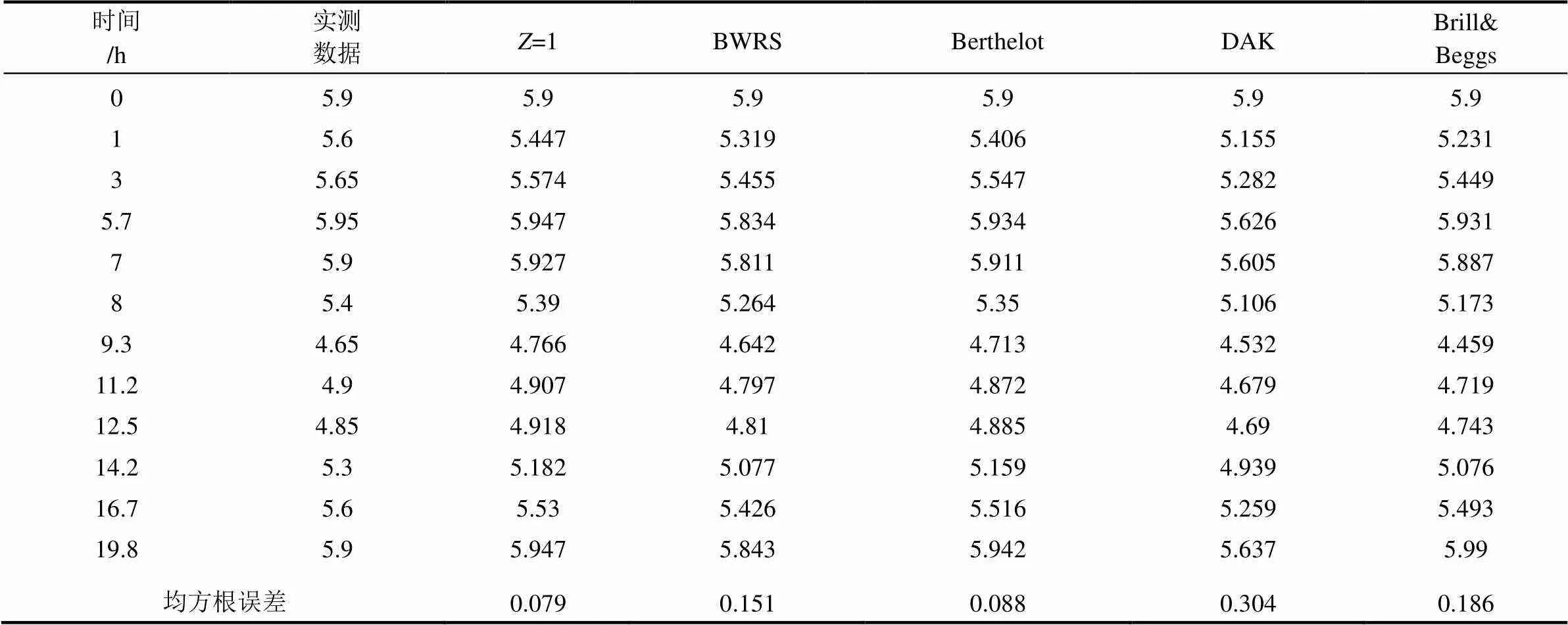
表3 压力计算值与实测值对比
3 循环充放气条件下压缩空气温度与压力变化过程分析
采用文献[10]给出的算例,研究运行工况条件下压缩空气的温度与压力变化过程。模型计算参数如表4所示。

表4 模型采用的计算参数
三维数值分析成果[11]表明:试验库储气室内的压缩空气蕴含的热量向储气室洞周围岩各个方向的传热过程基本一致。为简化计算,热传导分析的数值模型采用一维传热模型进行模拟。洞壁处为对流换热边界,远端岩体边界为固定温度边界,模型上下及前后边界面为绝热边界。
储气库循环工作的一个完整周期为:充气压缩→高压气体储存→放气发电→低压气体储存;每个阶段的工作时间为:8 h→4 h→4 h→8 h。运行周期:100天。
3.1 压缩因子的变化规律
图4给出了采用Berthelot方程计算得到的压缩因子在100个充放气循环过程中的变化规律。由图4可以看出,在100个充放气循环中,压缩因子计算值呈现逐渐增大的趋势,增大趋势随充放气次数的增加渐渐趋于平缓。由此可以看出,压缩因子随着充放气循环次数的增加进行会慢慢增大。压缩因子变化的变化趋势与温度的变化趋势(图5)基本保持一致,这是因为在计算公式中温度变化对空气压缩因子的影响占主导地位。
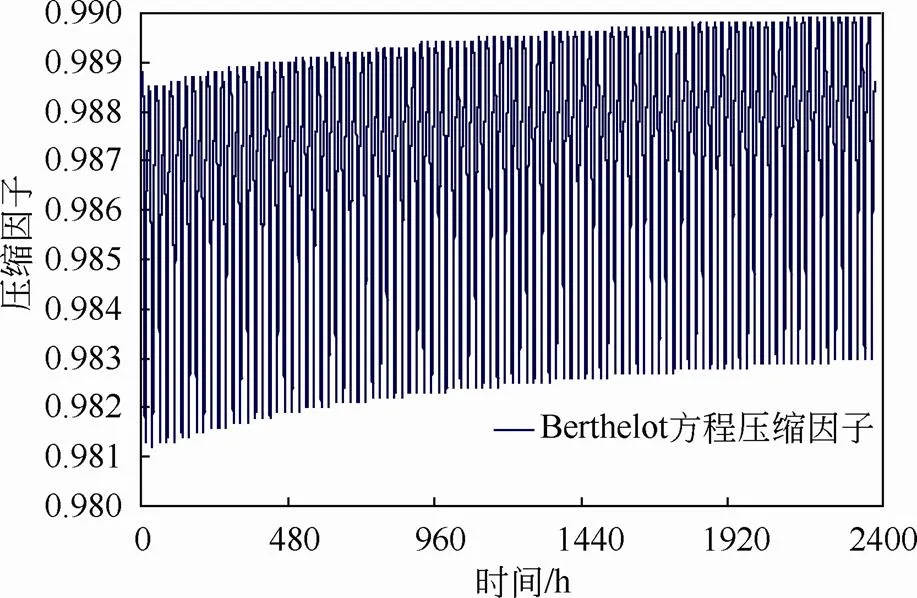
图4 压缩因子变化规律
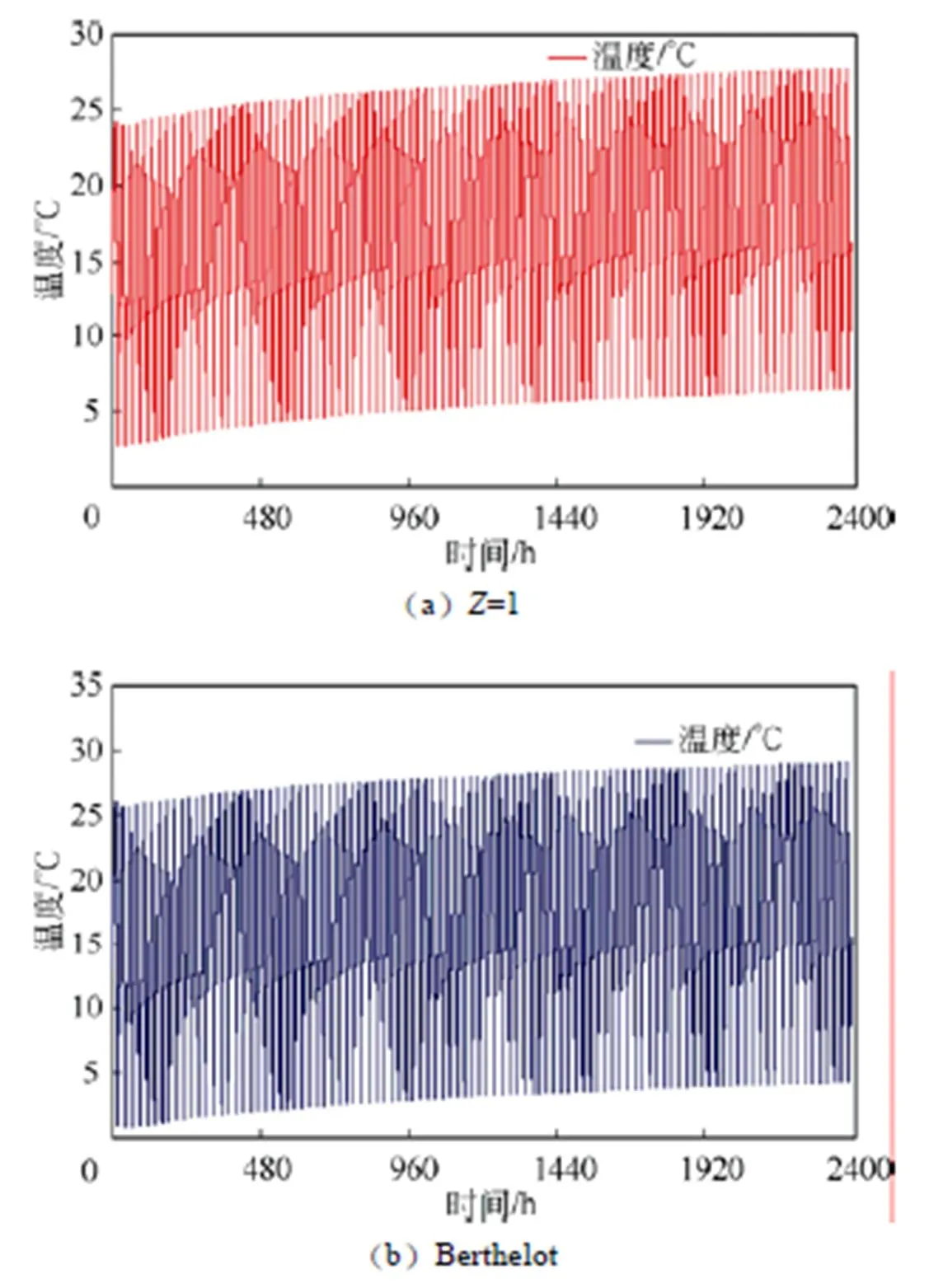
图5 压缩气体温度变化规律
3.2 储气库温度和压力变化规律
图5给出了=1和采用Berthelot方程时,计算得到的压缩空气温度在100个充放气循环过程中的变化规律。图5(a)中,压缩空气的温度随充放气循环次数的增加逐渐上升,上升趋势在后期趋于平缓。经过100个充放气循环后,空气温度极大值从24.2 ℃上升到27.7 ℃,升高了3.5 ℃,增加幅度约为14.5%;极小值从2.72 ℃上升到6.48 ℃,升高了3.76 ℃,增加幅度约为138.2%;一个充放气循环中最大温差由21.47 ℃增大到24.26 ℃。
图5(b)中,压缩空气温度变化幅度较图5(a)稍大:100个充气循环后压缩空气温度极大值比不考虑压缩因子影响时高1.4 ℃,压缩空气温度极小值比不考虑压缩因子影响时低1.81 ℃。经过100个充放气循环后,空气温度极大值从26.1 ℃上升到29.1 ℃,升高了3.0 ℃,增加幅度约为11.5%;极小值从0.91 ℃上升到4.30 ℃,升高了3.39 ℃,增加幅度约为372.5%;一个循环中最大温差由25.15 ℃降低为24.75 ℃。
由此可见,不考虑压缩因子影响将对压缩空气温度的预测影响产生相对较大误差(超过10%)。温度对密封层应力状态的影响显著,从而影响对密封层开裂与否的判断结论。因此,储气库压缩空气热力学状态的分析有必要考虑压缩因子的影响。
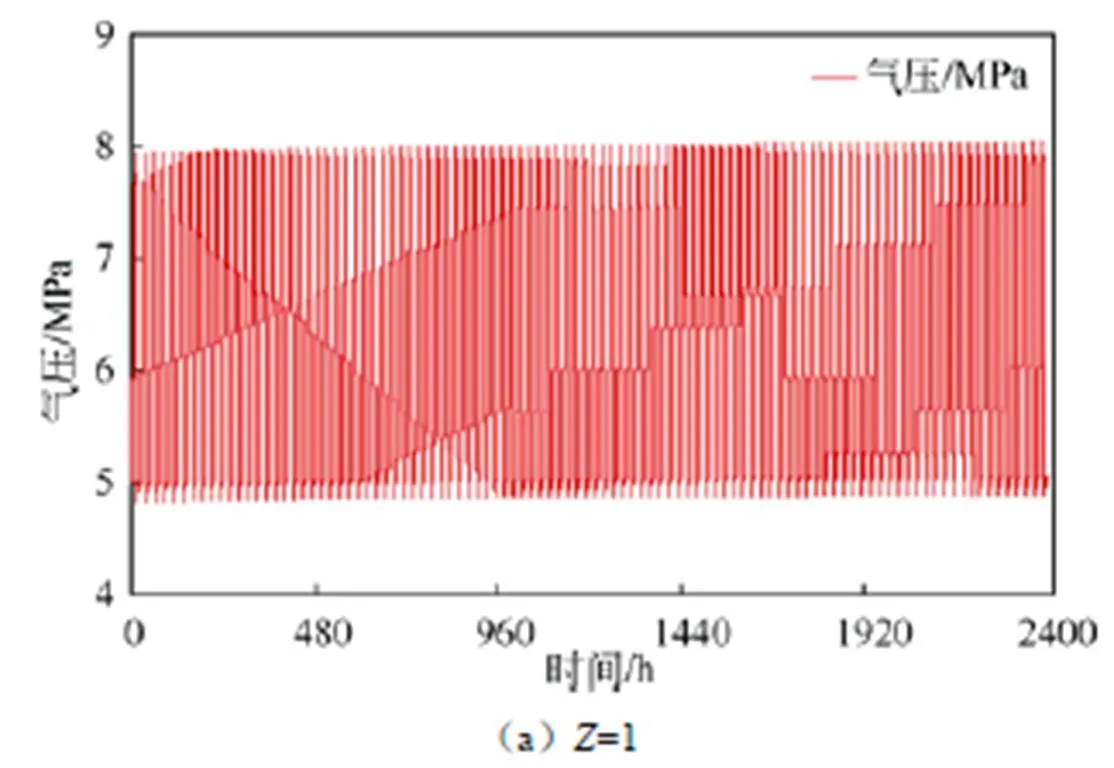
图6给出了=1和采用Berthelot方程计算得到的压缩空气压力在100个充放气循环过程中的变化规律。图6(a)中,空气压力随充放气次数的增加变化相对较小,经过100个充放气循环后,压缩空气压力极大值从7.946 MPa上升到8.041 MPa,升高了 0.095 MPa,增加幅度约为1.2%;极小值从4.82 MPa上升到4.886 MPa,升高了0.066 MPa,增加幅度约为0.8%;一个充放气循环中最大压力差由3.126 MPa增大到3.155 MPa,增大了0.029 MPa。后期压力的增加主要与压缩空气温度的升高有关。
图6(b)表明,考虑压缩因子影响情况下压缩空气压力极大值为7.994 MPa,比不考虑压缩因子影响时的8.041 MPa降低了0.047 MPa,降低幅度约0.6%。由此可见,压缩因子对压缩空气压力变化的预测影响相对较小。
4 讨 论
由于理想气体忽略气体分子本身的体积和分子间的作用力,故实际气体性质相对于理想气体性质会有所偏差,偏离程度取决于气体本身的性质以及温度、压强等因素。压缩因子的大小反映出真实气体对理想气体的偏差,同时可以反映出真实气体压缩的难易程度。对于理想气体,在任何温度压力之下,=1;当<1时,说明真实气体的体积比同样条件下理想气体的体积小,此时真实气体比理想气体易于压缩;当>1时,说明真实气体的体积比同样条件下理想气体的体积大,因此真实气体比理想气体难于压缩。
在充放气循环过程中,压缩空气温度的极大值与极小值会随着时间的变化而升高,升高趋势随充放气次数增加逐渐变缓。这是因为在长时间的循环工作条件下,由于围岩的热传导作用,压缩空气的热量由洞壁向围岩传递,热量累积使储气库围岩温度升高,进而导致压缩空气的温度进一步升高,而围岩温度不可能无限制地增大,故压缩空气温度升高趋势随时间渐缓。
5 结 论
研究了空气压缩因子变化对储气库热力学过程计算结果的影响,探索了地下储气库在频繁充放气循环条件下压缩空气温度和压力的变化规律。
(1)压缩因子变化对储气库内压缩空气温度和压力均有显著影响;空气压缩因子的计算方法不同,计算得到的空气温度和压力值差异较大。
(2)充放气循环条件下,压缩因子随充放气次数的增加呈现出逐渐增大的变化趋势,且在后期增大趋势趋于平缓。压缩空气的温度随充放气次数的增加也呈现明显升高的变化趋势,后期温度上升趋势也趋于平缓。
(3)在实际工程应用中,将压缩空气假定为理想气体对储气库温度应力的估计将产生较大影响,因此,考虑压缩因子的影响是必要的。
[1] KUSHNIR R, ULLMANN A, DAYAN A. Thermodynamic and hydrodynamic response of compressed air energy storage reservoirs: A review[J]. Rev. Chem. Eng., 2012, 28: 123-148.
[2] KUSHNIR R, DAYAN A, ULLMANN A. Temperature and pressure variations within compressed air energy storage caverns[J]. International Journal of Heat and Mass Transfer, 2012, 55(21/22): 5616-5630.
[3] MANDHAPATI R, SIDDHARTHA K K. Modeling and simulation of compressed air storage in caverns: A case study of the Huntorf plant[J]. Applied Energy, 2012, 89(1): 474-481
[4] KUSHNIR R, ULLMANN A, DAYAN A. Thermodynamic models for the temperature and pressure variations within adiabatic caverns of compressed air energy storage plants[J]. Journal of Energy Resources Technology, 2012, 134: 1-10
[5] SYCHEV V V, VASSERMAN A A, KOZLOV A D, et al. Thermodynamic properties of air[M]. Washington: Hemisphere, 1987.
[6] 刘毅, 周绍骑, 韩开进, 等. 基于BWRS方程的压缩空气压缩因子计算[J]. 后勤工程学院学报, 2014, 30(4): 66-71.
LIU Yi, ZHOU Shaoqi, HAN Kaijin, et al. Compressibility factor calculation method of compressed air based on BWRS equation[J]. Journal of Logistical Engineering University, 2014, 30(4): 66-71.
[7] YAN K L, LIU H, SUN C Y, et al. Measurement and calculation of gas compressibility factor for condensate gas and natural gas under pressure up to 116 MPa[J]. Journal of Chemical Thermodynamics, 2013, 63: 38-43.
[8] 陈剑文, 蒋卫东, 杨春和, 等. 储气库注、采气过程热工分析研究[J]. 岩石力学与工程学报, 2007, 26(S1): 2887-2894.
CHEN Jianwen, JIANG Weidong, YANG Chunhe, et al. Study on engineering thermal analysis of gas storage in slat formation during gas injection and production[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 2887-2894.
[9] 刘澧源, 蒋中明, 王江营, 等. 压气储能电站地下储气库之压缩空气热力学过程分析[J]. 储能科学与技术, 2018, 7(2): 232-239.
LIU Liyuan, JIANG Zhongming, WANG Jiangying, et al. Thermodynamic analysis of compressed air energy storage in a underground rock cavern[J]. Energy Storage Science and Technology, 2018, 7(2): 232-239.
[10] 周瑜,夏才初,赵海斌,等. 压气储能内衬洞室的空气泄漏率及围岩力学响应估算方法[J]. 岩石力学与工程学报, 2017(2): 297-309.
ZHOU Yu, XIA Caichu, ZHAO Haibin, et al. A method for the estimation of air leakage through inner seals and mechanical responses of the surrounding rock of lined rock caverns(LRCs) for compressed air energy storage[J]. Chinese Journal of Rock Mechanics and Engineering, 2017(2): 297-309.
[11] 蒋中明, 刘澧源, 李双龙, 等. 压气储能平江试验库受力特性数值研究[J]. 长沙理工大学学报(自然科学版), 2017(4): 62-68.
JIANG Zhongming, LIU Liyuan, LI Shuanglong, et al. Numerical study on mechanical characteristics of the Pingjiang pilot cavern for compressed air energy storage[J]. Journal of Changsha University of Science & Technology(Natural Science), 2017(4): 62-68.
Thermodynamic analysis of compressed air storage in a underground rock cavern considering the influence of compression factor
JIANG Zhongming1,2, LIU Liyuan1, HU Wei1, MEI Songhua3, LI Peng3
(1School of Hydraulic Engineering, Changsha University of Science & Technology, Changsha 410114, Hunan, China;2Key Laboratory of Water-Sediment Sciences and Water Disaster prevention of Hunan Province, Changsha 410114, Hunan, China;3PowerChina Zhongnan Engineering Corporation Limited, Changsha 410014, Hunan, China)
Thermodynamic analyses are performed to investigate the influence of varying air compression factor on compressed air storage in a underground rock cavern. Experimental data are used to validate four compression factor calculation methods. The results indicate that the temperature and pressure of compressed air are significantly influenced by the variation of the compression factor. Under cyclic charging and discharging processes, the compression factor, the temperature and the pressure of compressed air increase with increasing charging and discharging times, and eventually show a stablised trend. The calculated compressed air temperature is more sensitive than that of compressed air pressure when the compression factor is considered. The ideal gas assumption can lead to a large errors.
compressed air energy storage; underground rock cavern; thermodynamic process; compression factor
10.12028/j.issn.2095-4239.2018.0041
TU 311.3
A
2095-4239(2018)05-902-06
2018-03-22;
2018-06-25。
国家自然科学基金项目(51778070),中国电力建设集团科技计划项目(GW-KJ-2012-26)。
蒋中明(1969—),男,教授,主要从事能源地下存储与开发方面的科研工作,E-mail:zzmmjiang@163.com。
