基于GARCH-VaR方法的套期保值比率与效率的实证
2018-09-21曹志鹏
曹志鹏,路 华
(陕西科技大学 经济与管理学院,西安 710021)
0 引言
外汇套期保值通常是指以涉及两种或以上货币的商品或资本交易的实物交易为基础,在相关货币的衍生金融工具市场上进行与商品或实物交易中的货币流向相反,金额、期限、币种相同的交易。通过预先锁定成本或利用市场间的损益对冲来规避汇率波动所带来的外汇风险[1]。伍友韬(2017)[2]利用Copula函数的秩相关系数,并用t-GARCH模型建立最小方差套期保值模型,发现运用尾部相关系数计算得出的外汇最优套期保值率,能让套期保值后的收益率序列具有更小的均值和方差。彭红枫和陈奕(2015)[3]研究发现在套期保值模型中GARCH方法存在波动率的高持续性,这影响了对于资产价格序列描述的准确性,提出将MRS模型与GARCH模型相结合,以提高最优套期保值比率和效率。韩萍(2016)[4]构建金融衍生品的ECM-BGARCH模型来估算其套期保值效率,研究发现ECM-BGARCH模型可以优化套期保值比率,提高套期保值效率。唐韬和谢赤(2015)[5]提出了将状态转换动态Gaussian Copula模型来管理外汇风险,同时与OLS、DCC-GARCH、DCC-GaussianCopula等模型的套期保值效率进行比较。研究表明所构建的模型优于其他模型,利用该策略模型能有效规避外汇风险。本文在上述文献研究的基础上,构建以二元GARCH方法的VaR最优动态套期保值模型,并以静态模型作对比,以期找到企业管理外汇风险的最优方法。
1 模型构建
作为风险度量工具的VaR,可以用在企业外汇的风险管理中,使用VaR作为最小风险套期保值或均值方差套期保值比率中的目标函数。
已知对于收益率服从均值为E(Rh)、方差为的正态分布的套期保值资产组合,对于给定置信度a对应的收益单位时间的绝对VaR值为:

将 E(Rh)=E(Rs)-hE(Rf)式(1)得:

为使VaR最小,用VaR关于h求一阶导数,并令导数为零,整理得:

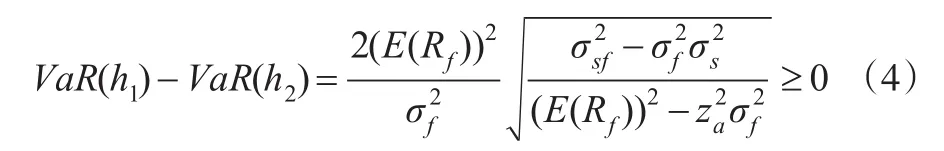
求解式(3)得到h1、h2。进一步验证哪一个是所要求的最优套期保值比率,分别代入绝对VaR的计算公式,并比较大小,简化得到:所以基于最小VaR的最优套期保值比率h=h2,因为σsf=ρσsσf,化简得到收益率服从均值为E(Rh)、方差为的正态分布的套期保值资产组合在置信度α下的最优套期保值比率:
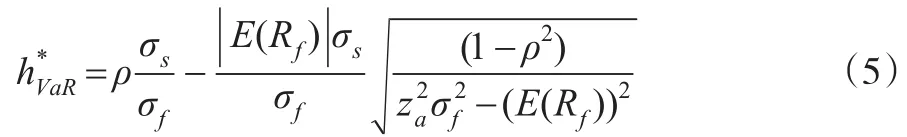
式(5)同时反映了投机需求和套期保值。第一部分ρσs/σf,是最小方差套期比,反映套期保值,不过没有体现套期保值者的风险偏好策。第二部分反映的是投机需求,体现了操作者对套期保值策略的风险偏好,本质上是投机期货。这一部分通过对置信水平α选取来反映套期者对风险的态度变化,置信水平α越大,套期保值者就越厌恶风险。
由于金融资产的波动存在异方差的特性,为了有效描述这一性质,文中引入GARCH(1,1)模型计算VaR的最优套期比率中的方差、协方差。
一个完整的残差向量和协方差矩阵滞后一阶的二元GARCH(1,1),即BEKK(1,1,k)的协方差矩阵方程为:
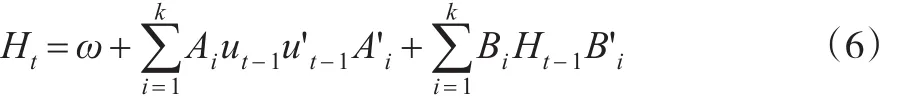
其中,ω是对称的二阶矩阵,Ai、Bi是二阶矩阵,k是BEKK方法的一个参数。在实际计算中可以设Ai、Bi为对角阵,取k=1,则模型简化为对角BEKK方法:
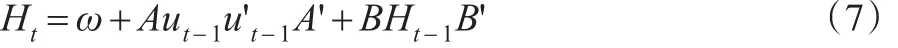
2 实证分析
2.1 数据选取
由于国内人民币衍生产品处在发展阶段,人民币远期、掉期的价格形成机制尚未完善,因此本文在实证分析中,选取境外的人民币无本金交割远期为标的。相比较其他境外人民币衍生品,无本金交割远期结售汇出现最早,交易也最活跃。文中数据选择期限为3月(M3)、6月(M6)两种人民币无本金交割远期合约的每日报价,时间跨度为2014年7月至2017年2月,以及同时期的人民币/美元每日即期汇率(CU)。除去各种因素每种合约有600个样本,数据来源于Wind咨讯。
为了计算最优套期保值比率,需要对汇率进行的一阶对数差分处理,得到3月期远期汇率、6月期远期和即期汇率三种数据的几何收益率,几何收益率曲线由于篇幅原因,本文不再赘述。从三个变量的几何收益率曲线可以发现,波动存在明显的时变性,初步判断这三个变量均具有条件异方差。分别做ARCH-LM检验,由于二元GARCH还涉及到CU与M3、CU与M6的协方差,先对CU与M3、CU与M6的几何收益率作回归分析,然后对所得的残差序列进行ARCH-LM检验,结果如表1所示。

表1 ARCH-LM检验结果
从表1可以看出,M3的检验概率大于0.05的显著性水平,其余检验的概率均小于0.05的显著性水平。因此除M3以外,均拒绝“不存在异方差效应”的原假设,表明M6、CU的几何收益率具有异方差性,而CU与M3、CU与M6几何收益率之间的协方差亦是时变的。因此可用二元GARCH模型对上述变量的方差及协方差进行估计。
2.2 最优套期保值比率计算结果
将全部样本集分为训练样本和检验样本两部分,将原样本数据前400个作为训练样本用于计算最优套期保值比率,后200个数据作为检验样本用于比较套期保值效率。
2.2.1 静态最优套期保值比率
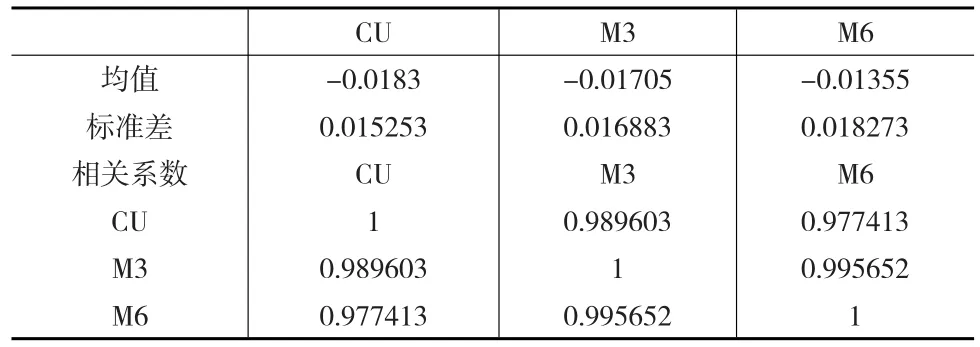
表2 训练样本数据的描述性统计
根据文献[1]研究公式,就可得到利用期限为3个月和6个月的人民币无本金交割远期结售汇合约进行套期保值的最小方差套期保值比率:hm3=0.8940,hm6=0.9031。
已知正态分布下置信度95%对应的分位数为-1.64485。那么将表2相应结果代入式(8),就可得到置信度为95%对应的利用期限为3个月和6个月的人民币无本金交割远期结售汇合约进行套期保值的最小VaR套期保值比率:hVaR_m3=0.7929,hVaR_m6=0.8045。
可以发现最小VaR方法计算的套期保值比率小于最小方差方法计算的套期保值比率。按得到的套期保值比率进行交易后锁定的检验样本集的人民币/美元汇率相对于实际汇率有明显的下降趋势,套期保值后的汇率波动基本都处于一个稳定区间,也就是说基于不同方法和残差分布下的静态套期保值均能够有效地锁定检验样本期间的人民币/美元汇率。静态套期保值效率计算结果如表3所示。
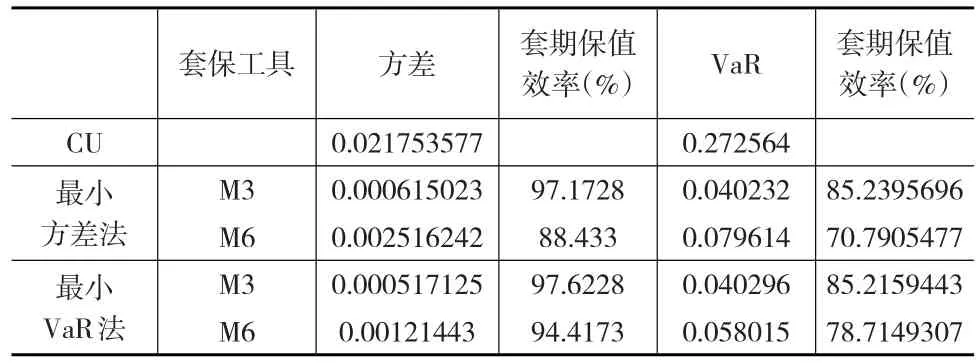
表3 不同套期保值比率计算方法及套期保值工具对应的静态套期保值效率
从表3可以发现,采用套期保值操作确实能够大幅降低外汇风险;利用最小VaR方法计算的期限为3个月的人民币NDF的最优套期保值比率的套期保值效率与利用最小方差法的效率没有明显差距,但利用最小VaR方法计算的期限为6个月的人民币NDF的最优套期保值比率的套期保值效率则要明显高于利用最小方差法的效率,这说明最小VaR方法有更强的普适性;又考虑到最小VaR方法计算的最优套期保值比率均小于最小方差法计算的,这就意味着前者需要更少的套期保值成本,因此在计算静态的套期保值比率时,最小VaR方法要优于最小方差法。
2.2.2 动态最优套期保值比率
表4和表5是利用对角BEKK方法基于训练样本计算所得的残差分布分别服从二元正态分布、二元t分布下利用3月期人民币NDF(CU与M3)、6月期人民币NDF(CU与M6)套期保值的二元GARCH模型以及方差和协方差的值。
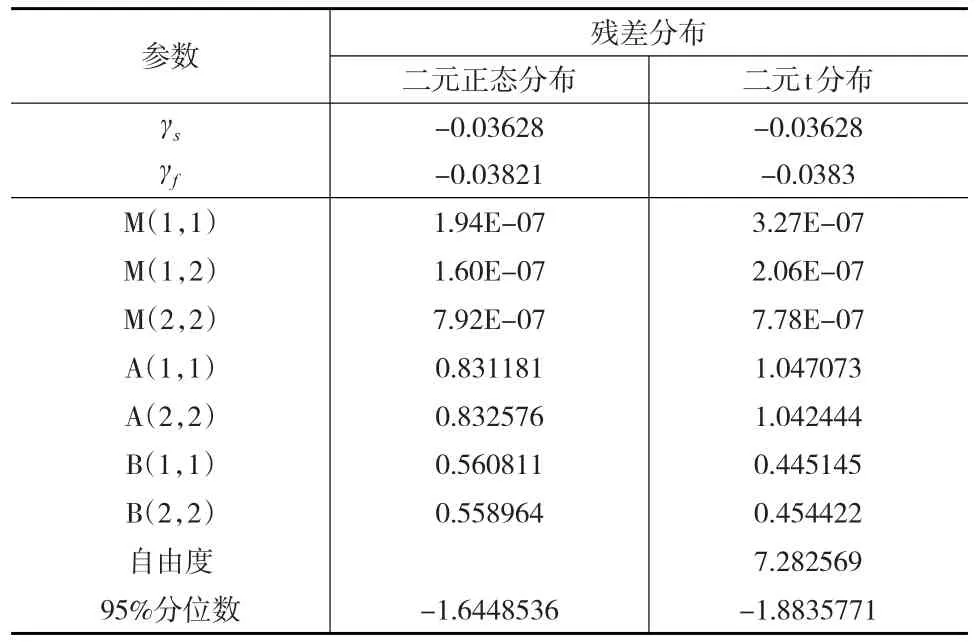
表4 CU与M3的GARCH模型参数

表5 CU与M6的GARCH模型参数
在得到CU与M3、CU与M6的时变方差及协方差后,就可以利用公式:
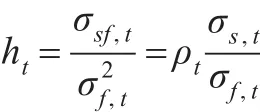
分别计算利用3月期人民币NDF和6月期人民币NDF在不同分布下的动态最小方差最优套期保值比率h3和h6,结果如图1和图2所示。
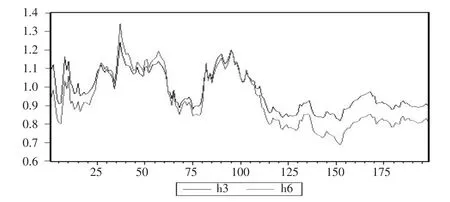
图1 二元正态分布下最小方差的最优套期保值比率动态

图2 二元t分布下最小方差的动态最优套期保值比率
利用式(8)可计算与置信度95%对应的,利用3月期人民币NDF和6月期人民币NDF在不同分布下的动态的最小VaR最优套期保值比率h3和h6,结果如图3和图4所示。

图3 二元正态分布下最小VaR的最优动态套期保值比率
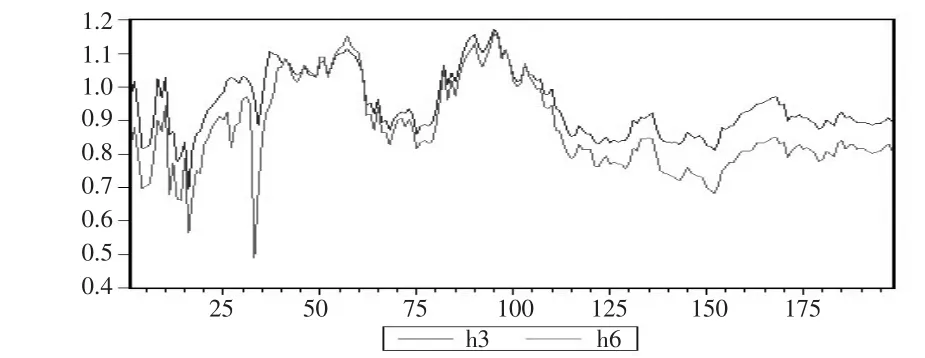
图4 二元t分布下最小VaR的动态最优套期保值比率
按得到的动态套期保值比率进行交易后,对锁定的检验样本集的人民币/美元汇率变动相对于实际汇率具有显著的下降趋势,套期保值后的汇率波动基本都处于稳定的数据区间。也就是说基于不同方法和残差分布下的动态套期保值均能够有效地锁定检验样本期间的人民币/美元汇率。
3 不同套期保值工具的效率对比
按照所得的动态最优套期保值比率对检验样本进行套期保值操作,并比较套期保值前后汇率的波动率可以计算套期保值效率。如表6所示。
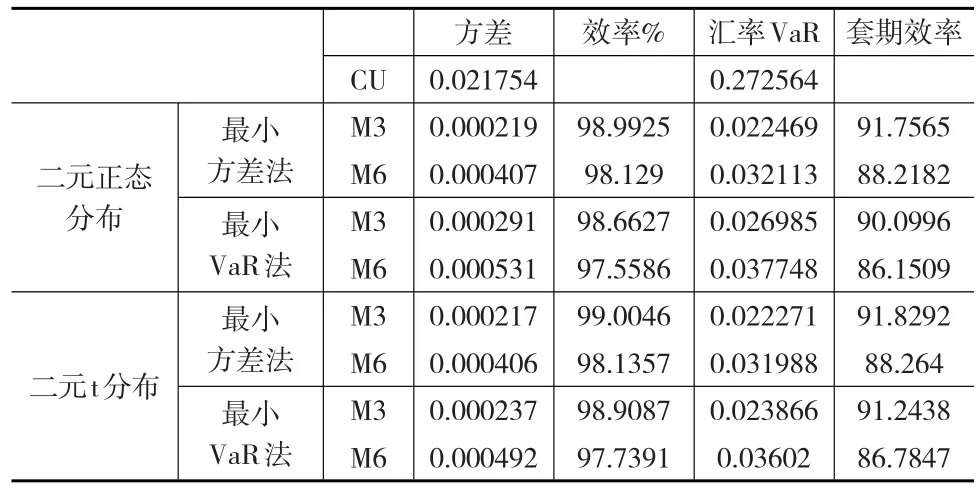
表6 不同套期保值工具对应的动态套期保值效率
从表6可以发现,残差服从二元t分布的动态最优套期保值效率略高于相应的残差服从二元正态分布的最优套期保值效率;对于不同的残差分布和套期保值工具,基于最小VaR法的动态套期保值效率均略低于基于最小方差方法的套期保值效率,但考虑到前者套期保值的成本要低于后者,因此在制定具体策略时要综合考虑;同静态套期保值的结果相似,利用6月期人民币NDF的套期保值效果普遍没有利用3月期人民币NDF套期保值的效果好;进行套期保值操作所需的成本亦将少于最小方差法的。
对比表3和表6可以发现,动态套期保值方法的效率要显著高于静态套期保值,在不考虑调整套期保值工具所需费用的情况下,企业应该选择动态的套期保值方法来制定相应的套期保值策略。在现实操作中,企业则应综合考虑套期保值的效率以及调整套期保值工具头寸所需的成本,选择最优的风险管理策略。
4 结论
本文利用最小VaR方法对人民币/美元的现汇和人民币NDF进行最优套期保值比率的实证分析,同时将GARCH(1,1)模型引入套期保值比率的计算,以期得到最优的动态套期保值比率。在利用不同的方法得到相应的最优套期保值比率后,又对他们的套期保值效果进行了比较,得出的结果如下:
(1)对于静态的套期保值而言,最小VaR方法计算的最优套期保值比率的套期保值效率要比最小方差法计算的套期保值比率的效率高。而两种方法的最优套期保值比率的计算公式又决定了最小VaR最优套期保值比率一定小于最小方差最优套期保值比率,这就意味着前者需要更少的套期保值衍生品的交易成本;而且基于最小VaR方法利用不同期限的衍生品的套期保值效率的差异也比基于最小方差法的小,说明最小VaR方法有更强的普适性。因此在计算静态的套期保值比率时,企业应优先选择最小VaR方法来制定套期保值策略。
(2)对于动态的套期保值而言,服从二元t分布的动态最优套期保值效率略高于残差服从二元正态分布的动态最优套期保值效率;对于相同的残差分布,最小VaR法的动态套期保值比率的均值和方差都小于基于最小方差的计算结果。所以在实际操作中前者需要的衍生品头寸、交易频率和幅度都要少于后者,但是前者的套期保值效率要略低于后者。因此企业在选择具体的套期保值比率计算方法时要综合考虑套期保值的效率和成本。
(3)单从套期保值效率来看,动态的套期保值明显要优于静态的套期保值,但动态的套期保值要求企业在外汇风险头寸的存续期间适时地在衍生品市场进行交易,使衍生品头寸达到最优套期保值比率的要求。因此动态的套期保值的成本就要比静态的套期保值成本高,所以企业在静态和动态套期保值之间作选择时亦要综合考虑套期保值的效率以及成本。
