考虑移动假日效应的中国月度数据的季节调整
2018-09-21王立荣周金南
王立荣,周金南
(东北师范大学a.经济学院;b.应用统计教育部重点实验室,长春 130117)
0 引言
大多数月度和季度的宏观经济数据均受到季节因素的影响。以消费品零售额为例,在公共假期之前该指标往往会出现一个峰值,因此社会消费品零售总额存在明显的季节性趋势。对月度数据和季度数据进行季节性调整的目的在于剔除季节性因素导致的数据波动。除了常规的季节性因素如趋势-周期因素、季节成分以外,中国的传统节日所产生的日历效应也对原始数据产生重要影响,尤其是中国的春节。农历春节在公历上的时间发生于每年的1月21日至2月20日之间,这会造成月度同比增长率数据仍然存在一定的扭曲,如果相邻两年的春节并非同时发生在1月或2月,就会导致同比数据的波动性可能非常大,尤其对于发电量、社会消费品零售总额、居民消费价格指数等明显受到春节因素影响的变量。
广泛使用的用于季节调整的方法是美国普查局提出的X-12-ARIMA[1]和西班牙银行提出的SEATS[2,3]。然而,尽管X-12-ARIMA程序中的regARIMA预调整模块能够实现对原始数据的预处理,即剔除日历效应(如交易日效应、移动假日效应等),但X-12-ARIMA的内置程序主要针对西方国家的情况而设计,如复活节、感恩节,对于中国的春节、端午节、中秋节等并未提供直接计算程序[4]。另外,已有的考虑中国移动假日效应的季节调整研究中,对于节前、节中、节后影响期的选取采用主观设定的方式,且对不同时间序列采用同样的影响期,因此缺乏对不同时序数据可能存在不同移动假日效应的相关研究。鉴于此,本文以中国的CPI数据为例,根据AICC准则对春节节前、节中、节后影响期进行选取,在使用X-13-ARIMA-SEATS程序包的基础上,利用R程序得到剔除春节效应的季节调整后数据,并利用调整后数据对CPI进行预测,结果表明,我国近期不会发生大的通货膨胀。
1 文献回顾
对时间序列进行季节调整的思想可以追溯到一百年前,1919年Persons明确提出将时间序列分解成趋势、周期、季节和不规则成分四个部分。对时间序列数据进行季节调整可以剔除原始数据(月度或季度数据)中的自然因素或社会历史因素,从而使数据具有可比性,并能够在宏观经济预测中正确反应基本趋势和经济周期的转折点。1954年,美国普查局Shiskin首先开发了运用计算机进行季节调整的程序,称为X-1;1955年改进的季节调整程序公布,称为X-2;到1965年已经发展为X-11方法。X-11方法是当时国际上通用的季节调整方法,也是X-11-ARIMA和X-12-ARIMA的核心[5]。
目前,X-12-ARIMA模型是最为流行的用于季节调整的模型之一。该方法最大的特征在于通过预调整模块regARIMA能够增强时间序列的ARIMA建模能力和模型选择能力,并能够估计用户自定义的回归效应,如移动假日效应、交易日效应等。具体而言,X-12-ARIMA模型首先通过regARIMA模型对数据进行预调整,如剔除移动假日效应、交易日效应等,同时选择时间序列的ARIMA模型;继而使用残差序列进行异常值检验,确定异常值类型后,通过引入哑变量的方式消除异常值的影响并重新估计ARIMA模型,循环此过程直到序列残差找不到异常值。在此过程中,实现对时间序列向前和向后的扩展。在完成一系列的预调整后,进行时间序列的季节调整,即分离出趋势性、季节性和不规则因素。
尽管X-12-ARIMA模型存在诸多优点,仍有学者对其提出质疑,即认为X-12-ARIMA模型是基于经验方法,缺乏严格的统计理论基础。因此,西班牙银行的G ó mez和Maravall提出了基于统计模型的TRAMO/SEATS程序。其中,TRAMO程序对时间序列数据进行预调整,处理移动假日效应、异常值等,然后运用SEATS程序构建ARIMA模型并对序列进行分解。X-12-ARIMA模型在构建ARIMA模型阶段对预调整数据采用了事先定义的滤波,而SEATS程序则使用ARIMA模型进行直接的信号提取,将数据分解为趋势性、季节性和不规则因素。这种分解方式假设所有成分是正交的,且趋势和季节成分捕捉到了时间序列的永久性特征。
目前,季节调整领域最新的研究成果之一是将X-12-ARIMA模型的最新版本与TRAMO/SEATS模型的最新版本合并为一个程序包,即X-13-ARIMA-SEATS程序包。X-13-ARIMA-SEATS基于TRAMO程序对模型进行自动选择,该方法综合了基于经验和模型两种方法的优点。由于该程序同时提供Genhol程序以供生成移动假日回归因子,因此有效解决了季节调整中的移动假日问题。然而,Genhol程序主要针对西方国家的移动假日,如复活节、感恩节等,对于中国的移动假日如端午节、中秋节等未提供直接的计算程序。尽管可以在R程序的seasonal程序包中调出中国历年春节发生的日期文件,但对于春节节前、节中、节后对时间序列的影响期只能选取固定期限,这也是已有研究大多固定春节影响期的主要原因。针对中国春节效应的季节调整,国内代表性的研究包括:在对中国CPI数据做季节调整的分析中,贺凤羊和刘建平(2011)[6]对春节效应的处理方式为给定三种方案。方案一,节前、节中、节后影响期均为7天;方案二,节前、节中、节后影响期分别为14天、7天、14天;方案三,节前、节中、节后影响期分别为20天、7天、20天。依据综合指标Q值分别选取了方案二和方案三。栾惠德和张晓峒(2007)[7]在对中国社会消费品零售总额进行分析时,将春节效应的影响设定为节前影响期为20天,节日期间影响期为7天,节后影响期为20天,尽管文中也提及了需要根据一些指标来选择各子区间长度,但未给出明确的指标选取标准。类似的,王群勇和武娜(2010)[8]在对中国社会消费品零售额月度数据进行季节调整的研究中,考虑了诸多移动假日(春节、中秋节、清明节、端午节等)效应、黄金周效应等,但对春节效应的分析中将节前、节中、节后的影响天数分别设定为20天、5天和10天,仍然具有一定的主观性。由于不同时间序列受到移动假日效应的影响可能是不同的,因此,有必要运用合理的指标对移动假日效应的影响期进行相对客观的判断。鉴于此,本文结合Roberts和White(2015)[9]的最新研究成果,利用AICC准则对春节效应影响期进行客观选取。具体地,运用X-13-ARIMA-SEATS程序包,通过R软件调用该程序包和Genhol程序,以中国CPI数据为例,对中国的时间序列数据进行季节性调整。
2 模型介绍
2.1 计算CPI定基比数据
在对时间序列数据进行季节调整之前,应该首先确定是否需要对原始数据进行必要的处理。以CPI数据为例,国家统计局公布的CPI数据为同比数据和环比数据,同比数据一定程度上可以消除季节性因素,但由于移动假日效应和“翘尾因素”的影响,其并非是消除季节因素的最佳方法。另外,在对中国的CPI同比增长率数据进行观察可以发现(见图1),其呈现出的季节性效应并不是十分明显。考虑到CPI同比增长率数据受到“翘尾因素”影响,发达国家通常对月度定基CPI进行季节调整[10]。

图1 2001年1月至2017年2月CPI同比增长率
将同比数据转换成定基比数据通常有两种做法,第一种将某年选定为基准年后,假定当年各月CPI初始值均为100,然后利用同比数据计算样本期内的定基比数据。第二种可以假定基准年1月份的初始值为100,利用基准年的环比数据计算出基准年各月度定基比数据,再利用同比数据将样本期内的CPI数据做定基处理。本文选取2001年作为基准年,分别采用两种方法将同比数据转换为定基比数据,结果见图2。图2中标记为CPI的曲线为利用第二种方法计算的CPI定基比数据,位置相对靠上的CPI’曲线代表利用第一种方法计算的CPI定基比数据。定基比数据相较同比数据呈现出更强的季节性特征。

图2 2001年1月至2017年2月CPI定基比
2.2 对CPI定基比数据进行季节调整
在对CPI数据做常规的季节调整之前,需要剔除移动假日效应,即春节的影响。剔除春节效应主要通过引入虚拟变量的方式,该思想来自Bell和 Hillmer(1983)[11]。
需要构建的虚拟变量如下:

i=1,2,3分别代表节前、节中、节后,τit为时间t中i部分影响的天数,τi为i部分受到春节影响的总天数。举例来说,如果 τ1=τ2=τ3=5 ,即春节节前、节中、节后对时间序列数据产生影响的天数均为5天,并假设某年春节前一天为1月31日,则节前影响落入1月份的天数为5天,节中影响落入1月份1天、落入2月份4天,节后影响落入2月份5天,因此:

即为剔除该年春节影响因素而构造的三个虚拟变量向量(如式(2)所示)。
以往对于春节节前、节中、节后影响天数的研究通常以常值处理(如本例中选取τ1=τ2=τ3=5,前文中提及的王群勇和武娜(2010)[8]、贺凤羊和刘建平(2011)[6]的研究均主观选取固定影响期)。对所有时间序列变量不加区分,选择同样的子区间影响长度显然是不合时宜的,没有考虑不同变量可能存在的不同特征,因此,本文参照Roberts和 White(2015)[9]的方法,依据法定春节放假时间为7天,故节中影响期τ2选为7天,而节前、节后影响天数为0~20天,循环调用相关程序并根据AICC最小准则进行选取。具体的,适用于有限样本容量的AICC准则可以表示如下[12]:
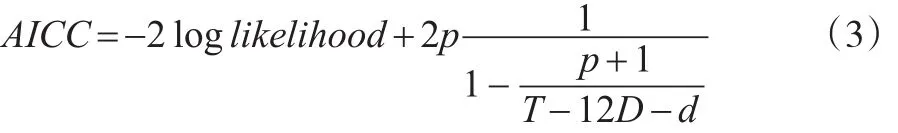
其中,p为估计参数的个数,D是季节差分的阶数,d为常规差分的阶数,T为样本容量,loglikelihood是估计参数的对数似然函数值。
依据AICC最小原则,在剔除了春节效应以后,可以进行常规的季节性调整。由于端午节、中秋节的法定假日天数仅为1天,其对月度数据产生季节性影响的可能性较小,因此,本文仅考虑春节的移动假日效应(根据Ivan Roberts和 Graham White(2015)的结论,端午节、中秋节对CPI的影响不显著)。
3 实证结果
本文对CPI定基比数据进行季节调整的样本区间选用2001M1-2016M3,而2016M4-2017M3的数据留作与模型预测值进行对比。
根据AICC准则,模型最终选取节前影响期为15天,节后影响期为8天。表1为采用AICC准则对经对数转换的CPI定基比数据进行季节调整的主要统计量。
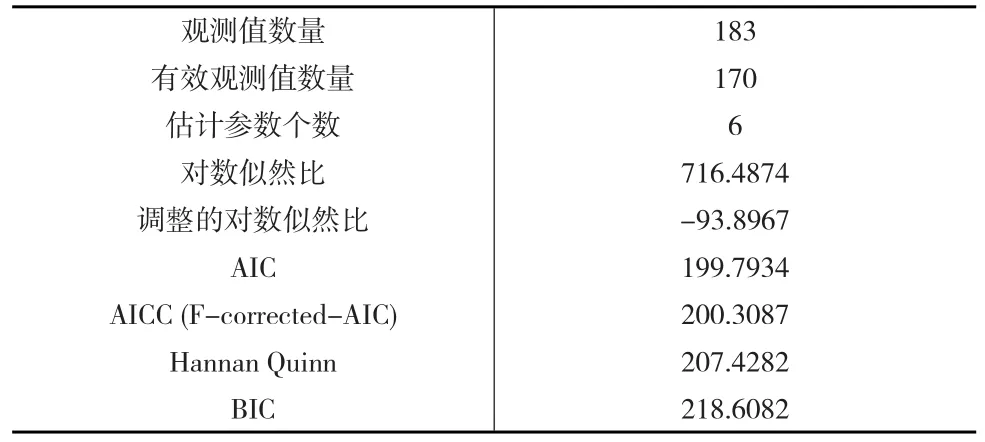
表1 经对数转换的CPI季节调整模型主要统计量
程序最终选择的ARIMA模型为(3 1 1)(0 1 1),且春节因素对应的三个虚拟变量均显著(如表2所示),表明CPI定基比数据的确受到春节因素的显著影响。另外,模型识别出2008年2月为LS异常值,即水平移位异常值(level shift outlier)。

表2 回归模型
将经过季节调整后的数据与原始的CPI定基比数据绘制在图3中可以发现,经过季节调整的数据很好地剔除了季节性因素的影响。
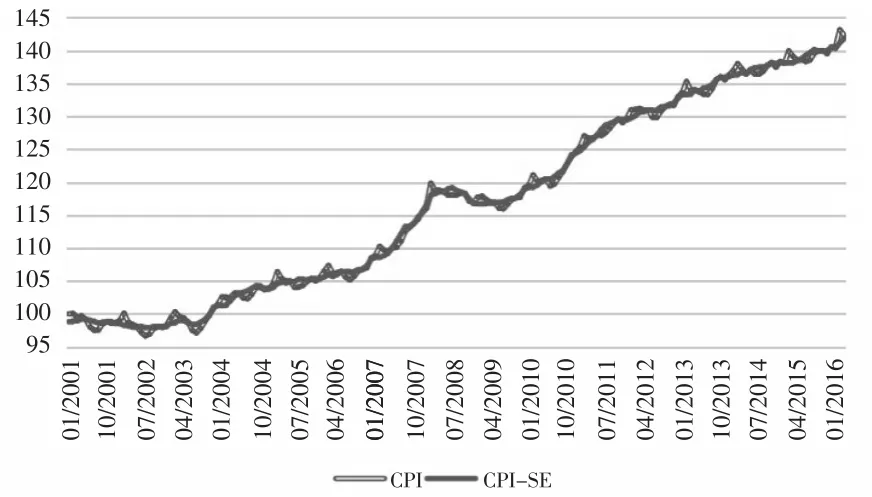
图3 2001年1月至2016年3月CPI与季节调整后的CPI数据图
4 CPI的预测
根据选择的模型对CPI定基比数据进行预测,预测的时间区间是2016年4月至2017年3月(见图4)。从预测误差可以看出,半年内的预测误差基本在1%左右,仅最后3个月的预测误差超过了1%,但仍控制在2%以内,预测精度很高。
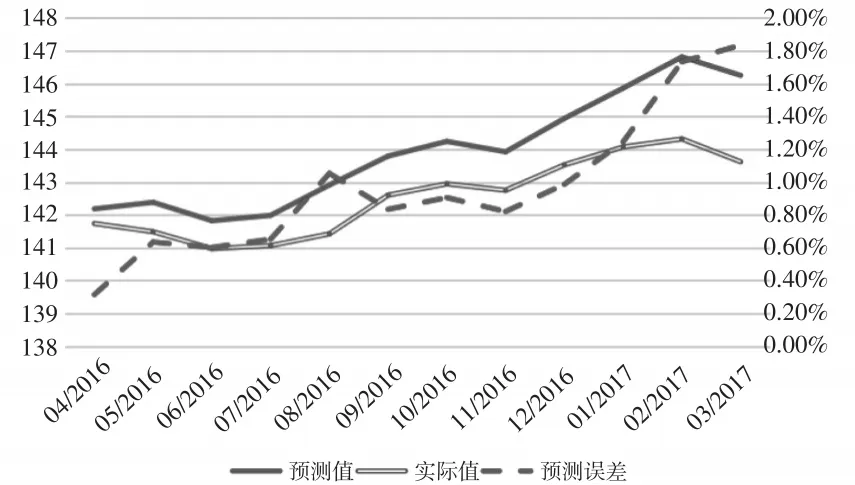
图4 2016年4月至2017年3月CPI定基比数据预测结果
在此基础上,结合2017年4月至12月模型对CPI定基比的预测数据,通过换算得到同比CPI数据,具体结果见下页表3。从表3的CPI同比预测数据来看,至2017年年底,中国的物价水平将总体保持稳定,不会出现大的通货膨胀。

表3 2017年4月至12月同比CPI预测值
5 结论
为了更好地监测国民经济运行状况,需要对经济数据尤其是月度、季度等高频数据进行科学地处理,发达国家普遍采用季节调整后的数据作为经济分析和预警的基础。我国在对经济数据进行季节调整方面已经针对中国国情研发了中国人民银行版X-12-ARIMA软件和国家统计局版NBS-SA软件,由于两款软件均未实现对外开放,因此季节调整之前对中国移动假日效应进行预处理方面,尤其是春节效应的影响期,是否对不同经济指标运用合理的标准加以区分不得而知。已有的对中国经济数据季节调整的研究在处理移动假日效应时均采取固定影响期,对不同经济指标不加区分,这就忽略掉了指标间可能存在不同特征的事实,在预测方面将不可避免地存在偏差。本文结合Roberts和 White(2015)[9]的最新研究成果,利用AICC准则对春节效应影响期进行客观选取,以中国的CPI定基比数据为例,展开了相关分析,并进行了样本内和样本外预测。样本内预测的误差均低于2%,且半年内的短期预测误差基本低于1%,表明模型的预测精度很高。样本外预测的结果则表明,中国的物价在短期内不会出现大幅度的上涨,将处在相对稳定的区间。另外,本文对数据的季节调整处理方式可以推广至其他移动假日效应。
