水资源消耗预测的异常值检测及缺失数据填补方法
2018-09-21宋晓娜薛惠锋王海宁
张 峰,宋晓娜,薛惠锋,王海宁
(1.山东理工大学 管理学院,山东 淄博 255012;2.中国航天系统科学与工程研究院,北京 100048;3.泰山学院 商学院,山东 泰安 271000)
0 引言
水资源消耗预测是根据水资源消耗量、社会、经济等相关历史时序数据,挖掘水资源消耗动态演化规律及其影响要素之间的作用机理,并构建水资源消耗预测模型,辨识水资源消耗程度未来变动趋势。因此如何实现高精度的水资源消耗预测对于保障水资源综合规划、水资源管理等政策制定的科学性与合理性至关重要。而要达到上述目标,需以完整、高质量的历史时序数据为基础,但是限于现有监测指标与统计手段等因素的约束,其历史数据收集中难免存在数据异常、缺失等状况。其中,数据的异常可主要分为实际突变异常和待修正异常2类,前者是指标数据由于实际消耗等而产生的实际改变,检测与统计过程中需对其进行保留,而后者主要是在人为操作、设备使用、统计口径差异等因素影响而导致数据出现“存在而不正常”现象;缺失数据则是监测设备的损坏、数据资料的遗失等造成的“数据空白”[1]。对于待修正异常与缺失数据均需要采取有效的检测与填补方法进行完善,以支撑水资源消耗预测建模的要求。考虑由于水资源的自然与社会经济双重属性而导致影响水资源消耗的因素具有复杂多样性与不确定性,本文在现有研究成果的基础上,应用偏最小二乘(Partial least squares,PLS)与最小残差回归法、粒子群(Particle swarm optimization,PSO)与最小二乘支持向量机(Least squares support vector machine,LSSVM)分别对水资源消耗预测的异常值进行适用性研究,为提升水资源数据管理水平提供一定的方法支持。
1 模型构建
现有诸多研究成果中对水资源消耗与社会经济发展之间的强相关性进行了论证[2,3],同时鉴于社会经济指标可通过其统计年鉴取得较高可信度的数据,对此考虑选取偏最小二乘法对年均水资源消耗量与社会经济发展指标之间的主成分进行提取处理。毛李帆等[4]认为该过程中基于相关指标数据构建的回归模型会受异常值的扩大影响,对主成分的贡献水平显著高于常规数据,并在电力负荷异常数据分析中得到验证。因此本文利用统计数据样本对提取的主成分贡献程度的方法检测水资源数据异常值。
1.1 基于PLS-Q2的异常值检测模型
设因变量Y和 p个自变量构成自变量集合 X=(x1,x2,...,xp),观测n个样本点,并构成n维因变量向量(y1,y2,...,yn)n×1和自变量构成n×p观测矩阵X=(x1,x2,...,xp)n×p。PLS 回归的基本原理是逐次对自变量 X提取主成分qα,α=1,2,...,α ,尽可能多地概括自变量集合 X 中的信息,同时与因变量Y的相关性可以达到最大值。对此,定义Q为数据样本i对第v主成分qv的贡献度,即:



可推出,若:

则可判定数据样本i对主成分qv的贡献度偏大。多数情况下对于样本信息可通过2个以内的主成分进行概括提取,对此本文假设主成分数目为2,即α=2,则将判定条件转为:

1.2 基于最小残差的异常值修正
考虑传统最小二乘回归对于其方差的非稳健性,易导致其拟合效果偏向突变数据扩散,本文拟采用最小残差的回归方式修正最小二乘回归目标函数,削弱突变数据对拟合模型的影响。其函数为:

其中,Wi指水资源数据样本值;Hi指影响要素指标;ϑ是待估系数;υi指数据样本拟合误差。对于上述公式,可假设:
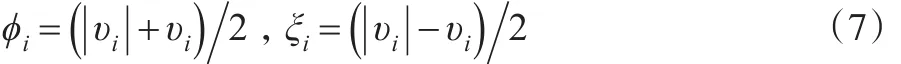
即:

将式(8)代入到模型(6)中,求解规划解:

根据上述模型,可知利用一次函数作为基于最小残差异常值修正的目标函数,可有效控制其模型对水资源异常值的敏感度达到修正效果。
1.3 基于LSSVM的缺失数据填补
考虑数据样本的规模及LSSVM在解决非线性、小样本等方面问题的拟合优势[5],本文选取该方法对水资源缺失数据进行补充。同时,利用粒子群算法优化LSSVM核函数的参数。步骤如下:

其中,ρ(x)指非线性变换映射函数;ω指权系数;b是偏置量。据此,LSSVM目标函数可写为:

其中,θ是误差变量;γ为惩罚因子(γ>0)。引入Lagrange函数求解:

式中ϖi指Lagrange乘子。按照Karush-Kuhn-Tucker条 件[6],分 别 测 算 ∂L ∂ω =0 、∂L ∂b=0 、∂L ∂θ =0 和∂L∂ϖi=0,取得方程组:


鉴于RBF核函数处理非线性输入与输入关系的适用性,本文采用其作为LSSVM的核函数:

1.4 基于PSO的LSSVM参数优化
通常对LSSVM模型参数γ与ϖ的优化多采取参数空间穷尽搜索算法,但该方式难以参数的阈值范畴进行合理界定,对此,本文利用PSO优化其参数,同时为避免PSO收敛陷入局部极值,在初始粒子群选取时利用平均粒距函数对其离散程度进行测定[7]:
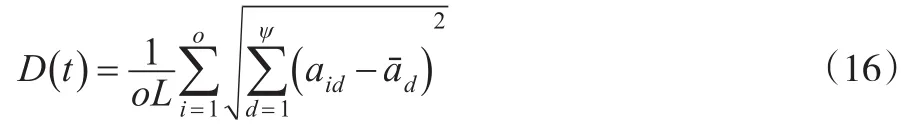
其中,ο为种群粒子数;L为搜索区域对角最大距离;aid表示粒子i的d维坐标,而指其平均值。
此外,对于PSO粒子是否出现早熟收敛的判定,可依据种群粒子适应值的改变来分析种群状态,即设定粒子适应度为Ri,种群平均适应度,定义其适应度方差:


选取参数优化后的LSSVM模型,将除了存在数据缺失以外的社会经济指标作为模型输入,而水资源消耗值作为模型输出进行样本训练拟合,进而根据拟合结果对水资源消耗缺失值进行补充。
2 算例分析
2.1 水资源数据异常值检测算例与分析
以广东省2000—2015年社会经济发展与水资源消耗量为例①社会经济指标主要源于《广东省统计年鉴》(2000—2016),水资源消耗量通过求解地区用水总量与再循环水资源量之差而得,由于再循环水资源量测算过程较为复杂,需要对计算结果进行二次检查,其数据源于《广东省水资源统计公报》(2004—2015)、《广东省环境统计公报》(2000—2015)。,其指标数据见表1。利用PLS-Q2模型对其2000—2012年历史数据进行函数拟合,同时检测水资源异常数据,根据拟合结果完成异常值修正并预测2003—2015年数据,检验模型预测有效度。
按照表1中数据,利用PLS模型对其指标数据进行主成分提取处理,并利用模型(2)测算各数据样本的累计贡献度Q,见表2。其中,r1、r2分别表示主成分1与主成分2。
根据表2可知,2007年、2011年和2012年的数据样本累计贡献度Q均已突破0.25水平,并分别达到0.390802、0.259432和0.268102,与其他样本之间数值差异相对显著。对此,参考时序历史数据,选取模型(3)显著水平τ=0.15。按照模型(7)测度Q2椭圆式:
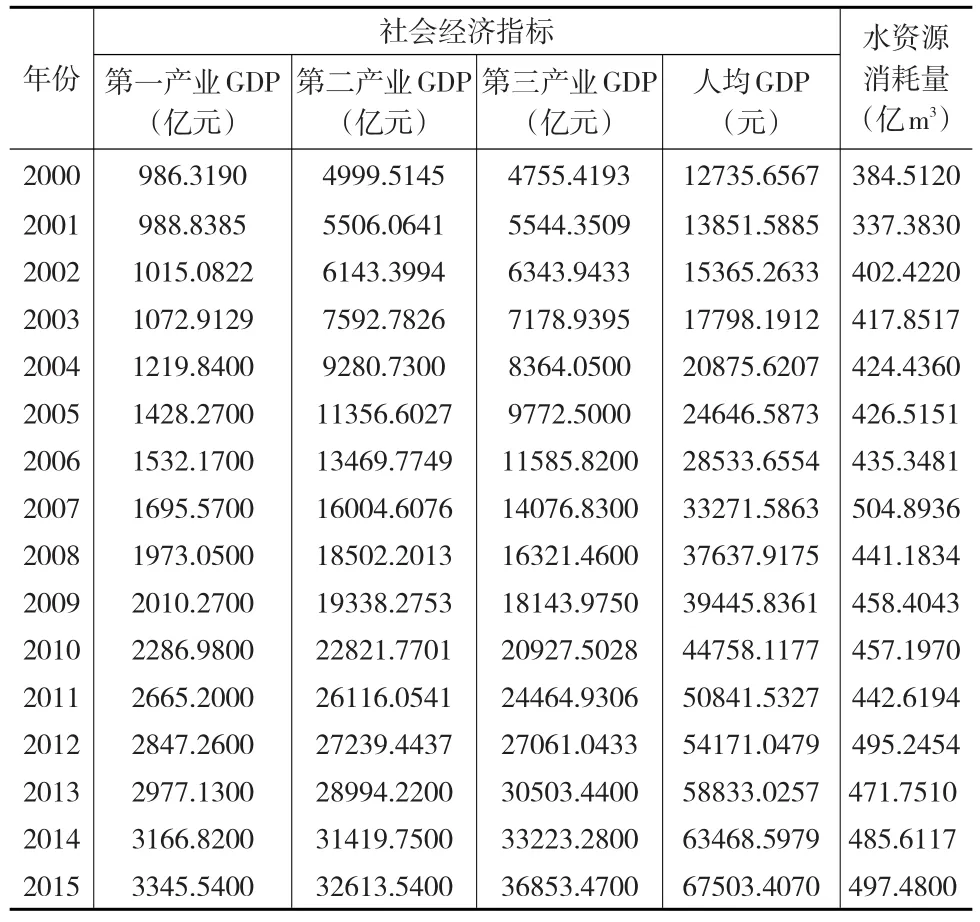
表1 广东省社会经济与水资源消耗指标

表2 主成分r1与r2测度结果

按照式(19)及表2,可绘制其Q2椭圆分布图,见图2。

图2 异常值修正前Q2椭圆图
图2所示的2007年、2011和2012年数据样本点靠近Q2椭圆的边缘,需对其进行核定。经对于统计数据重新测算核定,发现2007年和2012年水资源消耗量数据应分别为450.8936和459.2454,而2011年数据(442.6194)与核定数据相一致,即为实际突变数据。如果按照水资源消耗均值数据±5%水平作为划分依据,则处于(411.278,454.570)以外数据均被列为异常值,即2000—2002年、2007年、2009—2010年和2012年为异常点;而若以±10%水平为标准,(389.6315,476.2163)为其正常区间,除了2007年、2011年和2012年以外,2000—2001年也被误列为异常值点。可见,利用传统均值±5%与±10%水平的评判方法虽然在操作上具有简便性,但易造成较大的误判,而PLS-Q2模型表现出了较强的实用性。
对于重新核定的数据,建立Q2椭圆式,见模型(20),而其主成分与Q2椭圆分布见图3。


图3 异常值修正后Q2椭圆图
观测异常修正前后Q2椭圆图,可知2007年、2012年数据样本点向圆心靠拢,表明由于人为操作等主观因素造成的异常值已被修正。而2011年数据为水资源消耗实际突变数据,仍置于椭圆边界处,对其无需进行调整。
考虑异常值对拟合方程的影响,利用传统最小二乘法与本文构建的最小残差的异常值修正模型分别对数据修正前与修正后样本进行回归分析,依次记为ℓ1(x )、ℓ2(x),再预测2013—2015年水资源消耗量。各拟合模型如下:
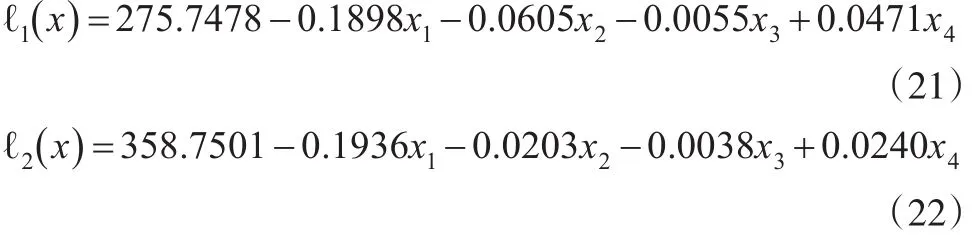
其中,x1,x2,…,x4分别指表 1中各产业 GDP 与人均GDP量。据其取得水资源消耗量预测值,见表3。

表3 ℓ1()x、ℓ2()x回归预测结果
据表3,可知传统最小二乘法测度的ℓ1(x)相对误差均大于0.15水平,而基于最小残差的异常值修正模型ℓ2(x)的预测相对误差最高值为0.063434,其余均低于0.04水平(0.038418、0.039577)。这说明通过对水资源消耗量异常值进行修正,构建基于最小残差的异常值修正模型在对其进行预测分析中具有相对较高的精度,可满足对水资源消耗数据时序动态规律挖掘的需求。
2.2 水资源数据缺失填补算例与分析
以广州市2004—2015年水资源消耗与社会经济相关指标数据为例,并假设其2008年与2013年水资源消耗量为缺失值,见表4。

表4 广州市社会经济与水资源消耗指标
根据表4,将社会经济指标作为PSO-LSSVM输入,而水资源消耗量作为输出。其中,进行PSO测算时,惩罚因子γ∈[0 . 1,100] ,∈[0 . 1,10],对此参考样本数据设置 γ=30,=2,粒子数ο=30,最大迭代次数tmax=100;平均粒距可反映种群分布的多样特征,随机粒子产生的粒距D(t)均不低于ϖ,设其阈值ϖ=0.001;适应度方差表征粒子聚集水平,设其阈值ε=0.01。而表4中各指标归一化模型如下:
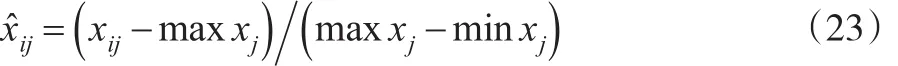
其中,xij指社会经济与水资源消耗原始数据;ij指归一化后指标值;xj表示xij所在 j列数值。利用RBF核函数,结合模型(15)对除2008年、2013年外的其他数据分别进行LSSVM、PSO-LSSVM模型样本训练。基于训练拟合模型对其缺失数据点进行填补,结果见表5与下页图4。

表5 模型拟合结果

图4 水资源消耗量模拟曲线
据表5和图4可知,通过LSSVM模型可对水资源消耗量达到一定水平的拟合效果,样本测度期内最大相对误差为0.027541,平均相对误差0.0036,而基于PSO-LSSVM的水资源消耗量拟合模型通过引入逐步寻优参数与更新粒子位置,避免了对γ、选择的盲目性和随机性而陷入局部极值的弊端。通过图5对比LSSVM和PSO-LSSVM的相对误差,除于2004年以外,PSO-LSSVM模型在其余样本年份数据的测度中均呈现较高精度拟合,平均相对误差为-0.0006。通过上述两种方法分别对2008年、2013年水资源消耗量缺失数据进行填补,LSSVM拟合值为680047万m3、613497万m3,PSO-LSSVM拟合值分别为683713万m3、604572万m3,而实际水资源消耗统计值为689216万m3和602272万m3,相对误差对比中LSSVM达到0.005391、-0.014548,PSO-LSSVM则为-0.001177、0.003819,该结果进一步印证了PSO-LSSVM模型在水资源消耗拟合中可实现更精准的数据填补效果。

图5 拟合误差对比
3 结论
在基于社会经济相关指标具有较高可信度的前提下,本文运用PLS-Q2方法对水资源消耗预测中的历史时序数据所存在的异常值进行检测辨识,基于最小残差的异常值修正模型对拥有实际突变异常数据序列进行了预测验证,再通过PSO-LSSVM模型对水资源消耗数据缺失样本进行了拟合填补。结果表明:(1)利用PLS方法提取水资源消耗及社会经济指标数据主成分及其累计贡献度的Q2椭圆图,可合理辨识出水资源消耗时序数据中异常点;(2)相比传统最小二乘回归,基于最小残差的异常值修正模型可有效缓解实际突变数据对水资源消耗预测的拉伸影响,其回归预测精度更高;(3)对于水资源消耗缺失数据的填补,LSSVM与PSO-LSSVM均呈现出较高的拟合效果,但同比之下PSO-LSSVM相对误差更小,对其缺失的数据填补更加准确。
