基于神经网络与非参数核方法CPI的ARMA预测与非线性改进
2018-09-21孙冠华
孙冠华
(南京大学 经济学院,南京 210093)
0 引言
近年来,学术界对回归函数拟合的研究,无论在线性或非线性领域,新理论、新方法层出不穷,拟合精度越来越高,误差也越来越小。然而,对时间序列的预测问题在理论和实证方法上却都鲜有突破,主要是因为在一个价值观念越来越多元的社会里,新事物、新变化的快速产生使原序列发生变异的几率增加,时间序列所包含信息越来越多,因而准确预测变得越来越难。在这方面,王维和范彦伟(2012)[1]针对CPI时间序列的非线性特征,利用混沌神经网络构建预测模型,预测结果表明该模型在6个月内具有较高的精度;程建华和于戒严(2014)[2]利用向量自回归(VAR)模型对2014年CPI各个月的值做出预测,结果显示全年将现“先抑后扬”态势,涨幅约2.4%。杨新臣和吴仰儒(2010)[3]将小波分析和支持向量回归(SVR)方法引入CPI预测问题,新方法充分提取CPI时间序列各种隐周期和非线性,可以显著提高原时间序列的预测精度。本文采用的几种预测方法对CPI预测问题也有改进作用,其中用核方法进行预测所得结果的最大改进幅度为65.40%。
1 CPI的ARMA预测
1.1 平稳性检验
时间序列的平稳性是ARMA模型建模的基础,本文选择CPI序列样本期为1990年1月到2017年1月,共计325个样本。选取ADF方法检验CPI序列的平稳性,原假设为序列不平稳。经计算,原序列的Dickey-Fuller统计量为-2.8902,p值为0.2011,不能显著拒绝CPI序列不平稳的假设,因而不能直接对CPI序列进行ARMA模型建模。
对原CPI时间序列进行一阶差分,对差分之后的序列进行平稳性检验。经ADF检验,差分后序列的Dickey-Fuller统计量为-4.0376,p值为0.01,序列为平稳序列,因而可以用差分之后的CPI序列进行ARMA模型的建模。
1.2 ARMA模型对差分时间序列的建模
1.2.1 长期预测情形
记差分之后的CPI时间序列为ΔCPIt,即ΔCPIt=CPIt-CPIt-1。考虑到ARMA模型是线性时间序列分析中的经典模型,这里用其对ΔCPIt时间序列进行估计和预测。首先对模型进行定阶,对于时间序列的定阶,比较经典的法则如AIC和BIC准则。但由于ARMA模型具有形式上的特殊性,Tsay和Tiao(1984)[4]提出EACF方法确定ARMA模型的阶数。取前240个样本为训练样本,后85个样本为预测样本,计算得ΔCPIt序列的EACF定阶图如图1所示。
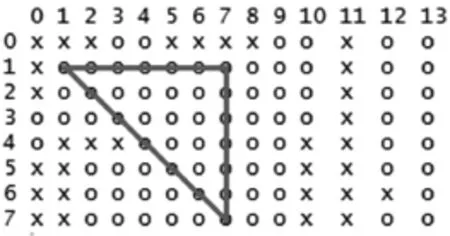
图1 差分CPI序列EACF定阶图
其中横向为MA模型的滞后阶数,纵向为AR模型的滞后阶数,交叉处圈表示用对应ARMA模型拟合结果不显著,交叉处叉号表示结果显著。阶数的最终确定采用三角形法则,即以全部由圈围成的三角形的最左上方顶点对应的坐标为ARMA模型的阶数,这里阶数确定为(1,1),模型表达式为:

其 中 (θ0,θ1,β1,σ2)′是 参 数 集 ,et是 服 从 正 态 分 布N(0,σ2)的随机变量。采用条件最小二乘法估计参数,得到参数最终估计为(-0.0037,-0.4249,0.7194,0.60)T,拟合误差范数为52.306。图2是用前240个观察值,即从1990年1月至2009年12月的真实CPI时间序列数据绘出的拟合效果示意图,其中实线为真实样本数据,虚线为拟合函数。

图2 ARMA模型CPI走势拟合效果图(1990.1-2009.12)
本文采用ARMA模型对后85个CPI月度数据(2010.1-2017.1)进行预测,预测误差范数为12.528。图3是预测效果示意图,从图中可以看出,预测偏差较大,尤其是在与预测始点相距步数较多的点上,ARMA模型的预测几乎为常值,未能有效反映实际CPI序列的变化情况,带来了较大的误差。究其原因,一是相比于短期预测,长期预测本身具有难度大、精度不高的特点。二是作为反映市场一篮子物价的重要指标,CPI的变化受到宏观经济政策影响较大,因而其时间序列表现出一定的非线性特征[5]。而ARMA模型是经典线性模型,对CPI序列的非线性部分进行描绘时偏差较大。

图3 ARMA模型真实CPI数据预测效果图(2010.1-2017.1)
1.2.2 短期预测情形
进一步地,可以用以上的方法以ARMA模型对CPI时间序列作出短期预测。这里选取1990年1月至2014年的CPI数据作为训练样本,共计300个。以2015年1月至2017年1月的CPI数据作为预测样本,共计25个。根据与上文中相同的计算方法,得到ARMA模型短期预测误差为3.599,预测效果图如图4所示。

图4 ARMA模型真实CPI数据预测效果图(2015.1-2017.1)
2 ARMA预测模型的非线性改进
针对ARMA模型未能有效刻画CPI序列中的非线性因素导致预测精度不高的结果,本文尝试神经网络、核方法等几种非线性方法,考察其能否对预测精度有所提高。
2.1 神经网络模型[6]
(1)长期预测情形
在变量之间的函数关系不明朗时,利用神经网络进行建模是优先选择的方向。在建模时,神经网络模型不要求建模者提供具体的函数,函数关系被当作模型的“黑箱”进行处理。建模者只需提供输入、输出进行训练,并用训练好的网络进行模拟。神经网络对函数预测问题的处理为建模者提供了方便,同时模型能够保持良好的精度。丁刚等(2006)[7]指出,只要有足够多的隐含层数和足够多的神经元数目,神经网络可以以任意精度逼近任意连续泛函。因此,在本文中,以时间序列{C PIt-1,t=2,...T } 为输入,以时间序列{C PIt,t=2,...T }为输出进行训练,用逐步预测法对CPI时间序列预测问题进行研究。基于各类神经网络应用普遍性不同,本文依次采用应用较广的BP网络和RBF网络模型进行训练和预测。
BP(Backpropagation)网络是将Widrow-Hoff学习算法拓展至非线性可微传递函数和多层神经网络而得到的网络模型。BP网络是多层前馈型神经网络,其核心是误差反向传播算法,在反向传播的过程中调整权值和阈值、减小误差。隐含层传递函数要求是可微函数,一般采用Sigmond函数,即y=(1+e-x)-1。BP网络可以有多个隐含层,因而要提高BP网络的预测精度可以有两种基本选择:第一种是增加隐含层的个数,第二种是增加每个隐含层上的神经元结点数目,或者也可以将两种方法一同加以运用。
表1列出了用BP网络模型对原CPI进行拟合和预测的误差分布情况,其中体现了以上两种增加预测精度方法的运用。

表1 BP网络模型CPI序列长期预测误差情况表(2010.1-2017.1)
从表1的结果来看,对于隐含层数为1的BP网络,较多的神经元结点数带来的改善程度较高;在存在多个隐含层的情况下,达到相似精度需要的每层神经元结点数较低;增加神经元层数可以增加改善预测精度的概率。总体来看,这些结论都是符合直觉的。
RBF(Radical Basis Function)网络是3层前向型神经网络,只有1个隐含层,没有误差反向传播机制。若要求结果与期望输出的误差较小,需在隐含层设置比BP网络隐含层更多的神经元数目。RBF网络使用的径向基函数一般为高斯函数,即 y=exp(-x2/(2δ2)),其中δ为固定常数。指数函数的强衰减性使得只有输入落在空间中一个很小的指定区域时,隐含层神经元才可以做出非零的响应,因而也说明了需要更多的隐含层神经元来达到指定的精度。在RBF网络的建模应用中,扩展系数(sc)是其中的关键参数,应根据神经元数目与训练样本、目标样本以及拟合误差情况进行合理选择。
表2报告了用RBF网络对原CPI时间序列进行长期预测的误差,同时报告了设定误差目标、扩展系数以及预测误差范数。

表2 RBF网络CPI序列长期预测误差情况表(2010.1-2017.1)
从表2中可以看到,RBF网络的长期预测效果不佳,对于大部分情形,RBF网络长期预测误差大于ARMA模型长期预测误差。扩展系数对RBF网络计算精度有重要影响,改变扩展系数预测误差也随之改变。
(2)短期预测情形
用以上相同的方法,以1990年1月至2014年12月的300个CPI数据作为训练样本,对剩余的2015年1月至2017年1月的25个样本进行预测,可以得到BP网络短期预测结果如表3所示。

表3 BP网络CPI序列短期预测误差情况表(2015.1-2017.1)
从表3中可以看到,相对于长期预测(表1),BP网络模型的短期预测精度比ARMA模型有较大提高,最大提高幅度为49.18%。表4报告了RBF网络短期预测的结果。
从表4中可以看到,与BP网络模型相似,RBF网络在短期预测精度方面比ARMA模型有较大的提高,最大提高幅度为51.85%。
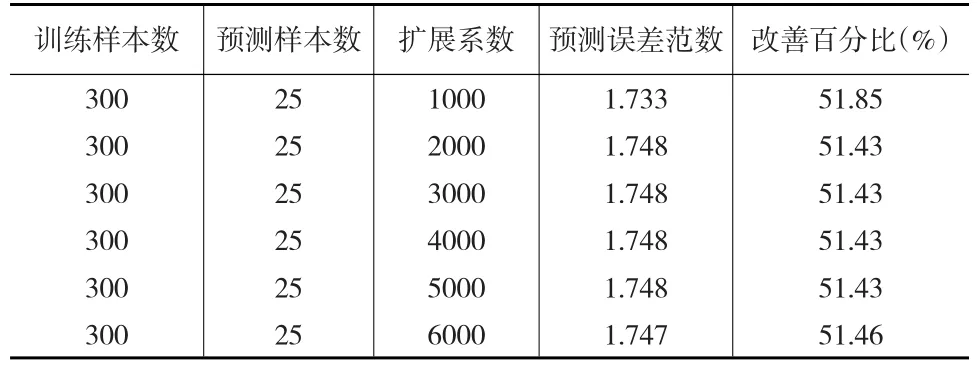
表4 RBF网络CPI序列长期预测误差情况表(2015.1-2017.1)
2.2 非参数模型
近年来,随着经济模型化趋势得到学界认同,主流经济学文献中的数理模型数量持续增加,经典参数模型的固有缺陷也逐渐显现。首先,经典参数模型需要预先设定总体的分布形式,以正态分布和t分布为常用分布。但实际上,这些常用的分布形式在经济生活中并不常见,因而用以这些分布为前设的参数模型进行估计和计算时会引入误差。其次,精准拟合参数模型需要的样本量较大,虽有些可以用大数据作为支撑,但也有捉襟见肘的时候。
非参数模型可以较好地弥补这两方面的缺陷。同时,大幅预测精度的提高是可能的。
第一,非参数模型更多应用的是样本在总体中位置,即样本秩的信息,而并不需要具体的分布形式,解决了分布错误设定引入的误差问题。
第二,非参数方法在样本量较小的情况下就可以得到令人满意的结果,大大降低了结果对样本数量的依赖性,这是对参数模型的重要改进[8]。
Nadaraya和Watson在1964年同时提出的核方法是一种常用的非参数方法,对于函数拟合和预测等问题都有良好的效果。核方法中较为重要的参数是窗宽,对窗宽的选取有交叉验证法、列举法等几种方式,最优窗宽对应的误差最小,窗宽选取太大或太小都将增大误差。
(1)长期预测情形
本文用列举法选择窗宽。根据经验,在解释变量极差0.15倍左右的窗宽为最优窗宽。因此本文构造以5为起点,0.05为步长,10为终点的窗宽序列,每次实验选择一个窗宽,并以序列{C PIt, t=2,...,240} 作为被解释变量,序列{CPIt-1, t=1,...,239} 作为解释变量。此时 ARMA 模型预测误差为12.528。用公式(2)进行一步预测:

每步预测值加入下一步的解释变量并拟合,得到第二步的预测值,这里的Kh(x)=K(x/h)/h是标准化后的核函数。如此重复25次得到预测结果及误差,选择使得误差范数最小的实验对应窗宽为预测窗宽。表5中列举了误差较小的几次实验对应窗宽。

表5 核方法长期预测窗宽及对应误差表(2010.1-2017.1)
从表3中可以看到,与BP神经网络模型与RBF神经网络模型类似,核方法对CPI时间序列的长期预测效果并没有比ARMA模型有显著提高。同时,如前文所言,窗宽的选择是核方法的重要组成部分,从表5中可以看到,窗宽与提高比率在数值上呈现倒“U”型依赖关系,在窗宽较大或较小的两侧预测误差较大,而在8.00处左右的中心位置误差较小。下页图5所示为自2010年1月到2017年1月的实际CPI数据(实线)与采用窗宽为8.00的核方法进行预测得到的CPI数据(虚线)比较示意图。与图3相比,核方法与ARMA模型在长期预测方面有共同的缺陷,那就是对于多步之后预测值趋于常数,不能反应实际CPI的变化。这个结果是符合大多数领域长期预测准确度较差这一事实的。
(2)短期预测情形

图5 核方法真实CPI预测效果示意图(2010.1-2017.1)
用上文中的方法考虑预测训练样本数为300,预测样本数为25个的情形。这里的预测区间为2015年1月至2017年1月,属于短期预测。经过计算,预测窗宽和对应误差如表6所示。

表6 核方法预测窗宽及对应误差表(2015.1-2017.1)
从表4中可以看出,核方法的短期预测较ARMA模型有较大提高,提高比例与窗宽呈现倒“U”型的依赖关系,最大提高比例为45.10%,对应的最优窗宽是0.60。图6为对应于窗宽为0.60时2015年1月至2017年1月的实际CPI(实线)与预测CPI(虚线)走势图,从图中可以看出,相比ARMA模型(图4),核方法虽然没有对局部波动进行更加精细地刻画,但是仍然能够较好地把握CPI的变化趋势,因而减小了预测的误差,大幅提高了预测的精度。

图6 核方法真实CPI预测效果示意图(2015.1-2017.1)
3 结论与建议
CPI是国民经济运行的指示灯,本文采用ARMA模型对CPI时间序列进行拟合和预测,得到短期预测误差为3.599,长期预测误差为12.528。针对ARMA模型没有准确描绘CPI时间序列中的非线性结构问题,本文进一步采用BP网络、RBF网络和非参数方法对预测作了改进,三种方法在长期预测方面精度与ARMA模型相近。而在短期预测方面,三种方法预测精度均较ARMA模型有较大提高,最大提高比率为51.85%。
对CPI序列进行精确管理对提高经济运行效率、增进居民获得感有重要意义。本文采用的几种方法可以较为准确地对CPI序列进行预测,非参数核方法预测效果是其中比较好的一种,其计算量适中,可以方便加以运用。而对于神经网络方法,其模型构建比较简单,可复制性强,实际中应用较广泛。但是,由于不需要提供精确函数关系,神经网络模型改进手段也同时受到限制,预测效率的进一步提高存在一定难度。
