一种基于正态分布密度函数的模糊查询方法

李 雪

(南京航空航天大学 计算机科学与技术学院，江苏 南京 211100)

0 引 言

日常生活中可以见到很多模糊现象，比如有一个古老的希腊悖论是这样说的：一颗豌豆不叫一堆，两颗也不叫，这是大家都公认的，但是可不可以说10 000颗豌豆不叫一堆而10 001颗叫一堆呢？肯定不能这样定义，但是适当的界限在哪里？这是一个渐进的过程，没有明确的范围，不能用精确的数值进行描述。然而，研究者们一直忽略这些不确定性，并且所有的数据库管理系统都是基于精确的数据。直到20世纪60年代，Zadeh教授发起了关于模糊性的研究。

查询操作是数据库的重要操作之一，而现有的绝大多数查询操作都要求指定某个属性位于某个具体区间的所有记录。但是可以发现，在日常生活中，人们想要得到某种结果时，并不能很明确地表达他们的查询要求。比如某个人需要租房子，需要找到价格便宜并且离市中心近的房子，当在数据库中进行查询时，“离市中心近”以及“价格便宜”这样的查询语句就是模糊的概念。但是一般的数据库管理系统并不能对这样的模糊语句进行查询，在网络规模不断扩大的今天，数据库的查询次数以指数级别在增长，精确的查询则要求数据库的操作者对数据库中的数据有很清楚的了解，例如DBA(database administrator，数据库管理员)。这直接使得对数据库内容不熟悉的人很难去获得其想要的查询结果，其大概率查询到空的结果集或者过多的数据记录从而难以筛选。而模糊查询则为该问题提供了解决思路。然而不论是传统的关系数据库还是图数据库都只能对精确的条件进行查询，无法查询形如上文提到的“价格便宜并且离市中心近的房子”这样带有模糊语句的查询条件，因此急需一种合适有效的方法将模糊的查询条件转化成精确的查询区间，使其可以在数据库管理系统中执行。

1 相关研究工作

1.1 模糊查询

1.1.1 关系数据库模糊查询

国内外对模糊查询进行了大量研究，例如，文献[1-4]均说明了如何使用正向法和反向法对查询条件进行处理，将其转化成精确的查询区间；文献[5]定义了一种模糊数据库查询语言，它可以处理数据库中遇到的模糊的或者精确的查询条件；文献[6]设计了一个样本数据库，可以在上面进行模糊查询或者精确查询，对比传统数据库，在样本数据库上进行模糊查询的时间花费大大降低；文献[7-8]在现有关系数据库上对查询语言进行模糊扩展，同时引入了权重的概念。

1.1.2 云数据库模糊查询

关于NoSQL模糊查询，国内并没有相关研究，国际上此类研究也并不是很多。文献[9]对NoSQL图数据库的Cypher语言进行扩展得到Cypherf语言使其可以进行模糊查询；文献[10]提出了一个基于图的模糊NoSQL模型，称FNoSQL，用来处理大数据库的同时也扩展了NoSQL；文献[11]提出使用合适的工具用来在Neo4j的cypher语言中表达模糊查询，用模糊性来帮助解决模糊模式匹配。

文献[12]实现了可视化模糊查询生成器AskFuzzy，它是前端的可视化界面和后端的数据库之间的一个中间层，可以在where中基于概念而不是数据来使用模糊谓词进行查询。

文献[13-14]提出了一个可以灵活查询模糊数据库的系统SUGAR，该系统建立在Neo4j图数据库管理系统中，支持Cypher查询，由transcriptor模块和分数计算器模块组成，并且引进了Fudge语言来实施，该语言可以灵活处理模糊的或者精确的数据，可以用来处理模糊图数据库中的偏好查询。

1.2 相关理论知识

生活中经常会有很多无法用精确的数值表达的不确定性，比如人们交谈时的口语，各种形容词以及副词，各个领域主观的意见以及判断等等，这些都是模糊性表达。所有的模糊性都是一种主观的衡量，需要用隶属函数对这些模糊性进行转换，明确这些模糊性的隶属规律，找到合适的隶属函数，这样就可以在充满不确定性的现实生活中和必须使用精确数据进行计算的数学中找到一个很好的平衡点[15-16]。

1.2.1 模糊集理论

(1)模糊集。

模糊集A可以用元素x和它的隶属函数μA(x)的集合表示，其中x是论域U中的一个元素,也就是：

A={(x,μA(x))|x∈U}

一般可以通过模糊集合所对应的隶属函数来对模糊集合进行划分，因此如果知道论域U上的模糊集合，就能通过模糊集合中的元素x来确定元素x所对应的隶属函数μA(x)。

(2)α截集。

α截集可以认为是论域U中所有元素x所对应的隶属函数μA(x)的值都不小于α的一个集合：

Aα={x|μA(x)≥α, ∀x∈U}

其中，α为置信水平(阈值)。

1.2.2 正态分布

如果有随机变量X服从参数为μ,σ(σ>0)的概率分布，那就称随机变量X服从正态分布，记为X～N(μ,σ2)，它的概率密度函数表示为：

图1是一个正态分布概率密度函数。从图中可以得知，平均数周围的数的取值概率明显大于两边的，通常生活中很多的大样本数据都服从正态分布，比如学生的成绩大都比较集中，中等的偏多，成绩特别好或者特别差的人总是占少数的；人的身高在某个中等范围的占大多数，特别高的人以及特别矮的属于少数等。基于这个特点，考虑使用正态分布密度函数作为隶属函数对模糊属性进行区间匹配。

图1 正态分布密度函数

2 基于正态分布密度函数的模糊化匹配方法

传统的模糊化查询主要是采用Zadeh在1965年提出的模糊数学理论，通过对论域中不同模糊集设置相应隶属函数来计算某具体数值的隶属度，从而进行查询。然而在实际的图像数据库中，采用预设的隶属函数会面临诸多问题，如：

(1)很难对所有的模糊集都设置一个相对较为准确的隶属函数；

(2)忽视数据库中已有样本的信息利用；

(3)对数据库中节点作属性增加的代价较大；

(4)很难确定最终的匹配区间。

为了将模糊化查询应用于图形数据库，文中提出了一种基于正态分布密度函数的模糊化自动匹配方法，克服了上述问题，并结合实例作了性能分析。

设某一类节点N拥有k个实体，即：{N}={n1,n2,…,nk}。

其某个属性attr是连续的，第i个实体对应attr的值用ni.attr表示，一般地，可以预计算{N}在属性attr的均值E(N)与方差D2(N)，即

E(N,attr)=(n1.attr+n2.attr+…+nk.attr)/k

D2(N,attr)=((n1.attr-E(N,attr))2+(n2.attr-E(N,attr))2+…+(nk.attr-E(N,attr))2)/k

则假设{N}的attr属性值服从正态分布，即N.attr～N(E(N,attr),D2(N,attr))。为了简便，所有的E(N,attr))用E表示，D(N,attr)用D表示。其概率密度函数为：

由概率论可知，函数f(x)的线下面积为1，其定义域为(-∞,+∞)。

根据具体模糊集的内容对定义域进行划分。一般地，对于模糊集A其均为论域U的子集，根据具体的A可将论域进行t个划分，即：

d(U)={d1,d2,…,dt}

且A属于第s个划分，即A=ds。例如：

如果U是年龄[0,100]，可将其分为“年幼”、“年轻”、“中年”，“老年”4个划分，“年轻”为第2个划分；

如果U是考试成绩[0,100]，可将其分为“差”、“普通”、“优异”3个划分，“普通”是第2个划分。

论域的每个划分di都可以赋之一个权重wi，满足：w1+w2+…+wt=1。

为了描述方便，设所有的权重是一样的，即

wi=1/t(1≤i≤t)

给出模糊区间的定义：

若模糊集A可将论域进行t个划分，且A属于第s个划分，则A的模糊区间表示为：

farea(A)=[fmin(A),fmax(A)]

若s=1，则fmin(A)=-∞；若s=t，则fmax(A)=+∞。

若A'属于第s+1个划分，则fmax(A)=fmin(A')，且满足：

令Y=(X-E)/D，则Y服从标准正态分布：

设Φ(x)为标准正态分布的累积分布函数，即：

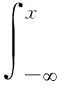
且Φ(x)在定义域R上单调递增。

则有：

若Φ(x)的反函数为Φ-1(x)，则有：

fmin(A)=Φ-1((s-1)/t)·D+E

fmax(A)=Φ-1(s/t)·D+E

一般地，函数Φ(x)的定义域为[0,+∞)，值域为[0.5,1)，且Φ(-x)=1-Φ(x)。有Φ-1(x)的定义域为[0.5,1)，值域为[0,+∞)。由Φ(-x)=1-Φ(x)，有-Φ-1(x)=Φ-1(1-x)。

所以上式可化为：

fmin(A)=

根据上式可以计算fmin(A)和fmax(A)。为了避免对“无穷”的计算操作，利用论域U=[Umin,Umax]的上下限对正负无穷进行取代，即：

fmin(A)=

对区间farea(A)进行求平均操作，即均值：

定义：

若s=(t+1)/2，则E(N,attr)为模糊集A的隶属函数的极大值点max(A)；否则，均值ave与正态分布曲线的交点的横坐标为模糊集A的隶属函数的极大值点max(A)。

若f(x)在x≥E(N,attr)区间的反函数为f-1(x)，则有：

求得模糊集A的隶属函数的极大值点max(A)。若论集U共有t个划分，其每个划分的模糊集A1,A2,…,At对应的极大值点分别为max1，max2，…，maxt。不妨令max0=Umin，maxt+1=Umax，则用正、余弦曲线描述每个模糊集的隶属函数：

若2≤i≤t-1，则

至此完成了基于正态分布的模糊集对应隶属函数的自动生成。设置阈值ε，令Ai(x)>ε，得到的不等式的解即为Ai(x)所对应模糊集的区间匹配。

3 实例分析

第二节叙述的方法可以用在很大的数据量上，利用正态分布函数直接计算出每个模糊集对应的区间匹配。为了方便起见，选择一个班的成绩作为研究对象，分别计算出成绩偏低、中等以及优秀三个模糊集的隶属函数，设置合适的ε值，得到区间匹配。

3.1 区间匹配实现一般流程

图2描述了模糊集区间匹配的一般实现过程。

图2 模糊集区间匹配的实现过程

3.2 区间匹配计算过程

(1)确定模糊集以及s,t。

由表1计算出学生成绩的平均值E≈77.6，标准差D≈15.3，方差D2≈234。将学生成绩[0,100]划分为“低”、“中等”、“优异”三个模糊区间，由此可知t=3，s取1，2，3。

表1 学生成绩

(2)计算fmin(A)、fmax(A)。

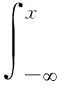
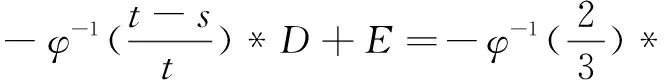
15.3+77.6≈71

当s=2时，因为若A'属于第s+1个划分，则fmax(A)=fmin(A')，所以

fmin(A)=71

当s=3时，fmin(A)=84.2，fmax(A)=+∞。

根据上式可以计算出fmin(A)和fmax(A)。

为了避免对“无穷”的计算操作，利用论域U=[Umin,Umax]的上下限对正负无穷进行取代，即

当s=1时，fmin(A)=0，fmax(A)=71；

当s=2时fmin(A)=71，fmax(A)=84.2；

当s=3时，fmin(A)=84.2，fmax(A)=100。

(3)根据fmin(A)、fmax(A)计算ave。

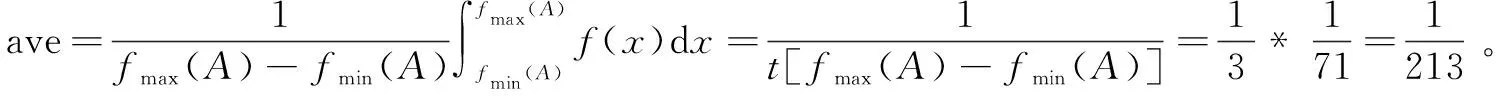
s=2时，ave=(1/3)*(1/13.2)=1/39.6。

s=3时，ave=(1/3)*(1/15.8)=1/47.40。

(4)计算模糊集的隶属函数的极大值点max(A)。

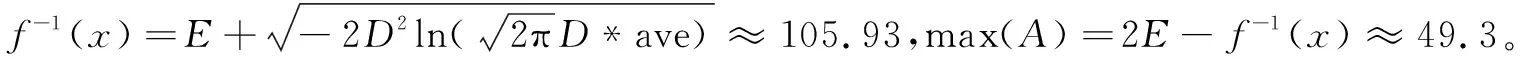
s=2时，max(A)=E(N,attr)=77.6。

s=3时，max(A)=f-1(x)=E+

(5)确定A的隶属函数。

模糊集A1、A2、A3对应的极大值点分别为max1=49.3，max2=77.6，max3=87.6，max0=Umin=0，max4=Umax=100。

A1(x)=

Ai=2(x)=

At(x)=

3.3 在不同的ε下计算区间匹配

要查找成绩优秀的学生，取ε=0.5，使A3(x)>0.5，得x的区间为[77.6,100]，查表将成绩按升序排序可知对应的结果如表2所示。

表2 ε=0.5时所得结果

取ε=0.87，使A3(x)>0.87，得x区间为[82.6,100]，查表将成绩按升序排序可知对应结果如表3所示。

表3 ε=0.87时所得结果

由上可知，ε越大，所得的结果区间越小，准确度越高。

4 结束语

以模糊集理论为基础，通过正态分布函数的密度函数的某些特性设定了一个总的模糊化自动匹配算法，可以利用样本中已有的信息对所有的模糊集都设置一个相对较为准确的隶属函数，可以通过该隶属函数对模糊集进行自动匹配，减少了用户自己设定隶属函数的主观性，大大提高了结果的准确度。该算法很大程度上增加了用户友好性，能够满足用户对模糊查询的需求，但是也存在一定的局限性。比如需要计算出所有数据的平均值和方差，数据量越大时，需要的内存越多，计算的效率会相应降低，这是今后需要改进的地方。但是当数据量越大时，数据的一般性越能体现出来，所得结果的准确度也会相应提高。