数据挖掘方法在生物实验数据上的应用

2018-09-22辛月振孙贝贝夏盛瑜

计算机技术与发展 2018年9期

辛月振，孙贝贝，夏盛瑜

(中国石油大学(华东) 计算机与通信工程学院，山东青岛 266580)

0 引言

随着大规模生物实验技术的发展和数据累积，如何处理数据，从全局和系统水平研究和分析生物学系统，揭示其发展规律已成为一个新的研究热点。传统生物数据分析方法受限于其处理能力与时间复杂度，已逐渐不适用于当前的生物数据分析。将计算机技术与生物实验相结合，采用生物信息学的思想与方法成为目前生物数据处理的新途径[1]。

近年来，机器学习方法已应用于生物数据处理。在生物数据处理领域，人工神经网络与数据挖掘算法已应用于产量的优化[2]，特别是在培养条件的优化方面。张梅等利用BP神经网络优化杜鹃花黄酮的提取工艺[3]。Khaouane L等利用神经网络和粒子群优化算法寻找最优截短侧耳素培养条件[4]。最近，随着生物数据的增加，数据分类思想也应用于生物数据处理方面[5-7]。分类的概念是在现有数据的基础上使用分类函数，或者构造一个分类模型(即通常称之为分类器)。函数或模型可以将数据库中的数据记录映射到给定的类别，它可以应用于数据预测。在文献[8]中，应用在这些实验中收集的数据，以统计方法建立数学模型来预测桑黄产黄酮产量，并取得了较好的效果。但在这个过程中，发现统计方法在处理生物实验数据具有模型建立依赖先验知识，数据受误差样本扰动大，信息易丢失等缺点。因此，文中采用分类算法对整个样本集进行高产和低产的数据分类，取得了良好的分类精度。在高产数据集的基础上，采用BP神经网络和遗传算法对产量进行优化。最终得出了最优产量与实验条件。

1 数据采集与分类

1.1 数据采集

首先从生物单因素试验中采集数据。文中所采集的实验数据来源于桑黄实验室发酵实验[9]，包括接种量、PH值、初始液量、温度、种龄、发酵时间和转速等参数。共获取了90组实验数据。

1.2 数据分类

将数据集划分为高产量数据集和低产量数据集两部分。由之前的生物数据处理经验，来自生物实验的数据具有不同实验梯度数据相似度高、实验梯度有限等特点。传统的预测方法在整个数据集中很难取得好的结果。所以文中使用分类的方法，针对高产的数据，增加分类数据集中的样本差。选择分类时必须考虑到两个关键因素。

第一，保持两个数据集之间的平衡。较大的不平衡可能导致分类器中更多的偏差[10]。类别数据不均衡是分类任务中一个典型存在的问题。简而言之，即数据集中，每个类别下的样本数目相差很大。例如，在一个二分类问题中，共有100个样本(100行数据，每一行数据为一个样本的表征)，其中80个样本属于class1，其余的20个样本属于class2，class1∶class2=80∶20=4∶1，这便属于类别不均衡。如果使用这种模型，分类器就不能找到高产因子，也不能为BP神经网络建立训练数据集。

第二，高产数据集和低产数据集必须覆盖所有单因素实验的实验条件。文中考虑两种分类策略：第一个，取黄酮类化合物产量的中位数作为分类边界(在实验数据中是1 100 μg/ml)，这样获得了数目相同的高产和低产数据集。通过大量实验，证明在此分类边界下分类效果是可以接受的。但是这种方法将会使某些单因素实验因素完全划分为某低产类或高产类当中；另一个策略是在每一组单变量实验中选择一个边界。保持每个单因素实验数据在两个不同的类中，并且尽量使两个类别中的元素数量尽可能接近。结合上述条件，选择黄酮产量为1 273 μg/ml作为边界条件。在这个边界条件下，得到20组高产量数据和30组低产量数据。

分类结果如表1所示。

表1 分类准确率(逻辑回归)

2 模型建立

BP(back propagation)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络之一[11]。

基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行[12]。

2.1 正向传递子过程

现在设节点i和节点j之间的权值为wij，节点j的阈值为bj，每个节点的输出值为xj，而每个节点的输出值是根据上层所有节点的输出值、当前节点与上一层所有节点的权值和当前节点的阈值还有激活函数来实现的。具体计算方法如下：

(1)

xj=f(Sj)

(2)

其中，f为激活函数，一般选取S型函数或者线性函数。

2.2 反向传递子过程

反向传递是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的连接强度和隐层节点与输出节点的连接强度以及阈值，误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。

假设输出层的所有结果为dj，误差函数如下：

(3)

其中，E(w,b)为当前位置的梯度。

由经验公式可以确定隐含层节点数目，如下：

(4)

其中，h为隐含层节点数目；m为输入层节点数目；n为输出层节点数目；a为1-10之间的调节常数。经过反复试验确定中间层节点数为9。

每个隐层传递函数设置为“tansig”(双极性S函数)、“logsig”(单极性S函数)。训练方法设定为“trainlm”。trainlm是指L-M优化算法[13]。

Sigmod函数如下：

(5)

每次选择15组数据进行建模，选择5组数据进行验证。训练次数设定为1 000，训练收敛误差设定为0.000 01。重复7次实验的结果如表2所示。平均误差为133.53，误差百分比为8.7%。误差值如图1所示，误差百分比如图2所示。可以判断模型取得了很好的效果。

表2 BP预测结果

图1 误差值

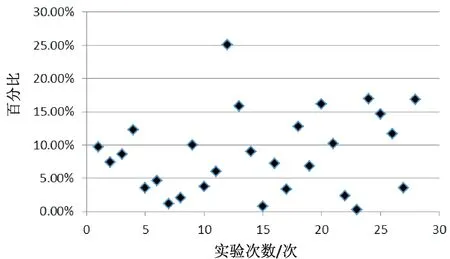
图2 误差百分比

3 实验仿真与寻优

文中采用遗传算法(genetic algorithm，GA)来优化产量。GA是模拟达尔文生物进化论中自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法[14]。GA是从代表问题可能潜在的解集的一个种群(population)开始，而一个种群则由经过基因(gene)编码的一定数目个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现(即基因型)是某种基因组合，决定了个体的形状的外部表现[15]。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，往往进行简化，如二进制编码。遗传算法过程如图3所示。

图3 遗传算法流程

设置GA算法的参数如下：种群大小设置为300，染色体大小设置为6，交叉速率设置为1，变异率设置为0.01。提取BP神经网络的隐藏阈值作为GA算法的适应度函数。在大约30到500次迭代之后，GA过程返回最佳个体。训练过程如图3所示。重复测试7次，结果如表3所示。可以看到，得到的收益比实际收益略有增加。