近似完全匹配层边界条件吸收效果分析及衰减函数的改进

罗玉钦 刘 财

(吉林大学地球探测科学与技术学院，吉林长春 130021)

1 引言

为了消除正演模拟中边界反射，需要引入吸收边界条件。Berenger[1]在研究麦克斯韦方程时提出了完全匹配层(PML)边界条件，是目前吸收效果最好的边界条件。在地震波场模拟中，最早采用的是分裂PML边界条件。Chew等[2]和Collino等[3]对PML边界条件进行了一般性地推导，将其解释为复坐标伸展变换的结果；Chew等[4]和Hastings等[5]首先将PML边界条件引入地震波模拟。Komatitsch等[6]将该方法推广到二阶弹性波方程中，但需更大的存储量并且降低了计算效率，因此发展了非分裂PML边界条件，但如何计算或者避开卷积项一直是研究重点。Drossaert等[7]采用递归积分的方法避开卷积项；Cummer[8]提出了近似PML(Nearly PML，NPML)边界条件；NPML边界条件应用了波场变换，既不改变波场形式，也不需要进行卷积处理，很快就被推广到声波介质、弹性介质和双相介质的地震波模拟[9-11]。但当波近平行入射PML边界时，衰减系数会变得很小，无法吸收大角度入射波和瞬逝波。Kuzouglu等[12]提出了复频移技术(CFS)，将进入PML区域的地震波传播方向向法线方向弯曲，增强了对大角度入射波的吸收。Roden等[13]提出了基于CFS的卷积完全匹配层(C-PML)边界条件；Komatitsch等[14]将C-PML边界条件推广到弹性介质。近年来，中国学者也对完全匹配层做了许多研究[15-22]，王守东[23]给出了声波模拟中PML边界条件的基本原理；秦臻等[24]使用辅助变量推导了微分形式下的PML边界条件，在此基础上，熊章强等[25]采用CFS技术提出了辅助微分方程完全匹配层边界条件。

在完全匹配层中，衰减因子占有十分重要的地位，决定着匹配层的吸收能力。Collino等[26]提出了与内边界距离呈指数关系的衰减函数，后经Groby等[27]改进整理，一直沿用至今。陈可洋[28]指出指数衰减函数随着阶数的变化，在内边界处过于平缓或者剧烈，不利于波的传入，并提出了正弦型和余弦型衰减函数，但效果有限。理论上指数型和正余弦型衰减函数都能完全吸收入射波，但离散之后，反射是由每一层的变化差以及整体边界层的反射系数共同决定，因此要进一步提升匹配层的吸收能力则十分困难。为此，本文设计一种更为灵活且能够控制衰减因子在各层增速的衰减函数，在不增加PML层数且不减小衰减因子最大值的情况下，压制离散差异带来的虚假反射，提升边界的吸收能力。

2 理论

2.1 近似完全匹配层边界条件

本文基于速度—应力方程组采用时间二阶、空间十二阶的交错网格有限差分法进行正演模拟。二维频率域一阶弹性波动方程为

(1)

式中：ω是圆频率；λ、μ是拉梅常数；ρ是密度；Vx、Vz为频率域弹性波场速度分量；Txx、Tzz、Txz为频率域弹性波场应力分量。复坐标伸展变换(CCS)的形式为

(2)

有

(3)

式中α是衰减函数。将式(3)代入式(1)，可得复坐标伸展变换后的方程组

(4)

然后将上式进行分裂，将应力与速度分裂为x方向和z方向分量，并转换到时间域，得到在PML计算区域波场迅速衰减的方程组

(5a)

(5b)

(5c)

(5d)

(5e)

式中：上标“x”、“z”分别为波场沿x和z方向的分解量；vx、vz为时间域弹性波场速度分量；τxx、τzz、τxz为时间域弹性波场应力分量。式(5)即为最早经典的分裂PML边界条件。该方法将五个变量分解为十个，方程的数量也为原来的两倍，计算效率低，占用存储空间大。而近似完全匹配层是对式(4)进行变换，有

(6a)

(6b)

(7)

(8)

对其他变量采取相同的方法并变换到时间域中，有

(9)

式中

(10)

式(9)即为时间域中基于近似完全匹配层的波动方程。对比式(9)与式(5)，二者形式一致，但前者不需采取分裂的方式实现完全匹配层，只需要引入8个辅助变量来替换原主控方程中的变量，而且这8个辅助变量可通过式(10)的微分方程求取。在程序编写时不必改动原代码，实现简单。对于这种不需要改变方程形式的完全匹配层也就十分容易推广到其他复杂介质。而分裂完全匹配层需将变量分裂为两个或者多个分量并改变方程形式，实现起来十分复杂且计算效率低的缺点被放大。

2.2 吸收机理及衰减因子研究

采用复坐标伸展变换之后转换到时间域中的波动方程的解(以x方向为例)为

(11)

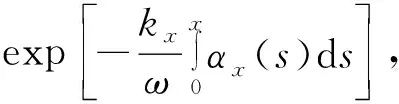
(12)

式中：L为完全匹配层的厚度；R为理论边界反射系数；vP为纵波速度；l为PML区计算点与内部边界的距离。Groby等[27]改进的衰减函数为

(13)

式(13)是式(12)的拓展，当n=2时二者等价。当取n=1时式(13)是线性函数，在内边界处的衰减梯度较大，易产生边界反射。当n值增加时内边界衰减因子变化缓慢、在外边界处迅速增加，也不利于反射的吸收。陈可洋[28]提出的正弦型和余弦型衰减函数提升了内边界处的增速，抑制了外边界处的突变。余弦型衰减函数为

(14)

正弦型衰减函数为

(15)

式中B为衰减幅度因子。B值不宜过大，否则阻碍了波从内计算区域传播到PML区域。

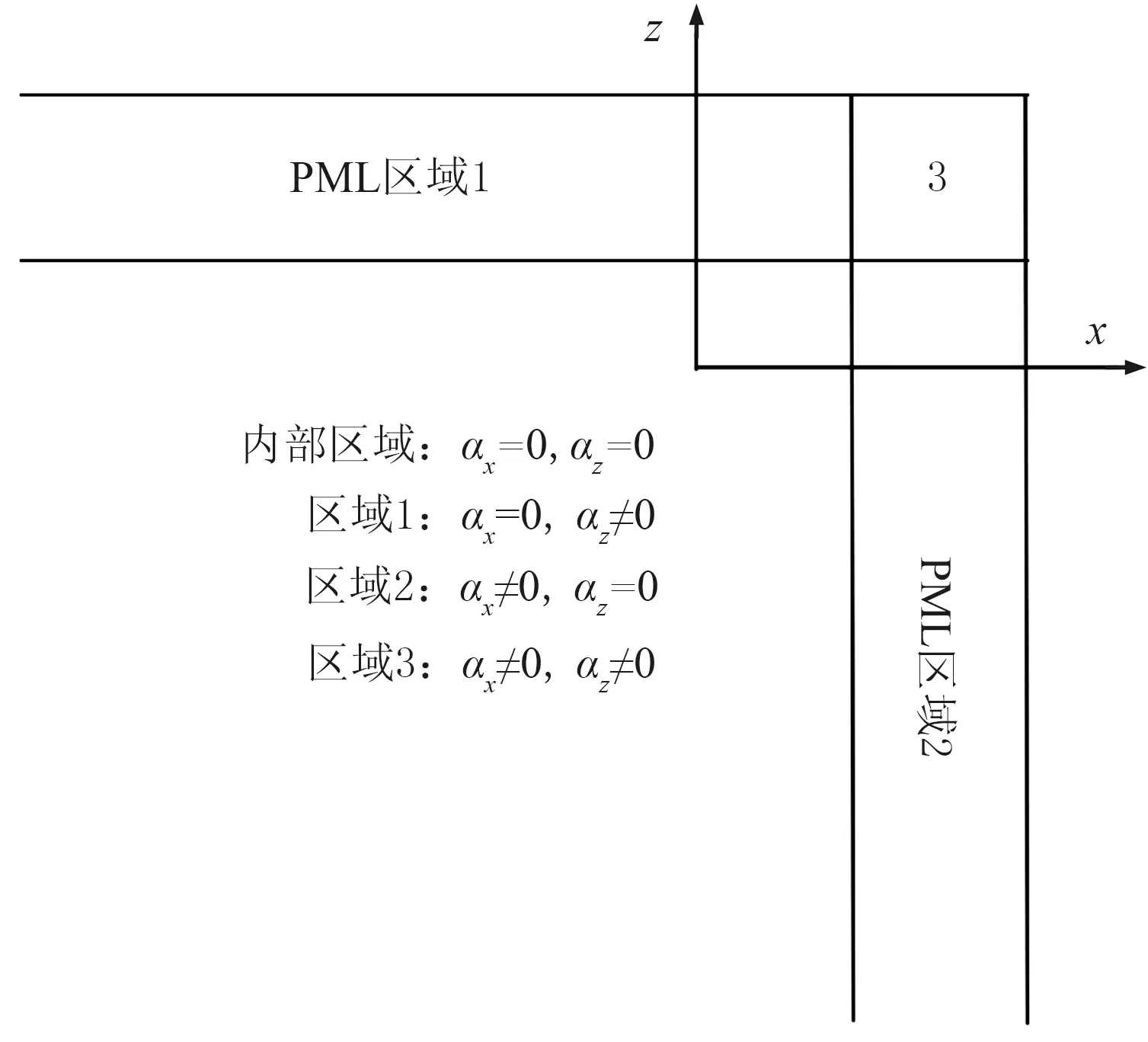
图1 衰减因子PML区域示意图

图2为指数型衰减函数和余弦型衰减函数曲线及其梯度曲线的对比。由图可见：①在相同的匹配层层数情况下，随着n的增加，指数型衰减因子在内边界处变小，在外边界附近增长剧烈。②余弦型衰减函数在内边界处的增加速度介于n=1与n=2指数型衰减因子之间。在内边界处，余弦型函数的增速较快，在外边界处增速较慢。③对于指数型函数通过增加n的值使内边界与计算区域接合更好，但在末端突变较大。④当匹配层层数缩减时，如果保持衰减函数的系数不变，余弦型衰减函数最大值是不变的，这样余弦型函数的梯度整体增加，层与层之间的离散差异增大。⑤对于指数型衰减函数，随着层数的减少，由于分母L存在，α0的最大值是增大的，使指数型函数离散差异变得更为剧烈。

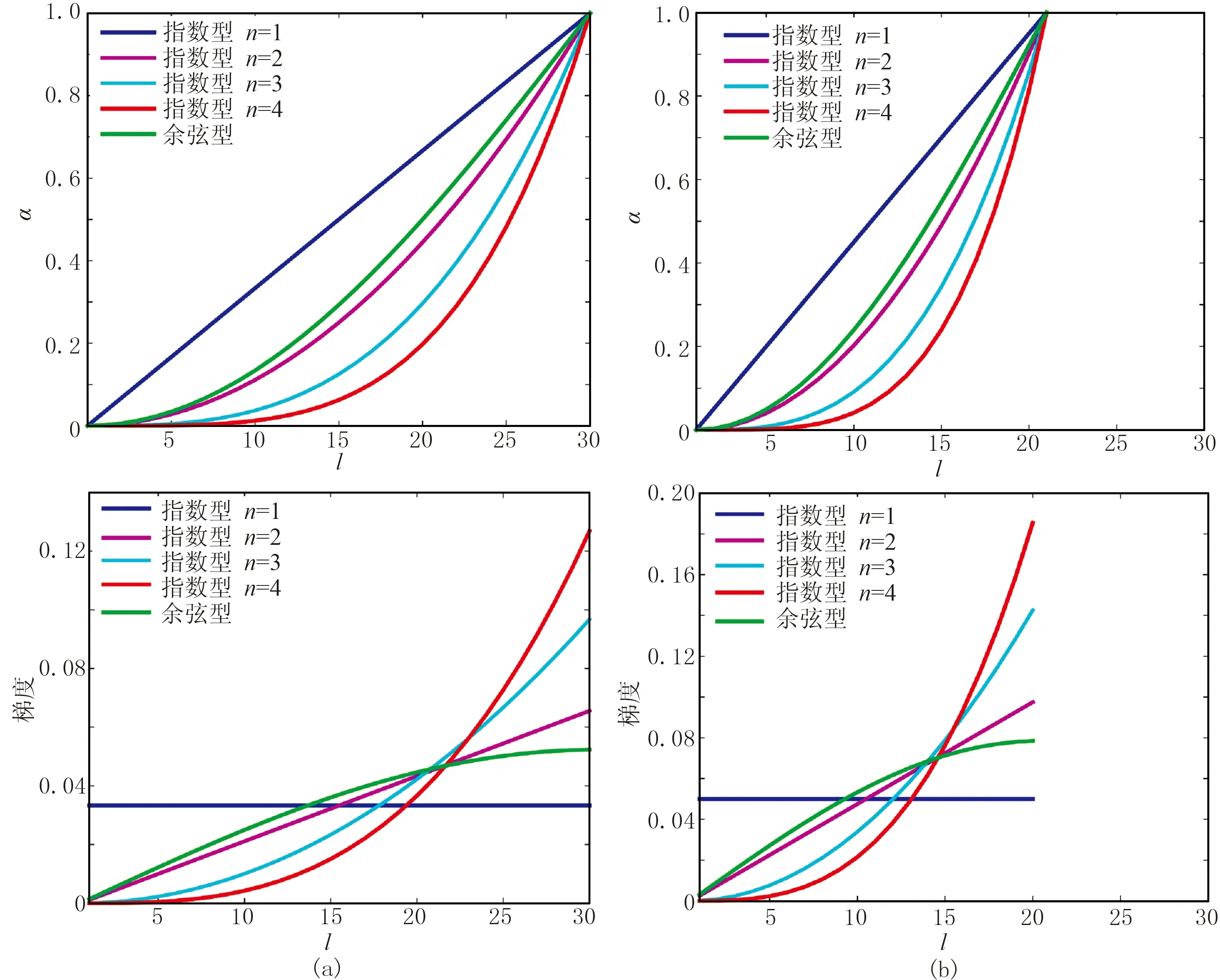
图2 L=30(a)和L=20(b)的衰减因子曲线(上)、衰减梯度曲线(下)对比

为了更为灵活地控制衰减因子在各层的增速，需要找到一个函数作为修正项，要求该函数的梯度值先增加再减小并且能够根据系数的改变控制其最大值的分布，以便控制衰减函数在各部分的梯度值。再将这个修正函数与原指数衰减函数相结合，可得修正后的指数型衰减函数

α(x)=K[β(l/L)n+γexp(-Lδ/l)]

(16)

上式第一部分β(l/L)n使该函数满足完全匹配层中衰减函数的要求，第二部分γexp(-Lδ/l)作为修正函数控制衰减函数在各完全匹配层之间的变化调整，其中K、γ、β和δ是可调整的系数。如图3所示，该修正函数通过改变δ的值控制着梯度最大点的位置，δ值越小，最大值点越接近内边界，且最大值越大。这样的特性能够很好地提升衰减梯度过小处的增速，特别是对衰减函数接近内边界区域的控制。当δ的值不变，改变γ值，γ值越大，梯度最大值越大，以此控制梯度的最大值。该修正函数不用担心外边界处的增速过大，因为在外边界处其梯度都是减小的，正好起到了压制衰减函数在外边界处增速过快的效果。基于这样的特性，将修正函数与传统的指数型衰减函数或者余弦衰减函数相加，适当地对衰减因子做出细微的改变，以达到更好的吸收效果。

修正后衰减函数依旧保留了指数衰减函数的特点(图4)，n越大，内边界因子值增速越小，而外边界处变化剧烈。在n=2时，其梯度曲线不再是一条直线。当增大β值时，衰减函数值整体随之增加(图5)，与增大衰减函数α0的值效果相同。当增大γ值时(图6)，衰减因子梯度值在匹配层中间部分得到提升，其位置还与δ的值有关。在外边界附近，无论β值与γ值如何取值，梯度在外边界处都有收缩的趋势(图7)，与传统衰减函数相比，一定程度地压制了衰减因子在边界处的增速。

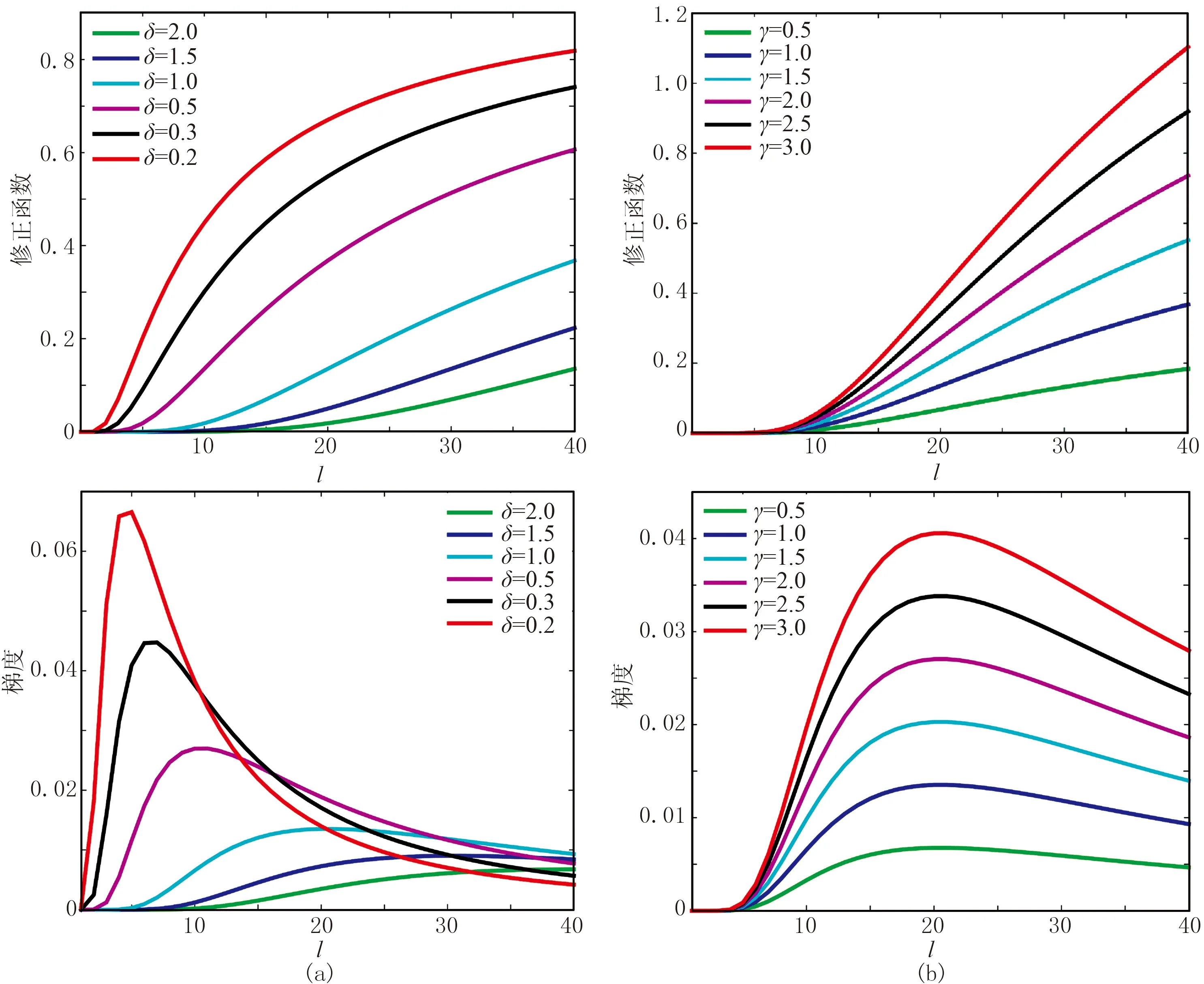
图3 不同参数时的修正函数曲线(上)及其梯度曲线(下)对比

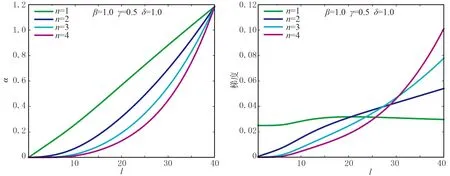
图4 n变化、其他参数不变时修正后的衰减函数曲线(左)及其梯度曲线(右)

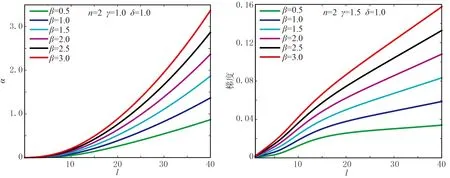
图5 β变化、其他参数不变时修正后的衰减函数曲线(左)及其梯度曲线(右)

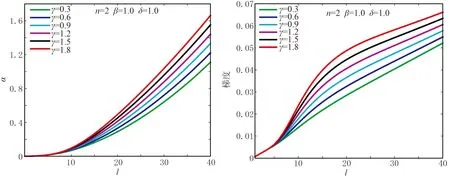
图6 γ变化、其他参数不变时修正后的衰减函数曲线(左)及其梯度曲线(右)

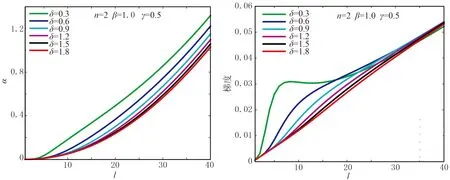
图7 δ变化、其他参数不变时修正后的衰减函数曲线(左)及其梯度曲线(右)

3 数值模拟分析

本文采用交错网格有限差分进行正演模拟，时间步长为1ms，震源是主频为25Hz的雷克子波。模型尺寸为2000m×2000m(不包括边界厚度)，两个方向网格步长均为10m，纵波速度为3000m/s，横波速度为1400m/s，密度为2000kg/m3，PML层数L分别设为5、10、15和20，纯纵波震源加载于(1000m，1000m)处。R取为10-6，余弦衰减函数中的B值取220。为了方便与指数型衰减函数做比较，将修正后的函数与指数型衰减函数取相同的系数。令

(17)

依次改变γ和δ的值以及完全匹配层层数，分析其对边界吸收效果的影响。同时将修正函数加入余弦衰减函数

(18)

当层数取5、10、15和20的时候，记录不同系数情况下的边界反射的振幅，以衡量PML边界的吸收效果。

图8是时间采样间隔为1ms、γ的取值范围为0～0.08、δ的取值范围为0～0.16时应力τxx的边界反射振幅，可见： ①当γ为零时，显示的是没有经过修正的传统衰减函数下的边界反射波振幅，此时的反射波能量很大；边界反射振幅随着γ值的增加先减小后增大，在某一个范围内吸收效果最好，而该范围会随着PML层数的改变而移动。②无论指数型衰减函数还是余弦型衰减函数，随着匹配层层数的增加，吸收效果最好区间的δ值先增加再减小，而γ值在余弦型函数中逐渐减小，在指数型函数中先增加再降低。③如图2所示，因为衰减函数最大值是不变的，层数越少，衰减因子在内边界以外的区域增长越快，两点之间的离散差异变大。而修正函数能够提升衰减因子在内边界处的增速，缩小其他区域的离散差异。因此当层数为5时，吸收效果最好的点都在δ=0的位置。④当层数增加时，新的衰减函数通过增加δ值和减小γ值降低内边界处的提升速度，并使修正函数梯度最大值远离内边界区域，提高匹配层中间位置梯度值。使衰减梯度值合理分布，以此达到更好的吸收效果。⑤当取20层时，由于离散差异引起的误差反射十分微弱，需要修正的强度也随之减弱，因此γ取值在20层时是最小的。

图9给出了在不同层数、不同衰减函数下地震波在0.5s时的vx分量波场快照。由图可见余弦型衰减函数比指数型衰减函数的吸收效果要好一些，修正余弦衰减函数和修正指数型衰减函数吸收效果更好。

为了更清晰地分析边界的衰减效果，给出了模型整体区间的能量随时间变化曲线(图10)。由图10可见，地震波在0.34s左右到达边界位置，然后迅速衰减，因此能量曲线在这一时刻骤降。残余的反射波返回计算区域，能量已经得到很大程度的削弱，当时间为1s左右时，反射波再次到达边界处，能量再次被吸收，几乎将能量吸收完全。对于余弦衰减函数，当层数较少时出现了吸收不稳定现象，吸收能力较弱，而指数型衰减函数没有此现象。就能量衰减情况来看，当PML层数为10和15时，余弦型衰减函数的吸收效果优于指数型衰减函数。当PML层数为20时两种边界条件吸收效果相当。由图中虚线所示的衰减函数修正后的能量衰减曲线可见，无论PML层数为多少，吸收效果都得到了极大的改进，其对应的δ和γ的取值为图8中吸收效果最佳点。

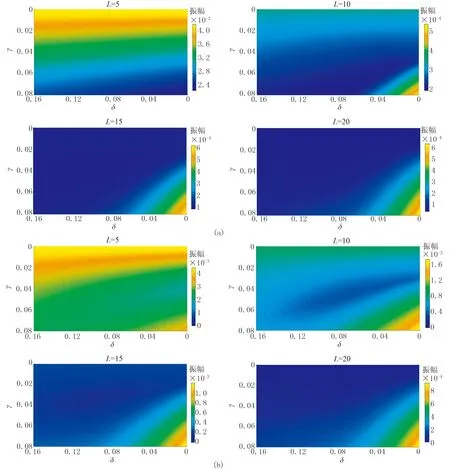
图8 余弦型(a)和指数型(b)衰减因子的吸收效果分析

图9 应用不同衰减因子PML边界条件的0.5s时刻波场vx分量模拟快照

对比(1000m，300m)处使用不同衰减函数下的应力τxx分量地震模拟记录，并求取使用传统衰减函数与修正衰减函数模拟记录τxx分量的差值曲线(图11)。对于传统的衰减函数，余弦型的吸收效果较好，只是当PML层数较少时在0.9s时接收到了十分强烈的虚假反射。差值曲线多分布于正半轴，且值较大，表明修正衰减函数压制虚假反射的效果十分明显。采用修正衰减函数PML边界条件的边界反射振幅最弱，PML层数越少，压制效果越明显，这是因为层数的增加减弱了离散差异带来的误差。为对修正之后压制效果进行定量描述，计算各系数组下修正衰减函数与传统衰减函数的边界反射振幅比，使其归一化，结果如图12所示。当γ=0时为传统衰减函数下的反射强度且值为100%，随着γ的增大，在20层时比值减小了20%，随着PML层数的减小比值甚至能够减小60%，不到原来的一半。

图10 应用不同衰减因子PML边界条件的能量衰减曲线

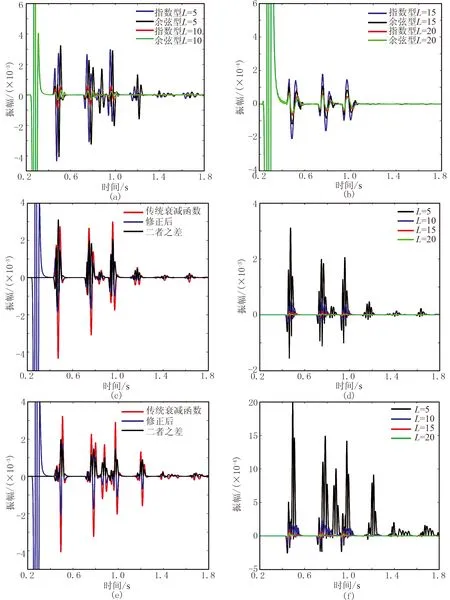
图11 使用不同衰减函数PML边界条件的(1000m，300m)处振动曲线以及差值曲线对比

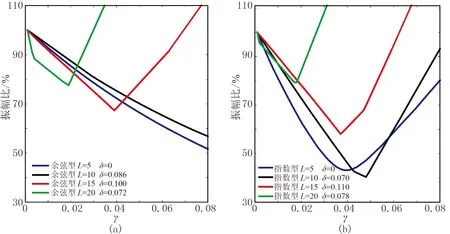
图12 不同类型衰减函数的修正前、后边界反射振幅比曲线

4 结束语

本文在理论吸收系数不变以及固定的PML层数情况下，针对离散差异所导致的误差，设计了合理修正函数，使修正后的衰减函数在层数少时增加内边界处衰减函数的梯度值，减小在外边界处的负担，在层数较多时又能减小在内边界处的梯度值并将梯度最大值外移，使梯度值在各部分合理分布。正演模拟结果显示，修正后的衰减函数大大提升了PML边界的吸收能力。