深度域高精度井震动态匹配方法

罗红梅 王长江 刘书会 穆 星 张志敬② 郑文召

(①中国石化胜利油田分公司勘探开发研究院，山东东营 257015； ②中国石化胜利油田分公司博士后工作站，山东东营 257015)

1 引言

利用叠前深度偏移方法得到的深度域地震资料具有其独特的优势，无需时深转换就可以与钻井深度对应，直接进行构造解释与构造成图。叠前深度偏移技术是目前国际上公认的解决复杂构造成像问题的有效途径[1-4]。深度域成像技术将地震成像、模型模拟和解释融于一体，成像结果为深度剖面。随着逆时偏移方法的发展，其成像点与地质模型绕射点位置完全一致，成像位置准确[5-9]。因此，它具有时间域成像不可比拟的优势。但目前深度域地震资料在油田勘探开发中的应用并不广泛，其主要原因之一是地震深度与实际深度之间存在一定的误差，从浅层到深层误差变化较大，且有正有负。误差究竟与哪些因素有关？其分布特征如何？如何将其用于深度域地震资料的校正？

目前国内外对深度域地震资料处理及速度建模方面的研究较多，而深度域资料解释应用方面的较少，深度域井震匹配、误差校正等技术尚不成熟，也是造成深度域地震资料应用具有较大局限性的重要原因之一。近年来，为减少井震误差，针对高成熟探区地震数据处理，在技术上不断探索各向异性地震数据处理方法，各向异性高斯束叠前深度偏移、各向异性逆时偏移等逐渐成为目前研究的热点[10-12]，但由于速度拾取不准确等问题造成偏移深度与实际地层深度仍然不符。研究者探讨了井震标定的适用性、深度域的深度校正问题[13-16]。林伯香等[17]、何惺华[18]、张雪健等[19]、王永刚等[20]对深度域的子波、褶积和Fourier变换等基本问题进行探讨并提出深度域合成地震记录制作方法； 胡中平等[21]提出伪深度变换方法，解决了深度域中子波随深度变化的问题； 刘斌[22]采用多尺度分析方法对合成地震道与井旁道进行分解后，利用最小平方法求取匹配滤波因子，实现时深两域的井震匹配。但是，如何确定井震深度误差并对其合理校正、实现井震高精度匹配，是当前发挥深度域地震资料优势、直接描述构造特征与地质体分布的关键。

理论上，经过精确深度偏移得到的深度域地震资料在构造形态上应该与实际构造的空间形态一致，此时如果测井资料也是准确的，两者就可以实现完全匹配。由于地震资料与测井资料的形成机理不同，使用频带不同，两者不可能在各个方面都完全一致。由于地下结构的复杂性与成像速度的相对不准确，以及地震波传播过程的复杂性与成像模型的相对简单之间的矛盾，地震成像结果总是或多或少与地下的实际情况存在差异。实际上，以前时间偏移得到的时间域地震数据与测井资料也存在深度(时间)不一致的问题。只是由于地震数据是在时间域呈现出来的，没有与测井资料在深度域直接匹配，所以两者的不一致没有凸现出来。目前深度域地震数据越来越多，已经无法回避这一问题。

针对时间序列的相似程度，生物、金融及图像分析等领域提出了动态时间规整(Dynamic Time Warping，DTW)方法，用于分析时间信号之间的匹配关系[23-25]。受此启发，本文以井震误差分析为基础，提出了一种基于动态深度规整(Dynamic Depth Warping，DDW)算法的高精度井震匹配方法。通过分析深度域井旁地震道与合成记录道之间的相似性，利用递推规划算法综合计算样点的波形幅度、波数等距离参数特征，确定二者之间的对应关系，并求取各小层内同相轴与实际深度的深度偏差,得到井旁地震道数据的偏差校正量。最后用理论数据和实际数据验证本文方法的合理性和有效性。

2 方法原理及实现

由于深度域地震资料处理过程中速度背景差异等因素的影响，地震层位反射同相轴深度与实际测井深度存在较大的误差，需要通过深度域合成记录来确定地震反射轴与测井界面的对应关系。另外，鉴于深度域子波的“空变”特性，不同层位深度域子波是不同的，单界面的子波可以直接提取，而对于多界面的地层，如果每个界面都提取各自的子波，深度域褶积会变得很复杂。如果忽略深度域子波的物理含义，寻找一个深度域的所谓算子(或称为等效子波)代替子波，依然可以使用“褶积模型”在深度域进行合成记录制作。从深度域和波数域入手，首先保持地下深度反射系数均匀采样，根据测井曲线上两个深度采样点之间的速度将子波转换到深度域，寻找一个等效子波，使其具有深度域各速度下子波的特征，然后可以用时间域褶积方法得到深度域合成记录。

为了更好地将地震层位与测井深度相对应，本文提出一种基于DDW的高精度井震匹配算法，该算法能够刻画信号的局部拉伸或压缩关系，通过寻找地震信号与测井合成记录之间的最优匹配，即可得到二者之间的深度误差校正量，实现对深度域地震信号的深度校正。

2.1 DDW方法原理

将深度域地震信号(图1a)和深度域合成记录信号(图1b)按同一间隔均匀采样，其中地震信号序列定义为R(i)(i=1,2,…,N)，R(i)为每个采样点的振幅值，该序列长度为N。测井合成地震信号定义为S(j)(j=1,2,…,M)，S(j)为每个采样点的振幅值，其长度为M。定义D(i,j)为R(i)与S(j)的振幅值之差，即两帧信号采样点之间的距离，表示为

D(i,j)=|R(i)-S(j)|

(1)

把地震信号序列作为x坐标轴，即x轴坐标为1、2、…、N；把合成地震记录信号作为y坐标轴，即y轴坐标为1、2、…、M。这样构成一个二维网格(图1)。二维网格中的交会点为地震信号某个深度与实际测井某个深度的交会点，显然地震深度与测井深度并非严格对应，存在位置偏差，地震深度局部存在拉伸或压缩现象。每个地震深度点应有一个相应的测井深度点相对应，定义第一个对应点为w1,第二个点为w2，直到最后一个深度点wk，这样{w1，w2，…，wk}构成一条路径，该路径反映了地震信号在

图1 DDW方法原理与实现过程

每个深度点对应的测井(实际)深度点。由于对应过程中可能会存在一个点与多个点对应的情况，因此路径中的k值大于等于M与N的最大值。如何找到一个最佳路径实现地震深度与测井深度的高精度匹配，是下一步需要研究的问题。

首先计算地震信号与合成记录信号这两个序列中每个采样点之间的距离，即相似度。振幅差值越小，距离越小，二者越相似。采用基于递推的动态规划方法求出该累计距离，自最后一个匹配点开始从后向前递推，很显然，若(N,M)是一个匹配点，即地震深度N对应测井深度M，则该路径点前一个格点可能是(N-1,M)，(N-1,M-1)，(N,M-1)，找出这三个点中距离最小者即为其上一最优路径点，其累计距离公式为

TD(i,j)=D(i,j)+min{D(i-1,j)

D(i,j-1),D(i-1,j-1)}

(2)

式中： TD(i,j)为某一路径上的累计距离；D(i,j)表示两记录中相应采样点i与j的距离。从最后一点或某个确定点出发搜索，反复递推，直到到达地震深度的起始点，构建出一条累计距离最小的路径，该路径即为两信号匹配的最优路径。具体实现步骤如图2所示。

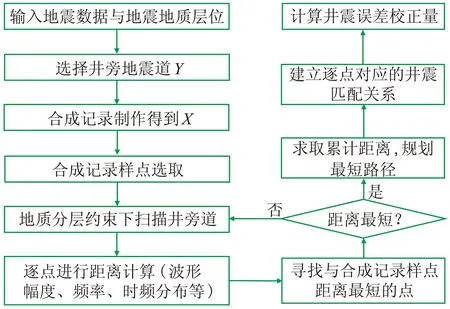
图2 DDW高精度井震匹配方法步骤

2.2 高精度井震匹配方法的建立

该动态深度匹配算法针对深度域地震信号有其特殊性，由于地震信号是多个地震反射界面的褶积，这些反射界面的真实深度与频率相关，单纯利用振幅计算距离是不全面的。因此计算距离需要同时考虑频率等参数信息。解释层位或确定性的地震深度在匹配路径规划中也需要特殊考虑，同时不同类型地质体的深度误差量板在一定程度上可以提高路径规划的效率和精度。

2.2.1 距离参数的优选

地震信号与测井合成记录信号是多套地层的褶积叠合反映，其距离也就是相似度的计算，虽以振幅值为主体，但显然以某一个采样点为中心的一定时窗内的信号频率等信息对于确定两者的相似度也是一个非常有效的参数，基于此认识，笔者提出距离为

D(i,j)=a1×|R(i)-S(j)|+

a2×|F[R(i)]-F[S(j)]|+

a3×|T[R(i)]-T[S(j)]|

(3)

式中：a1、a2、a3为加权因子；F(·)为主频；T(·)为时频。

针对式(3)中的主频项F，将地震道和合成记录道进行分频，得到低、中、高三个频率成分的信号，分别对相应频率的信号进行相似度计算。首先通过分析低频地震道与合成记录道的相似度，确定大尺度的地层旋回界面的井震匹配关系；然后针对确定的每个大尺度旋回界面之间的信号，分别在中、高频信号中逐步聚焦分析中小尺度旋回界面的对应关系，由此可大大减小距离计算的误差，提高井震匹配精度。

2.2.2 层位控制

合成记录标定是地震解释中的一个重要环节，应用深度域合成记录标定可以准确确定较大尺度旋回界面的地震反射标志层，这也是人机交互解释中重要的一步，由此将获得的地震深度与测井深度的对应关系应用到路径动态规划选取过程中，对最优路径的选取能够起到关键节点约束的作用。本文研究的方法将此确定性信息以如下方式加到路径选择中。

在距离归一化的基础上，将确定好的地震深度与测井深度对应的数据点振幅值修改为距离最大值的1000倍，这样在动态规划路径选取中基于距离最小原则，这一对振幅值的距离为零，而与其他任何一点的距离都会非常大，从而使优选的路径必须通过这一确定的深度点，可以较好地实现层位的控制。

2.2.3 误差模板的控制

由于地震信号具有典型的分形特征，有时上一套地层的信号特征与其下部的地层信号特征类似，在深度对应时可能存在误差。由于不同类型地质体、不同深度或不同构造部位导致其地震深度与测井深度误差存在一定的规律和范围，需要在路径选取中根据不同地质体误差量板建立约束控制，使路径选取限制在一定的深度范围内，这样既可避免深度对比中的误差，同时又能大幅提高路径最优选取效率和精度。

本文提出的动态深度规整井震匹配方法以距离为主体，以地震和测井合成记录信号的主频和时频曲线为辅助参数，以已知深度对应点和误差量板作为约束，建立较好的井震匹配关系，可以实现地震深度误差的高精度校正。

3 模型试算

首先设计一个单层厚5～15m、共10层的砂泥岩地层模型。每层的速度不尽相同，其中泥岩速度为2200～2900m/s，砂岩速度范围为3200～3600m/s，该模型代表真实的地下深度和地层速度；同时将该模型的砂泥岩薄互层的速度替换成统一速度3000m/s，代表在地震偏移处理阶段采用的低频速度。对两者做深度域合成记录，可以看到基于错误的低频速度进行地震处理得到的地层深度位置与实际模型存在一定偏差，在高速层信号存在压缩现象，而在低速层信号存在拉伸现象(图3)。

针对实际合成地震道与低频速度下的合成道信号，利用本文方法开展高精度井震匹配试算，采用深度动态规整算法，应用基本的距离参数(振幅信息)加上主频和时频分布等就可以实现模型地震道与井的匹配。表1为匹配得到的各样点的深度误差校正量，利用该校正量可以为地震数据的校正提供基础数据。从匹配结果可以看出，地震层位与测井层位对应关系较好，各个深度点得到归位，这两列信号的相关系数从归位匹配前的0.44提升到0.96，由此实现对低频速度模型得到的合成记录道进行深度校正，地震资料的深度误差得到较好的修正(图4)。

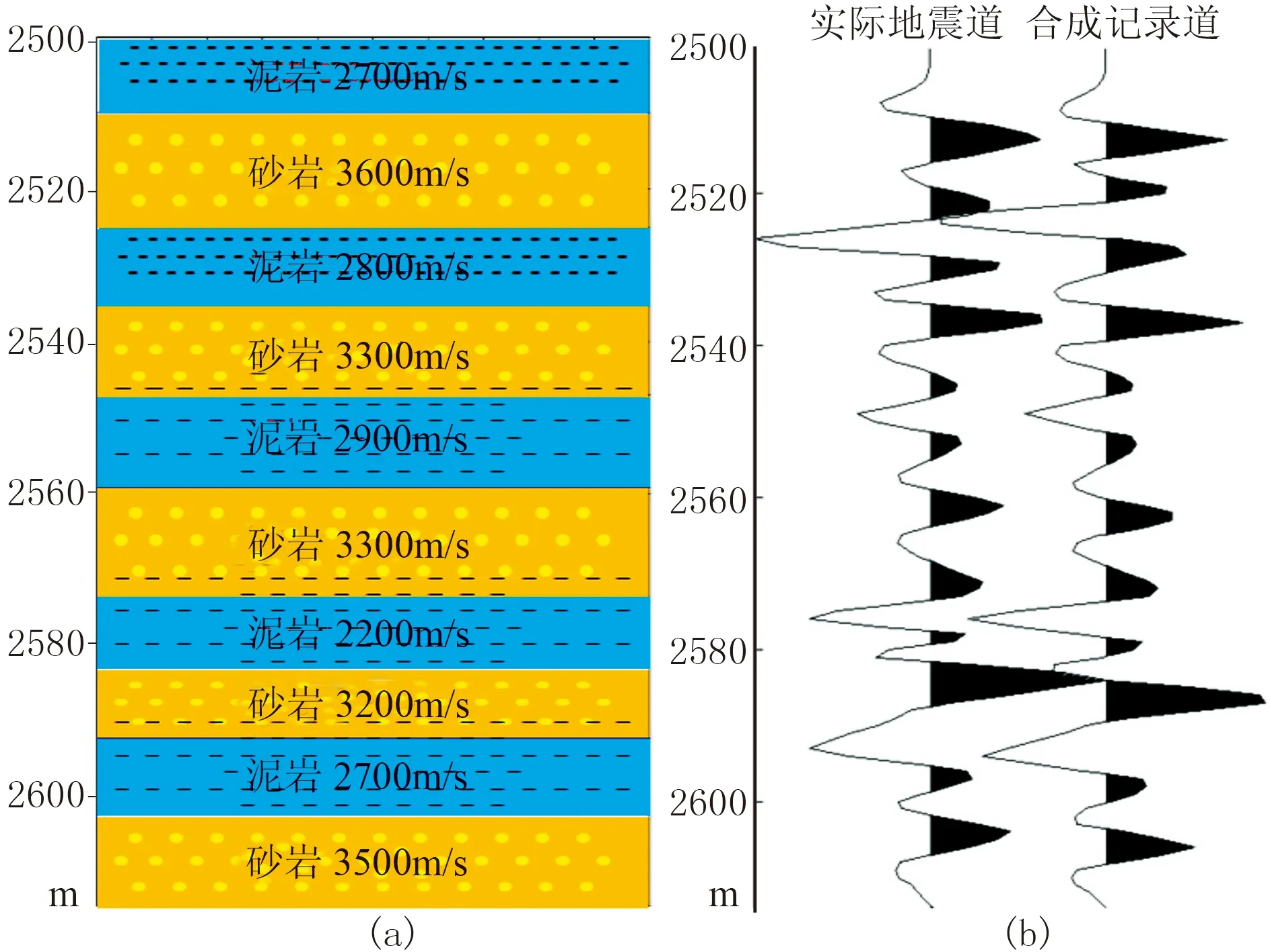
图3 砂泥岩地层模型与地震深度模型

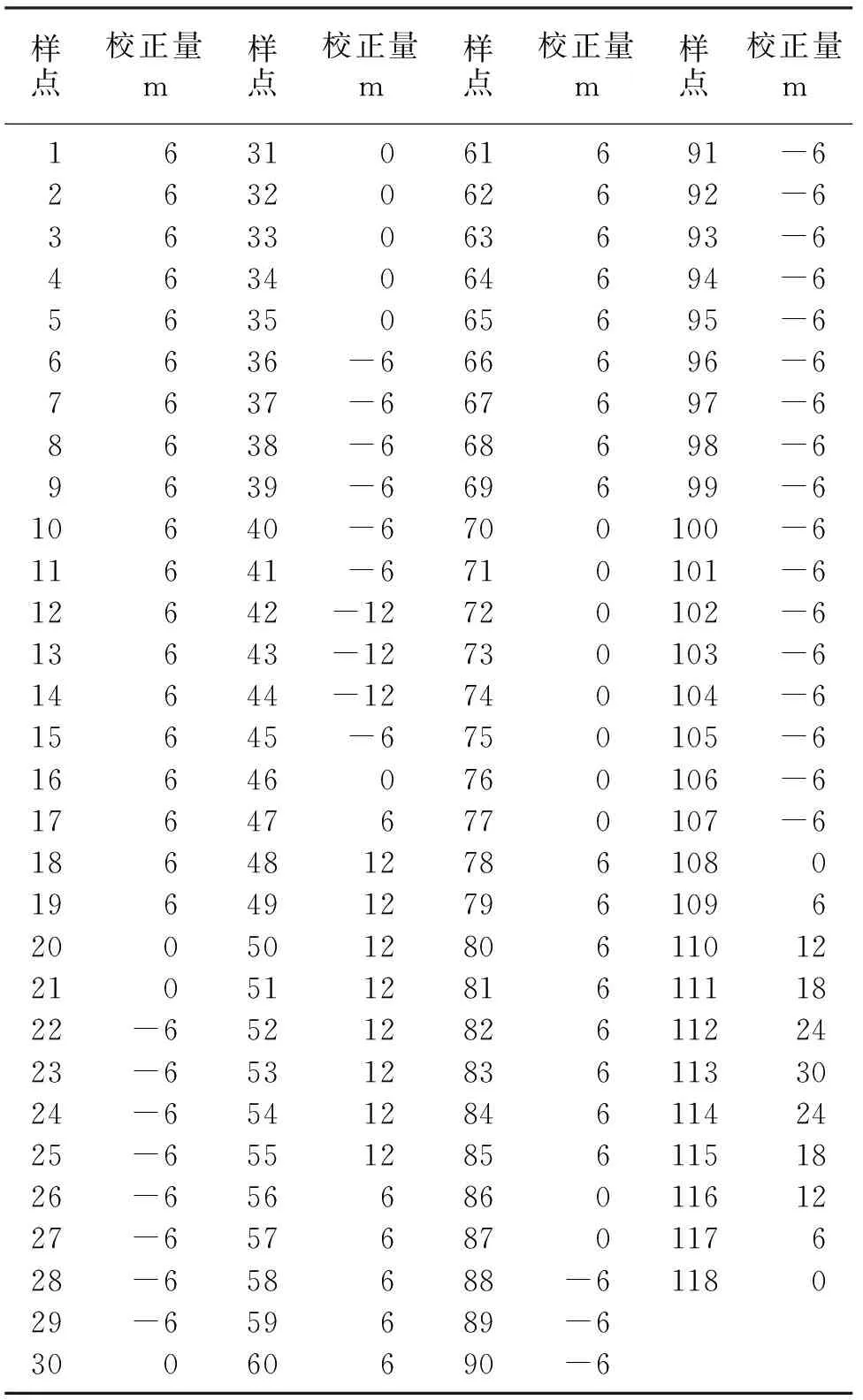
表1 DDW井震匹配后各样点误差校正量

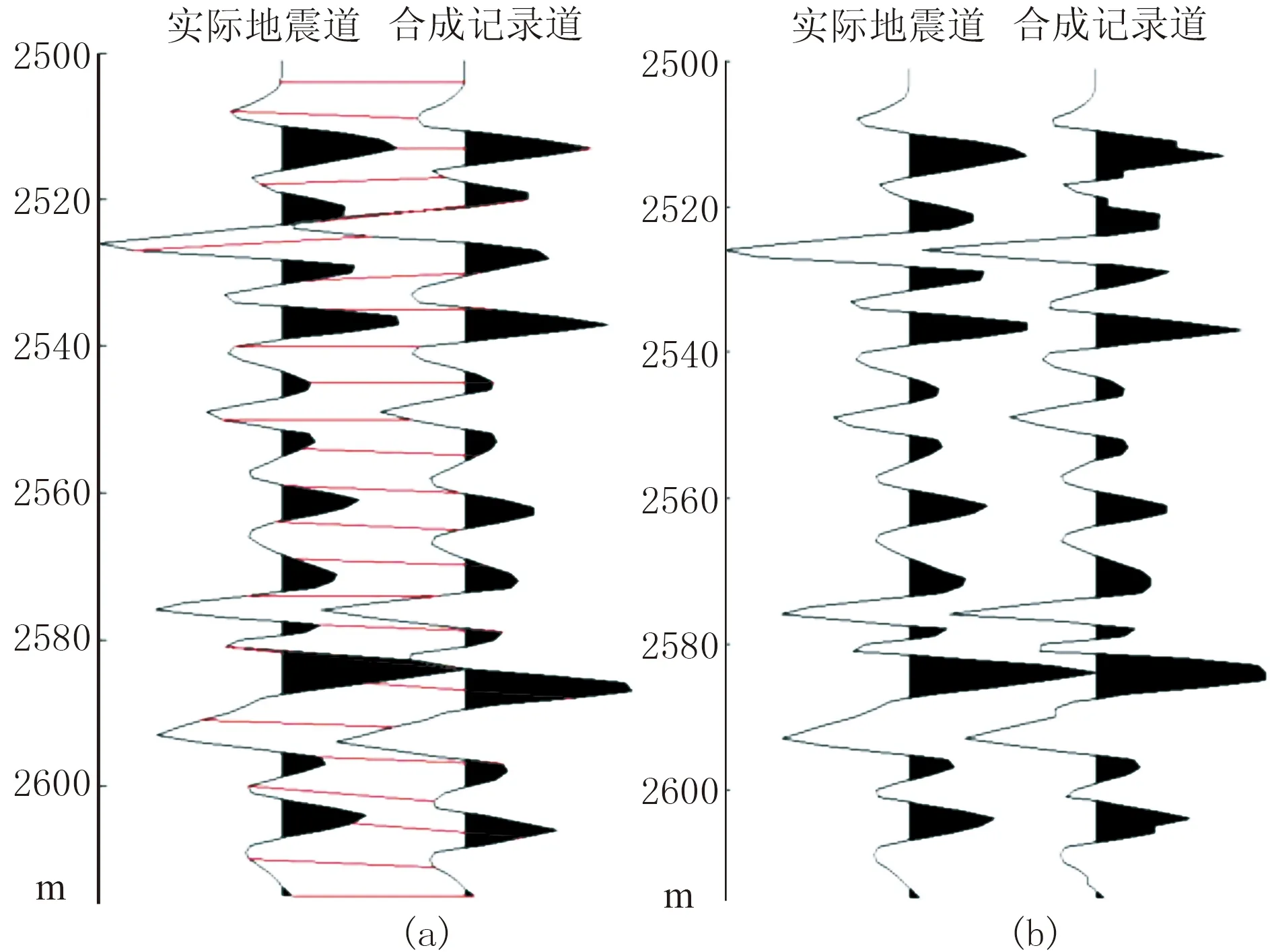
图4 实际地震道与测井合成地震记录道的匹配对比图

4 应用实例

4.1 实际井震误差分析

从实际资料出发分析地质体的井震深度误差，剖析误差分布与不同地质要素之间的关系，如埋深、产状、构造部位、地质体类型等，明晰井震误差原因，为深度域井震误差校正提供基础数据。本次研究以东营凹陷北部永安镇地区为例，系统地统计井震深度误差。该区受边界主断裂控制，具有地势陡、坡降大的特点，这种构造格局为砂砾岩扇体近物源沉积所需的碎屑物质形成及搬运提供了沉积背景。正是由于特殊沉积体的存在造成了地层速度的剧烈变化，偏移速度模型无法准确刻画这些局部变化，使地震深度与实际深度存在较大误差。

选取该区22口位于不同构造部位的井，以深度域合成记录标定为基础明确标志反射层特征，针对馆陶组底面T1、沙二段底面T3、沙三下亚段底面XT6及沙四纯上段底面T7等主要标志层，与实钻井地质分层之间进行井震误差的统计。从统计结果来看，误差绝对值具有随埋藏深度增大而逐渐增大的趋势，浅层误差相对较小，如T1层除部分钻遇断裂带比较发育的井外，井震误差均小于15m；而中深层XT6、T7误差则达到60m左右(图5a)。另外，分析误差较大的井点发现，它们大部分是位于冲积扇发育区，即当上覆地层为砂砾岩扇体时，其误差通常更大(图5b)。如永930井在3720m处进入砂砾岩体发育段，该套砾岩底面埋深为3773.0m，而地震同相轴的深度为3825.4m，比实钻深52.4m，在深度域地震剖面上砂砾岩下部层位同相轴存在明显的下拉现象。而永552井在XT6与T7钻遇细砂岩，误差则分别为28.8m和26.4m。因此，大套砾岩沉积于陡坡带的斜坡区域，沉积厚度大，横向存在很强的各向异性，误差范围在60m左右；含砾砂岩沉积于入盆区域，构造起伏平缓，沉积环境相对稳定，误差范围为40～60m；细砂岩沉积于湖盆区域，水体震荡多形成砂岩或灰砂互层，误差范围在40m以内。

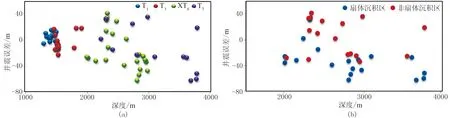
图5 永安镇地区深度域井震误差统计图

通过井震对比可以计算深度偏差。永安镇地区盐18构造区古冲沟内发育扇体，沿扇根、扇中到扇端及非扇体沉积区顺物源方向的剖面可以看出，高速砂砾岩发育的特征决定了其地震反射特征的复杂性，更造成了地震深度上的偏差。该井在砂砾岩体发育段速度变化较快，由于受地震资料在处理阶段使用的低频速度模型影响，在深度域地震剖面上真实的地层界面反射深度与实钻深度存在较大偏差。由井震误差的统计可知：永920井深部T7层位误差为27.9m，XT6层误差为-45.6m，T3层误差为-14.2m，T1层误差为7.1m； 永930井深部T7层位误差为-52.4m，XT6层误差为-34.5m，T3层误差为-6.8m。根据前述的误差定量分析，埋藏深度为1000～4000m的地震深度最大偏差为

F=A×D+B

(4)

式中：D为深度；A为误差随深度变化趋势的斜率；B为偏离该趋势的最大误差深度。

4.2 井震匹配与误差校正

以实际井的深度误差为约束，根据地震和测井合成记录信号的振幅、主频和时频信息，利用DDW方法开展实际井旁道与合成记录的高精度匹配。永920井的实际井震匹配结果表明，匹配后二者对应关系得到较大改善，局部拉伸或压缩的部分得到恢复，两信号的相关系数从匹配前的0.11提高到匹配后的0.92(图6)。根据匹配的位置信息可以得到地震资料纵向上每个反射同相轴的深度校正量。

同样将永930及永935等井进行井震匹配后可以得到相应井点的深度偏差校正量，将每口井匹配后得到的误差校正量通过克里金插值扩展到整个三维地震数据体。由于克里金插值得到的三维误差数据体并不光滑，其横向突变会引起校正后同相轴的错断，纵向突变会引起校正后波形畸变，因此必须进行一定的圆滑处理，可以得到针对研究区实际特点的误差体，将该误差体的每一样点与原始地震资料对应点的深度相加得到新的深度序列，然后进行深度数据重采样即可实现深度域地震资料的三维空间校正，得到与实际地下地层深度一致的地震剖面。与校正前相比，校正后剖面与实钻井深度高度一致，且对砂砾岩体顶面的刻画更加合理。永935井在3818m开始钻遇沙四上亚段7砂组的砂砾岩体，永930井在3720m钻遇同一套砂砾岩体，由于其速度剧烈增大，与上覆泥岩形成地震强反射。但在原始深度剖面上该强反射同相轴的深度明显与永930井相当，这与实钻情况相矛盾，而校正后的地震剖面可以合理地反映永935井砂砾岩体顶面比永930井低98m的真实情况(图7)。

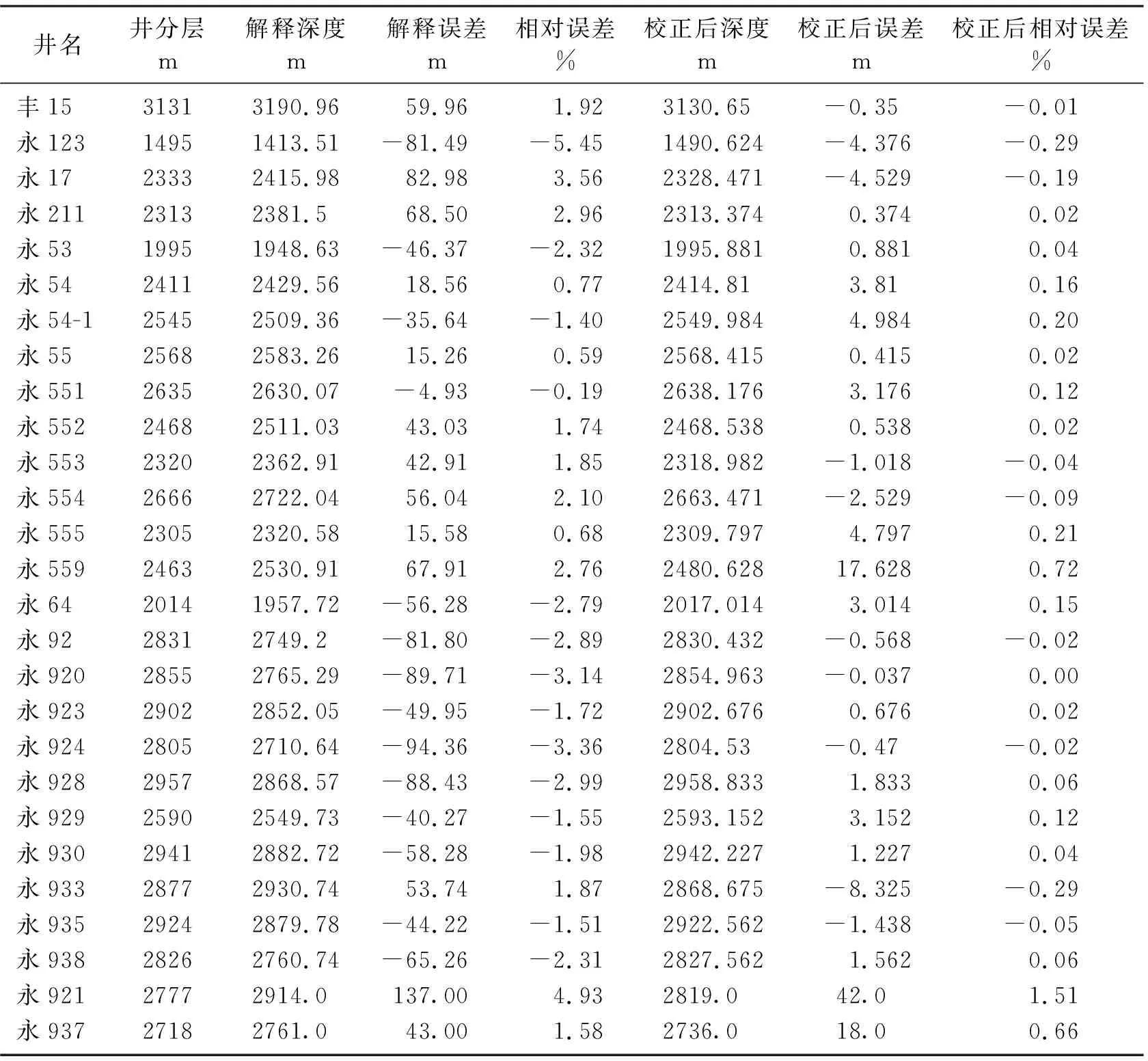
进一步对三维地震数据体开展误差校正，以该数据体为基础的构造解释更能表现平面上构造特征的实际变化。如在校正后的XT6构造图上，一方面极大地减小了构造深度误差，参与校正的26口井相对误差均小于0.3%，未参与校正的永921井和永937井相对误差均小于1.6%，都在行业标准误差允许的范围之内；另一方面，永930井处小洼陷形态和埋深发生明显改变，其西南侧小凸起校正后构造高点进一步抬升，校正前930井小洼陷与南侧洼陷在同一构造趋势线上，为北北西向，校正后受小凸起抬升影响，两洼陷间鞍部的构造深度抬升，构造趋势线发生改变，与永937井方向一致，与北部凸起边界方向吻合。永54井区的高部位构造圈闭形态改变，圈闭面积增大，该构造特征与实际地质规律更加吻合(图8，表2)。

图6 永920井合成记录与地震道的DDW高精度井震匹配

图7 永安镇地区深度域地震校正前后对比图

图8 永安镇地区深度域地震校正前(a)、后(b)XT6构造图对比

井名井分层m解释深度m解释误差m相对误差%校正后深度m校正后误差m校正后相对误差%丰1531313190.9659.96 1.92 3130.65-0.35-0.01永12314951413.51-81.49-5.45 1490.624-4.376-0.29永1723332415.9882.983.56 2328.471-4.529-0.19永21123132381.568.502.96 2313.3740.3740.02永5319951948.63-46.37-2.32 1995.8810.8810.04永5424112429.5618.560.77 2414.813.810.16永54-125452509.36-35.64-1.40 2549.9844.9840.20永5525682583.2615.260.59 2568.4150.4150.02永55126352630.07-4.93-0.19 2638.1763.1760.12永55224682511.0343.031.74 2468.5380.5380.02永55323202362.9142.911.85 2318.982-1.018-0.04永55426662722.0456.042.10 2663.471-2.529-0.09永55523052320.5815.580.68 2309.7974.7970.21永55924632530.9167.912.76 2480.62817.6280.72永6420141957.72-56.28-2.79 2017.0143.0140.15永9228312749.2-81.80-2.89 2830.432-0.568-0.02永92028552765.29-89.71-3.14 2854.963-0.0370.00永92329022852.05-49.95-1.72 2902.6760.6760.02永92428052710.64-94.36-3.36 2804.53-0.47-0.02永92829572868.57-88.43-2.99 2958.8331.8330.06永92925902549.73-40.27-1.55 2593.1523.1520.12永93029412882.72-58.28-1.98 2942.2271.2270.04永93328772930.7453.741.87 2868.675-8.325-0.29永93529242879.78-44.22-1.51 2922.562-1.438-0.05永93828262760.74-65.26-2.31 2827.5621.5620.06永92127772914.0137.004.93 2819.042.01.51永93727182761.043.001.58 2736.018.00.66

5 结论

为解决深度域地震资料与测井资料在深度上的不一致性，本文从波形相似性对比的角度出发，借助已有的井资料进行地震深度误差校正。可以得到以下几点结论。

(1)以陡坡带砂砾岩体为例，从实际资料和地质模型出发，分析井震深度误差分布特征，建立了井震误差影响因素量板。以此量板为约束，提出一种基于动态深度规整(DDW)算法的高精度井震匹配方法，实现了深度域井旁地震道与合成记录道之间的相似性分析，得到井旁地震道各小层的偏差校正量。

(2)进一步应用克里金三维插值方法将上述偏差校正量进行空间插值，建立偏差约束体，与地震数据进行运算即可得到与实钻井深度高度一致的客观合理的深度域地震数据体。

(3)本文方法既考虑了地质条件的约束，避免了人为因素的干扰，又在算法上进行了改进，使匹配精度大大提高； 同时，实现了全井段的快速匹配，对由于偏移速度误差导致能量聚焦不好而造成的地震波形变形具有较好的针对性，为开展井约束深度域反演提供井震匹配较好的地震数据。在此基础上的构造解释、地质体识别，可以极大改善复杂构造特征及地质体分布预测的效果，提高预测精度。