强容噪性随机森林算法在地震储层预测中的应用

宋建国 杨 璐 高强山 刘 炯

(①中国石油大学(华东)地球科学与技术学院，山东青岛 266580； ②海洋矿产资源评价与探测技术功能实验室，山东青岛 266071； ③中国科学院地球化学研究所月球与行星科学研究中心，贵州贵阳 550081； ④中国石化石油勘探开发研究院，北京 100083)

1 引言

综合地震、测井与地质资料进行解释与分析是油气勘探和开发过程中最基本、最重要的一种手段，也是油藏描述最基本的分析方法[1]。地震储层预测方法以地震属性数据为基础[2]，结合测井与地质信息进行储层特征参数预测[3]，可深入地研究特征参数的空间分布规律，减少地球物理反演问题的多解性，利用不同类型的资料优势，提高解释的可靠性[4-6]。

地震方法与测井方法在实际观测过程中受到各种干扰因素的影响，观测数据不可避免存在噪声，因而用于解释的数据不是完全的确定数据。地球物理各种反演方法都是建立在正演的基础上，对地下的复杂地质问题做了“模型理想化”处理，对于实际数据中的有效信号与噪声信号的界限很难有一个明确的数学关系去直接界定[7，8]，滤波等去噪方法能够一定程度的消除地震数据中噪声，但无法完全消除噪声，使用一种对地震数据噪声具有较高容忍度的储层预测方法就显得非常重要。

随机森林是Breiman[9，10]于2001年提出的一种组合预测算法，即通过组合大量决策树的预测结果作为一个整体的输出，有效地克服了单一决策树容易出现过拟合的问题。理论和实际数据的测试证明随机森林在很多领域对异常值和噪声具有很强的容忍度，克服了传统预测方法信息和知识的获取方式间接、费时且效率低下的缺点[11]。针对随机森林的容噪性，Dietterich[12]证明对训练样本的部分输出数据加入随机噪声后，Bagging方法和随机分割选择方法具有较强容噪性。Breiman通过很多不同实际类型的数据对随机森林的容噪性进行了试验，结果表明随机森林对噪声数据有很好的容忍度[13]。显然，两位专家均是对输出数据加入随机噪声，但所使用的多个输入变量是未加噪声的。其他学者在对随机森林的研究中，通过实际数据和理论推导指出了输入变量在随机森林模型占有重要的地位，并未对输入变量含有噪声时的情况进行分析[14-16]。

目前，在与储层、岩性等预测相关的方面，已有一些文献[17-20]对随机森林算法做了应用性的研究，展现了随机森林分类或回归算法的优异性能，相比神经网络算法，随机森林算法操作简单，运算效率较高[21]，与支持向量机相比，它需要设置的参数较少[22，23]。但这些文献并未对输入变量或者属性数据含有噪声时对模型影响进行专门研究。地震数据和测井数据实质上均含有噪声，即输入和输出变量均受到了噪声干扰，随机森林对于输入数据，即地震属性数据含有噪声时，容噪性如何有待研究和分析。

基于以上的研究现状，有针对性地分析随机森林算法在地震储层预测方面的容噪性显得很有必要。本文采用F3工区的实际数据研究随机森林回归算法(RRF)的容噪性。F3工区原始地震数据含有较大噪声，基于倾角导向滤波处理能够有效压制噪声，得到高信噪比数据。从含噪声的原始数据和倾角导向滤波之后的高信噪比数据中分别提取样本并建立回归模型，将这两个随机森林回归模型分别作用于原始数据和高信噪比数据，预测储层特征参数，用于对比分析。在建立随机森林回归模型和储层特征参数预测中，提取了8种不同的地震属性作为随机森林回归算法的输入变量，以孔隙度数据作为预测的特征参数，即输出变量。两个随机森林回归模型分别作用于两个数据体，计算得到4个孔隙度参数的数据体，通过已知的地质信息分析这4个数据体之间的相关性，发现样本是否含有噪声对回归模型的建立影响较大，从而对预测结果的影响也较大。用高信噪比数据建立的回归模型对预测阶段数据中的噪声具有较好的容噪性。

2 随机森林回归算法原理

决策树是构成随机森林的基础，在回归问题中，决策树为回归树，回归树的缺点主要在于容易出现过拟合，只有少量的几个数值输出，处理连续型变量问题能力局限性较大，随机森林回归算法正是为解决这些问题而提出的。

随机森林回归算法利用bootstrap技术从原始样本集随机重复抽取多个样本子集，对每个样本子集分别进行决策树建模，预测时每棵决策树均给出一个预测结果，将所有决策树输出值的平均作为森林预测值。随机森林基于统计学习理论，融合了bagging方法和随机子空间方法两大机器学习算法。

回归森林的基本方法为：

(1)Bagging思想：首先，利用bootstrap重复抽样方法从原始的训练样本中抽取k个样本子集，且每个样本子集的容量与原始训练集的一样，k个样本子集分别建立k个回归树模型，预测时对k个回归树输出值通过取平均得到回归森林输出值。该做法使每棵树的训练子集样本存在一定的重复，目的是避免随机森林的决策树产生局部最优解。

(2)随机子空间方法：在生成每棵回归树时，每个节点分裂不是考察所有可能的分割，而是每个节点随机选取部分输入变量的可能分割并找出其中的最优分割进行分裂，即随机特征选取方法。

通过重复抽样和随机特征选取两大随机方式，其构建每棵回归树的样本和构建模型的过程均存在差异，组合很多不同的回归树而形成森林，从而提高了模型的外推预测能力。Breiman通过理论和大量实际数据测试证明了随机森林算法不会轻易产生过拟合的问题，随机森林的泛化误差小于决策树的平均泛化误差，对数据中的噪声和异常值具有很好的容忍度，对噪声具有很好的稳健性。

3 测试数据分析

分别采用模拟数据和实际数据分析，说明随机森林回归算法对噪声具有很好的容忍度。

3.1 模拟数据试验

采用的模拟数据由以下非线性函数生成

y= 10sin(πx1x2)+20(x3-0.5)2+

10x4+5x5-7x6+3x7-2x8

(1)

式中x1～x8是由计算机生成的具有高斯分布的模拟数据，其样本点共计400个。对这8个变量分别加入信噪比为10∶1的高斯白噪声，其中一个变量加入噪声前、后的对比情况如图1所示。

将变量x加噪前、后数据与y值分别组成样本集，从样本中选取3/4的数据作为训练样本，1/4数据作为测试样本，利用训练样本分别建立不含噪与含噪模型，分别以加噪前、后的变量作为输入数据预测函数值，实际值与预测值对比情况如图2所示。

基于不含噪模型对不加噪数据和加噪数据进行预测，预测值与实际值的相关值分别为91.07%和92.90%。含噪模型对不加噪数据和加噪数据的预测，预测值与实际值的相关值分别为92.09%和91.23%。由以上分析可知，不含噪模型对噪声具有很好的容忍性。但是当随机森林模型的输入数据受到噪声污染时，预测过程中即使经过了去噪处理，预测结果依然包含大量的噪声。

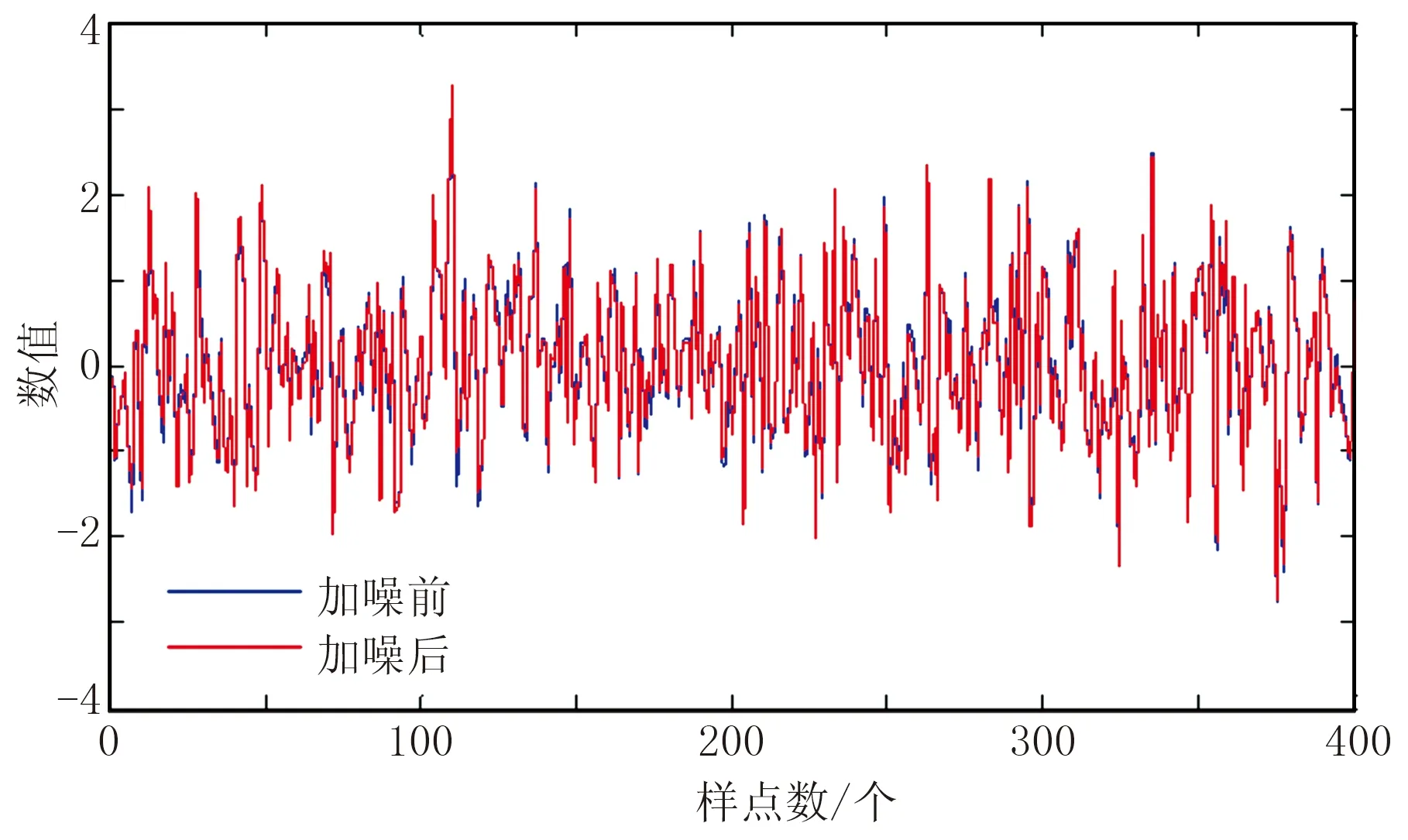
图1 变量加噪前、后对比图

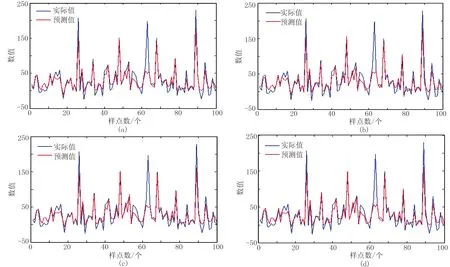
图2 实际值与预测值对比图

3.2 实际数据试验

采用公开的国外海上F3工区实际数据研究随机森林在处理回归问题中的容噪性，以预测结果能否有效刻画储层的地质特征作为评价标准。

F3是北海位于荷兰部分的一个区块，数据体上部1200ms内的反射层属于中新统、上新统和更新统。地震剖面上有一个非常明显的大型S型反射，是一个大型河控三角洲体系沉积体。工区内储层孔隙度总体很高(0.20～0.30)，从地震剖面上可以看到典型的下超、顶超、上超和削截构造现象，生物成因气藏引起的亮点反射也清晰可见[24]。工区所有井中的孔隙度数据均由密度计算得到

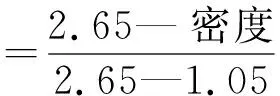
(2)

F3工区演示数据体的原始地震数据体包含相当大的噪声，适合于分析当输入数据受到噪声干扰情况下，随机森林对噪声的容忍度或稳健性。

3.2.1 地震数据滤波前、后信噪比分析比较

F3演示数据体除了提供原始地震数据之外，还有由Opendtect软件倾角控制模块进行中值滤波去噪处理的数据体，滤波去噪前后地震剖面如图3所示，可以看出经过滤波处理后，地震剖面上的同相轴更加清晰，更有利于解释构造特征。在随后的试验分析中以原始地震数据作为含噪声数据，滤波处理后的地震数据作为去噪数据。倾角中值滤波是对地震数据做平滑处理，消除了其中的相关性较低的噪声，信噪比得到提高，但分辨率有一定程度的降低[25，26]。

图4为两个数据体在层位(Demo6)切片上的平均信噪比，由SMI地震波形特征指示反演软件分析获得。图中浅蓝色曲线为SMI软件分析信噪比的一系列控制点，可见滤波处理后大部分区域地震数据信噪比得到明显提高，个别区域资料信噪比改善微弱。

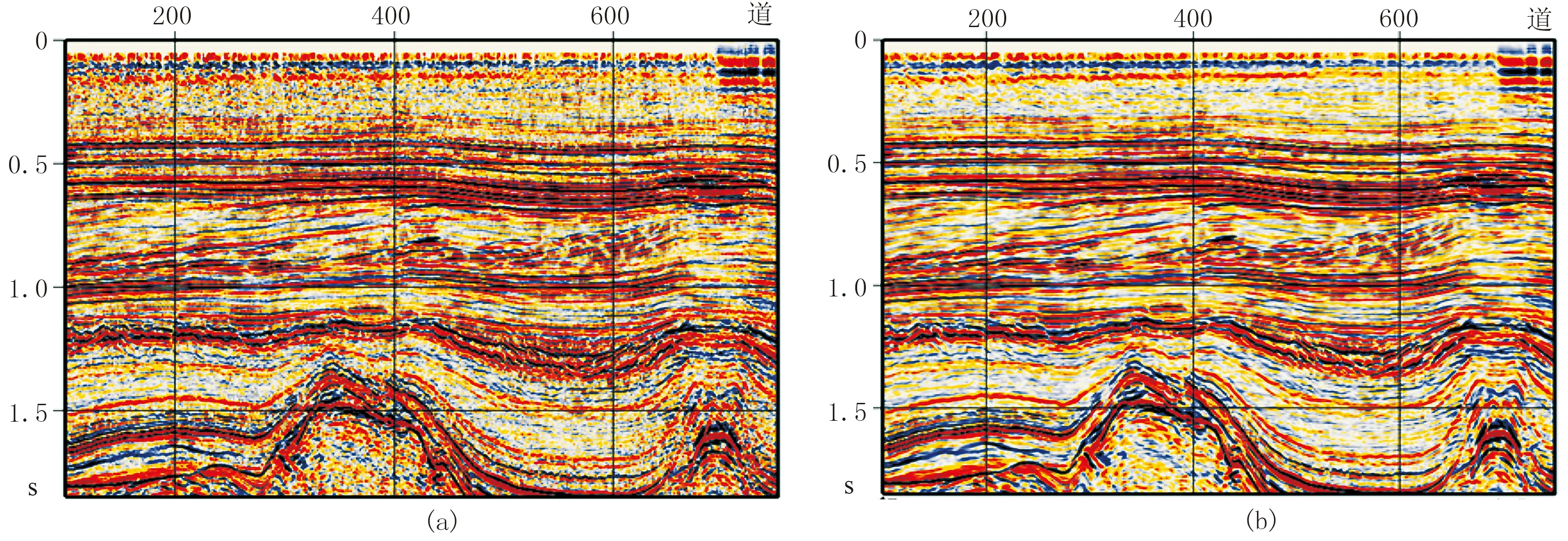
图3 去噪前(a)、后(b)地震剖面

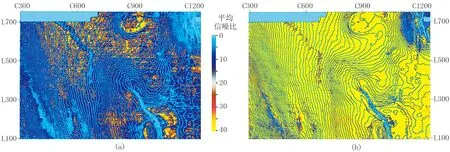
图4 去噪前(a)、后(b)地震数据信噪比分析结果

3.2.2 试验方法及结果分析

将随机森林回归方法应用于地震储层预测，提取F03-2井上的孔隙度数据作为预测的储层特征参数，并与对应的井旁道地震属性组成390个原始样本，孔隙度参数的极值为0.0568和0.3893，平均值为0.3192。地震数据中的亮点反射比较明显，提取的地震属性以振幅类为主，包括8种常见的地震属性：平均绝对值振幅、平均振幅、均方根振幅、弧长、平均能量以及“三瞬”属性。将孔隙度数据与含噪声的地震属性数据和去噪后的地震属性数据分别组成两个样本集——含噪声样本集与不含噪声样本集。

从两个样本集中随机提取3/4作为训练样本，用于构建随机森林模型，剩下的1/4作为测试样本检验泛化性能，决策树设置为500棵，随机特征选取个数设置为3，得到两个随机森林孔隙度预测模型，一个为含噪的随机森林模型，一个为不含噪的随机森林模型。将这两个模型应用于含噪数据(原始地震数据)和不含噪数据(中值滤波数据)，就得到四个孔隙度预测结果。从含噪数据(原始地震数据)和不含噪数据(中值滤波数据)对应的层位(Demon6)切片中分别截取同一位置进行显示(图4)，从孔隙度数据体中提取的层位(Demo6)切片如图5所示。

图6展示的是由含噪声样本建立的RF模型，分别使用滤波前、后的地震数据所提取的地震属性为输入，估算得到的两个孔隙度数据。图7是不含噪RF模型应用于滤波前、后的地震数据所提取的地震属性，估算得到的两个孔隙度数据体。

比较预测结果可知，这四个预测结果在横向上所展示的孔隙度分布特点大致相似，均能有效地刻画在该层位上发育的南北向分布的河道特征[27，28]，同时孔隙度数值主要为0.25～0.35，与实际的孔隙度(主要为0.20～0.30)情况是符合的。结合图4中的信噪比，可以看出在信噪比相对较高的区域，四个预测结果所刻画的储层特征是基本相同的，但在信噪比较低的区域，预测结果所反映的地质信息存在较大差异，由图6和图7可知导致出现差异的原因为所使用的模型样本数据是否含有噪声，表明样本的模型训练过程中输入数据是否含有噪声对预测结果影响较大，而在估算数据体的过程中地震属性数据中是否含有噪声对预测结果的干扰程度较小。

从地震剖面上分析，如图8和图9所示，可以看出RF模型的样本数据是否含有噪声对预测结果影响较大，图中黑色线为层位Demo6，该层位处于前积反射、超覆构造的上部。比较图8与图9的预测结果可知，当地震属性样本数据不含有噪声时，预测结果更加符合实际情况，对F3工区的超覆现象刻画效果更好，去噪模型的预测结果(图9)分辨率有所降低，其原因在于所使用的滤波去噪方法为倾角中值滤波，提高信噪比的同时付出了降低分辨率的代价。

试验结果表明输入数据在随机森林建模中起很重要的作用，训练样本的输入数据受到噪声污染时，输出结果受到噪声的影响较大，而在模型建立之后，估算数据体时地震属性数据是否做了去噪处理对预测结果的影响较小，可知当对样本的输入数据做了滤波处理，即在建立的模型受到噪声污染较少情况下，能表现出很好的容噪性。

图5 去噪前(a)、后(b)地震数据层位切片

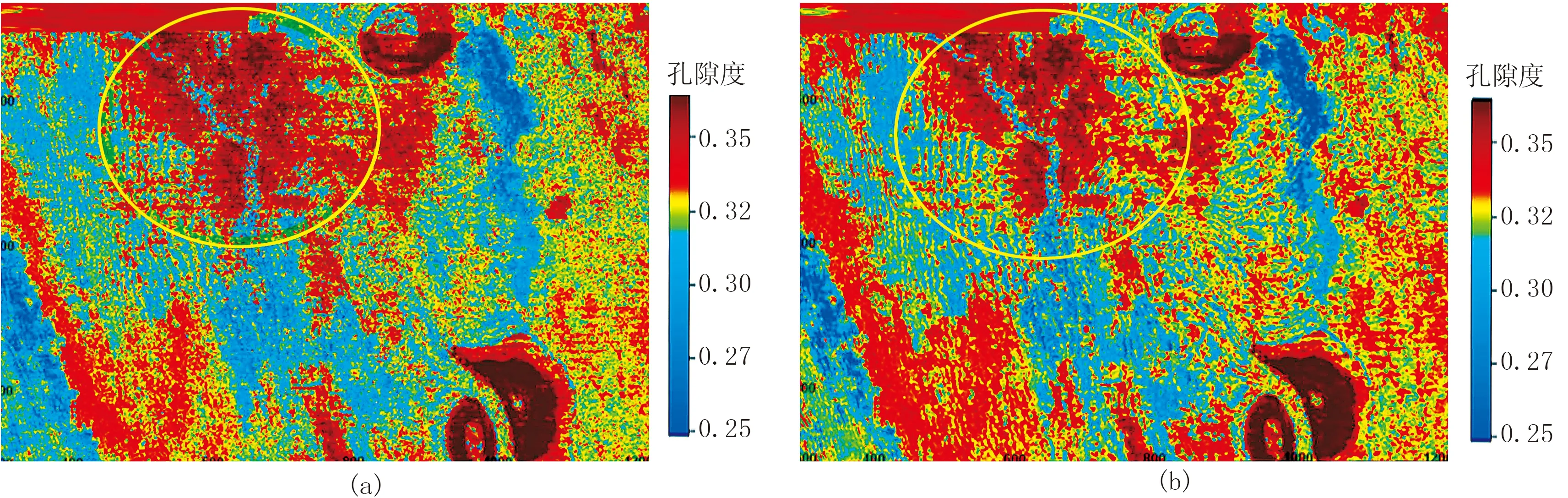
图6 含噪模型对地震数据滤波前(a)、后(b)预测的孔隙度层位切片

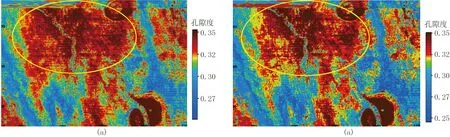
图7 不含噪模型对地震数据滤波前(a)、后(b)预测的孔隙度层位切片

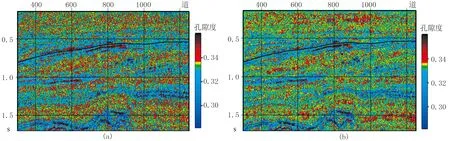
图8 含噪模型对地震数据滤波前(a)、后(b)预测的孔隙度剖面

4 讨论与认识

通过F3工区实际数据的容噪性试验分析，表明当训练样本的输入数据不含噪时，随机森林回归算法具有很强的容噪性，在预测过程中随机森林模型受噪声干扰较小。当训练样本的输入数据受噪声污染时，即使在预测过程中进行去噪处理，地震储层预测结果依然可能包含大量噪声。容噪性试验结果同时证明了随机森林算法具有较强稳健性，用于构建随机森林模型的样本数据在储层预测中占据很重要地位；在模型建立之后进行预测时，随机森林模型对异于样本信息的数据具有较强的容忍度。因此采用随机森林算法进行地震储层预测时，关键是提取不含噪声的样本数据。