交错网格有限差分正演模拟的联合吸收边界
2018-09-20胡建林宋维琪张建坤邢文军徐文会
胡建林 宋维琪 张建坤 邢文军 徐文会
(①中国石油大学(华东)地球科学与技术学院,山东青岛 266555; ②中国石油冀东油田公司勘探开发研究院,河北唐山 063004)
1 引言
复杂地下介质中,地震波的传播过程繁冗,难以得到解析解,因此,一般是通过正演模拟探究地下地震波的传播。在地震波正演模拟中,利用波动方程的正演模拟比用运动学的射线追踪法可获得更丰富的动力学信息,因此地震波场的数值模拟是地震波场传播研究中的重要手段之一[1-8]。
对声波方程进行网格离散时,采用交错网格的差分格式,可较好地压制数值频散,得到更高精度的正演模拟结果[2]。交错网格是指把速度及压力P分别定义于两套不同网格上的网格系统,该方法能更好地处理一阶波动方程中速度和压力的耦合关系。
在数值模拟时,边界问题就是找到一种合适的边界条件,使人为产生的计算区域边界在实际效果上是透明的,即不产生边界反射[3]。吸收边界条件正是一种产生反射非常小甚至不产生反射的人工边界条件。Smith[9]将Dirichlet边界条件与Neumann边界条件结合起来,由于两种边界条件产生的反射符号相反,两者相加抵消反射,但其计算量较大; Cerjan等[10]、Burns[11]提出基于扩大计算区域的吸收边界条件,该方法在扩大后的边界区使用阻尼机制减少反射波,以较大的计算量换取边界的吸收; Kosloff等[12]提出黏性阻尼方法以减少边界反射,但需进行波数域的变换。Clayton等[13]在网格边界附近用单向波动方程模拟声波和弹性波的传播,该方法对于入射角小于45°的入射波很有效; Liao等[14]提出边界外推方法,用来处理声波和弹性波的边界吸收问题; 基于频率域内声波和弹性波的吸收边界条件,Randall[15]提出分别处理胀缩波和旋转波分量的方法。Keys[16]和Higdon[17]在Clayton等[13]研究的基础上提出一种改进的吸收边界条件,成功消除了任意角入射波的边界反射,并具有良好稳定性。Bécache等[18]研究了时间和空间上的m阶Higdon边界体条件,发现当阶数m较大时,Higdon边界将变得异常复杂。
Berenger[19]在使用时域有限差分法时,为截断二维网格空间,提出PML吸收边界概念; Chew等[20]将PML引入弹性波模拟,采用扩展坐标系的PML方法; Rodent等[21]进一步提出CPML(convolutional complex frequency-shifted PML)边界条件,该边界在非线性、各向异性介质时效果更好; Gedney等[22]提出ADE-PML(the PML with Auxiliary Differential Equations)边界条件,该方法可将差分扩展到更高时间阶数; Liu等[23,24]提出一种混合吸收边界,采用一种过渡带方式从内部区域逐渐过渡到边界,进一步削弱了边界反射; Gao等[25]回顾了大部分典型的声波方程边界条件,并通过数值实验对比了各种方法。
至于将PML边界与Higdon边界的联合使用,尚未找到相关文献。本文将PML边界与Higdon边界构成联合吸收边界同时使用,比单独使用PML边界减小了边界厚度,也比单独使用Higdon边界具有更好的吸收效果。
2 三维声波方程交错网格有限差分正演模拟
交错网格有限差分法与常规网格有限差分法相比,计算效率更高,且能进一步提高数值模拟的运算精度,有效压制数值频散。三维声波方程交错网格有限差分正演模拟主要由传播方程、震源、边界条件三部分组成。
2.1 传播方程
在交错网格有限差分正演中,使用一阶压力—速度方程。在非均匀各向同性介质中,三维声波方程中的一阶压力—速度方程为
(1)
(2)
式中:P为压力;vx、vy、vz代表x、y、z方向的速度分量;V为纵波速度(声波速度);ρ为介质密度。
将式(1)、式(2)有限差分离散,即可得到一阶声波方程的时域迭代计算。
2.2 震源
震源子波函数有雷克子波、高斯子波、正弦衰减子波等。本文选用雷克子波
f(t)=A[1-2(πf0t)2]exp[-(πf0t)2]
(3)
式中f0为子波主频。
加入震源后,在震源处,式(1)变为
(4)
式中f(t)为震源子波函数,其他参数同式(1)。
2.3 边界条件
在数值模拟中,只能在有限的区域范围内进行模拟,如果不加任何处理,即在边界处压力值和速度值默认设置为0,那么地震波到达人工边界处时,将会产生非常强的反射,严重干扰内部波场。为了减少人工边界产生的反射波,需要再添加吸收边界。
人工吸收边界主要有两种吸收方式:匹配吸收边界条件(最外层单层匹配吸收)和衰减吸收边界层(有一定厚度的多层衰减)。文中联合吸收边界中的Higdon边界属于前者,而PML吸收边界则是后者。这两种边界的具体讨论见下文。
除了上面的三个交错网格有限差分的重要组成部分,有限差分离散时还需对离散格式的稳定性和频散进行分析。由于这部分并不是本文讨论的重点,所以略过。
3 PML吸收边界
PML吸收边界通过在垂直边界方向引入阻尼因子,选取适当的阻尼参数,使向边界外传播的波在匹配层中不断衰减,从而使反射波最大程度上得到削弱,实现消除边界反射的目的。该方法对一阶压力—速度方程时间域进行分裂,得到含有吸收衰减因子的吸收边界方程组
(5)
P=Px+Py+Pz
(6)
(7)
式中:dx、dy、dz分别为x、y、z方向的衰减因子,计算如下[26]
(8)
(9)
式中:L为PML边界总厚度,lx、ly、lz为PML边界内的点到最外层点的距离;d0为吸收系数的初始值;R=1.0×10-6为理论反射系数[27];β为控制PML吸收边界的吸收效果参数,常常设置为匹配层内的最大纵波速度。
PML吸收边界为有一定厚度的多层边界衰减,以沿-x轴方向传播的vx和Px分量为例,吸收边界的模式如图1所示。
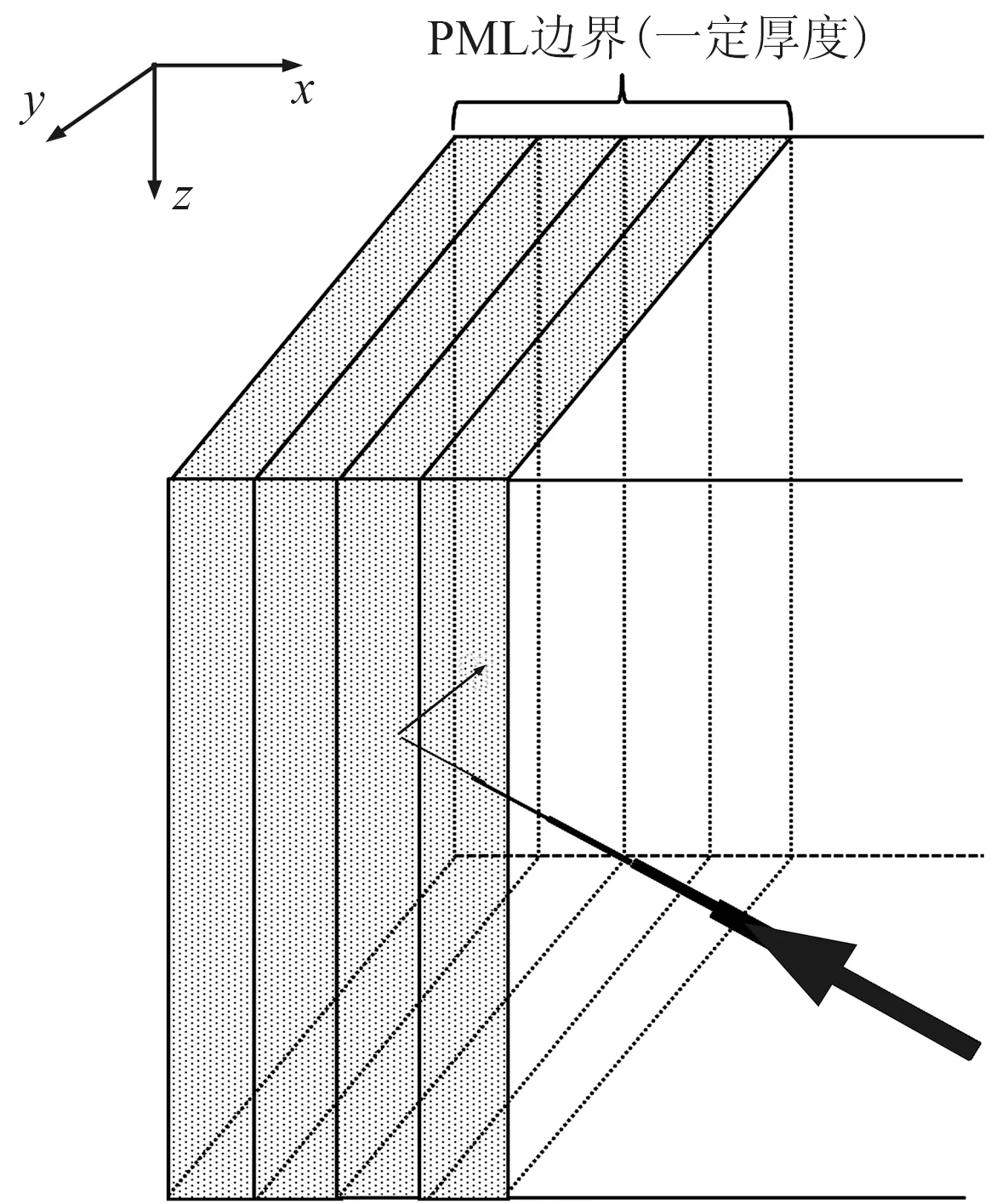
图1 PML边界层沿-x轴方向传播的vx和Px分量吸收示意图线的粗细代表能量大小
由图1可见,要使PML吸收层达到很好的吸收效果,可将PML层加厚。这种简单增加层厚度就能实现好的吸收效果是PML边界的优点,同时也会出现计算量问题。由于厚度的增加,使三维模型明显胖了一圈,导致计算量更为庞大。
4 Higdon吸收边界条件
Higdon[17,28]提出了具有下面形式的吸收边界条件(以x轴方向上的边界为例)
(10)
式中:m为吸收边界条件的阶数;c是入射波传播速度;αj是吸收入射角,第j个算子能完全吸收入射角为±αj的波。式中的反射系数为
(11)
式中θ为入射角。
m=1时,为一阶Higdon吸收边界,式(11)变为
(12)
m=2时,为二阶Higdon吸收边界,就有
(13)
在差分网格上离散后,吸收边界差分算子为
(14)
式中: 系数βj=cosαj,为正数; Δt、Δx分别为时间步长和空间步长;I为单位算子,满足
(15)
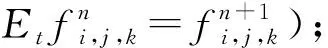
Higdon吸收边界为最外层边界匹配吸收,以沿-x轴方向传播的vx和Px分量为例,吸收边界的模式如图2。
Higdon边界仅有单层厚度,不会明显增加计算量,且能消除任意角度入射波的边界反射,具有良好的稳定性。但要想得到更好的吸收效果,必须使用高阶的Higdon吸收边界形式(m>2),而高阶时离散化后过于复杂,这是Higdon边界的一大缺陷。

图2 Higdon边界沿-x轴方向传播的vx和Px分量吸收示意图
5 联合吸收边界
5.1 联合吸收边界方法
由上文可知,PML吸收效果是通过一定厚度边界中的垂直分量衰减来吸收向边界外传播的波,而Higdon边界是根据偏微分算子消除一定角度的入射波。根据PML吸收边界和Higdon边界的吸收原理,结合两种吸收边界的优劣,研究了新的联合吸收边界,使向边界传播的波先经过PML边界进行衰减,然后到达最外层Higdon边界时,再对残余的波进行匹配吸收,最大限度地削弱边界反射。以x轴方向的左边垂直分量的边界为例,吸收边界的模式如图3所示。
图3 联合吸收边界上沿-x轴方向传播的vx和Px分量吸收示意图线的粗细代表能量大小
由于在PML层最外层联合使用了Higdon吸收边界,因此在相同吸收效果下,可减小PML层厚度,从而减少计算量。
5.2 联合吸收边界方程推导
针对研究的联合吸收边界方法,对新的吸收边界方程进行推导。为了最大程度简化推导,先考虑在PML吸收边界内沿x轴方向传播的平面波,此时PML边界内的一阶声波方程(式(5)~式(7))简化为
(16)
设vx0、Px0分别为分量vx、Px的幅值,则PML介质中传播的波场可表示为[29]
(17)
将式(17)代入式(16),可解得
(18)
将式(18)代入式(17)可得PML介质中传播的波场
(19)
将式(19)写为更一般的平面波形式,可得PML边界中沿着坐标轴传播的平面波方程,以速度V沿x轴向x>0空间运动的平面波表示为
(20)
由上式可推导得到x=0边界上的Higdon形式的吸收边界条件算子
(21)
将上面的算子应用于沿x轴传播的平面波时,反射波场的值该为零。因此在x=0边界上,PML吸收层内,m阶的Higdon形式的吸收边界条件可写为
(22)
同理,可对波场区域的其他边界上的PML层内的Higdon形式吸收边界进行类似的推导,得到对应的Higdon边界条件。
5.3 联合吸收边界算法及其计算步骤
将推导得到的联合吸收边界方程,加入到有限差分离散方程中,通过差分算法的研究,形成了联合吸收边界的交错网格有限差分算法,算法的波场更新计算如下:
一、根据三维声波方程中的一阶压力—速度方程(式(5))对边界内部与x,y,z有关的压力分量单独进行波场更新;
二、对PML边界内的压力分量采用含衰减因子的PML吸收边界方程组(式(5)、式(8))进行边界内压力分量波场衰减更新;
三、对最外层Higdon边界进行压力分量波场更新;
四、使用P=Px+Py+Pz(式(6))对各方向的压力分量进行求和;
五、根据三维声波方程中的一阶压力—速度方程(式(7))对边界内部与x,y,z有关的速度分量单独进行波场更新;
六、对PML边界内的压力分量采用含衰减因子的PML吸收边界方程组(式(7)、式(8))进行边界内速度分量波场衰减更新;
七、对最外层的Higdon边界采用Higdon边界吸收算子(式(22))进行速度分量波场更新;
根据上述的波场更新步骤,反复进行迭代,即可得到边界吸收良好的联合吸收边界正演模拟。
6 数值分析
设计均匀各向同性的层状介质模型,介质层数为7层,模型尺寸为500m×600m×700m,模型网格尺寸为5m×5m×5m,网格数为Nx×Ny×Nz=101×121×141。震源使用40Hz的雷克子波,设置位置为(250m,300m,0m),接收线过震源,且与y方向平行,同样间隔5m,共101个检波器。层状模型和炮检分布如图4,各层参数分布如表1所示。
使用高阶交错网格有限差分算法,对层状介质进行正演计算,当PML厚度足够时,能够较好地吸收边界的反射。当PML边界厚度为15个点,观察270ms时压力P的波场快照和480ms长度的炮集记录,可见有明显的边界反射(图5b、图6b);在PML边界外,再用一阶Higdon边界进行吸收,可见边界反射得到明显减弱(图5c、图6c);在PML边界外,再用二阶Higdon边界进行吸收,可见边界反射得到进一步减弱(图5d、图6d),此时吸收效果与30个点厚度的PML边界(图5a、图6a)相近。通过结合Higdon边界,弥补因边界厚度不足导致的吸收不足,体现出联合吸收边界的优越性。
从表2正演模拟耗时统计可发现,与单纯的PML边界相比,达到相同的吸收效果时,联合吸收边界大大减小了运算量,PML边界(15点厚度)联合二阶Higdon边界与PML边界(30点厚度)相比,同样吸收干净,但耗时约为后者的62%,大大减少了计算量。
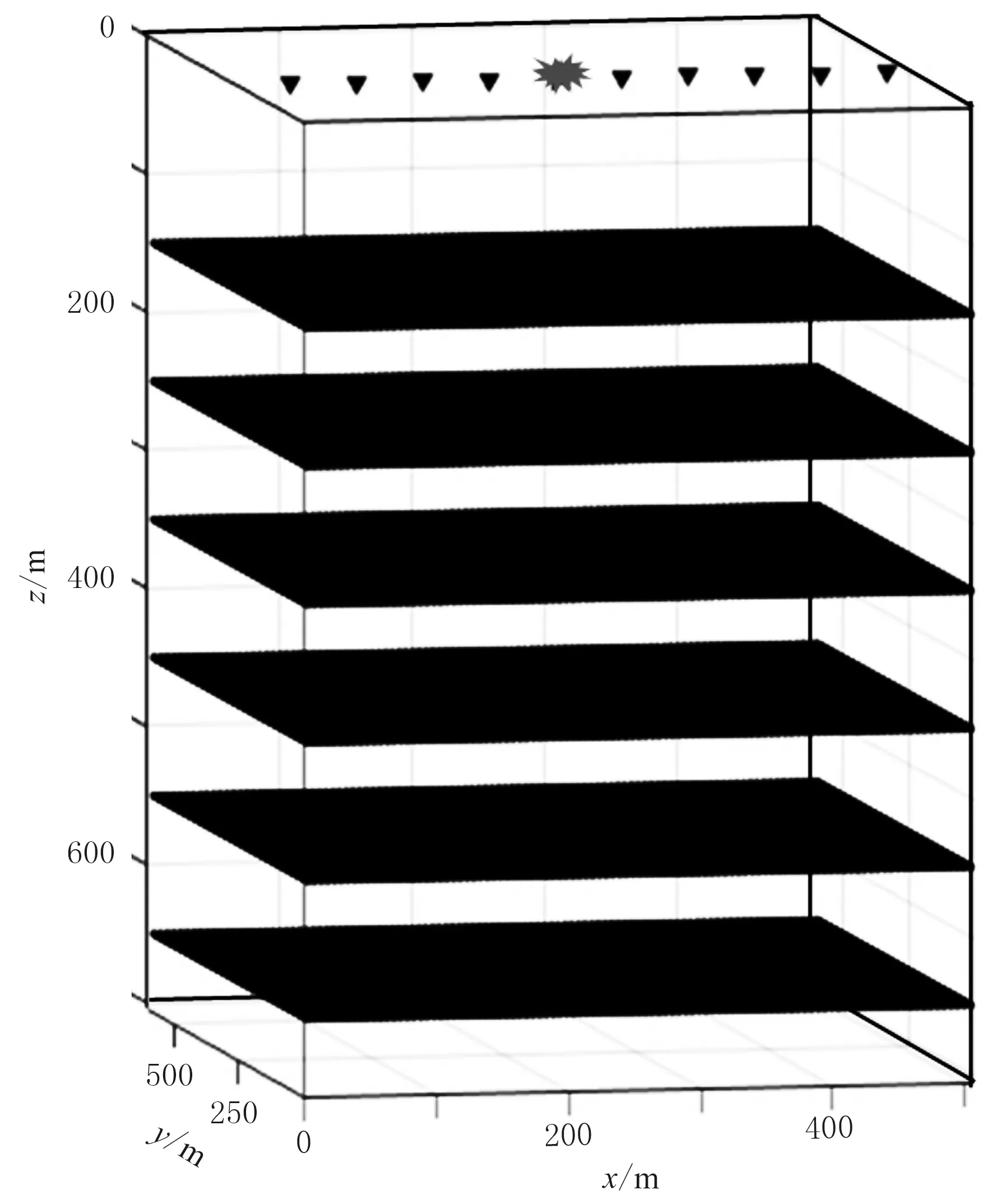
图4 层状模型和炮检分布示意图
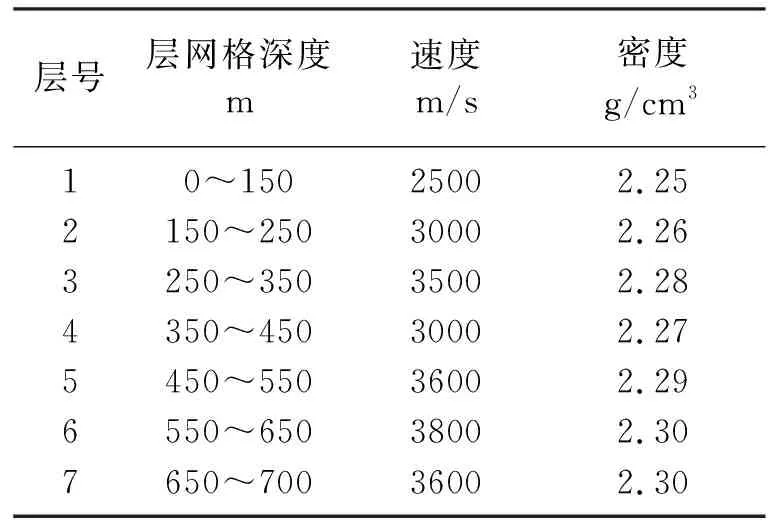
层号层网格深度m速度m/s密度g/cm310~15025002.252150~25030002.263250~35035002.284350~45030002.275450~55036002.296550~65038002.307650~70036002.30

图5 270ms时接收线剖面上P分量波场快照
(a)PML边界(30个点边界厚度); (b)PML边界(15个点边界厚度); (c)PML边界(15个点边界厚度)+一阶Higdon边界; (d)PML边界(15个点边界厚度)+二阶Higdon边界
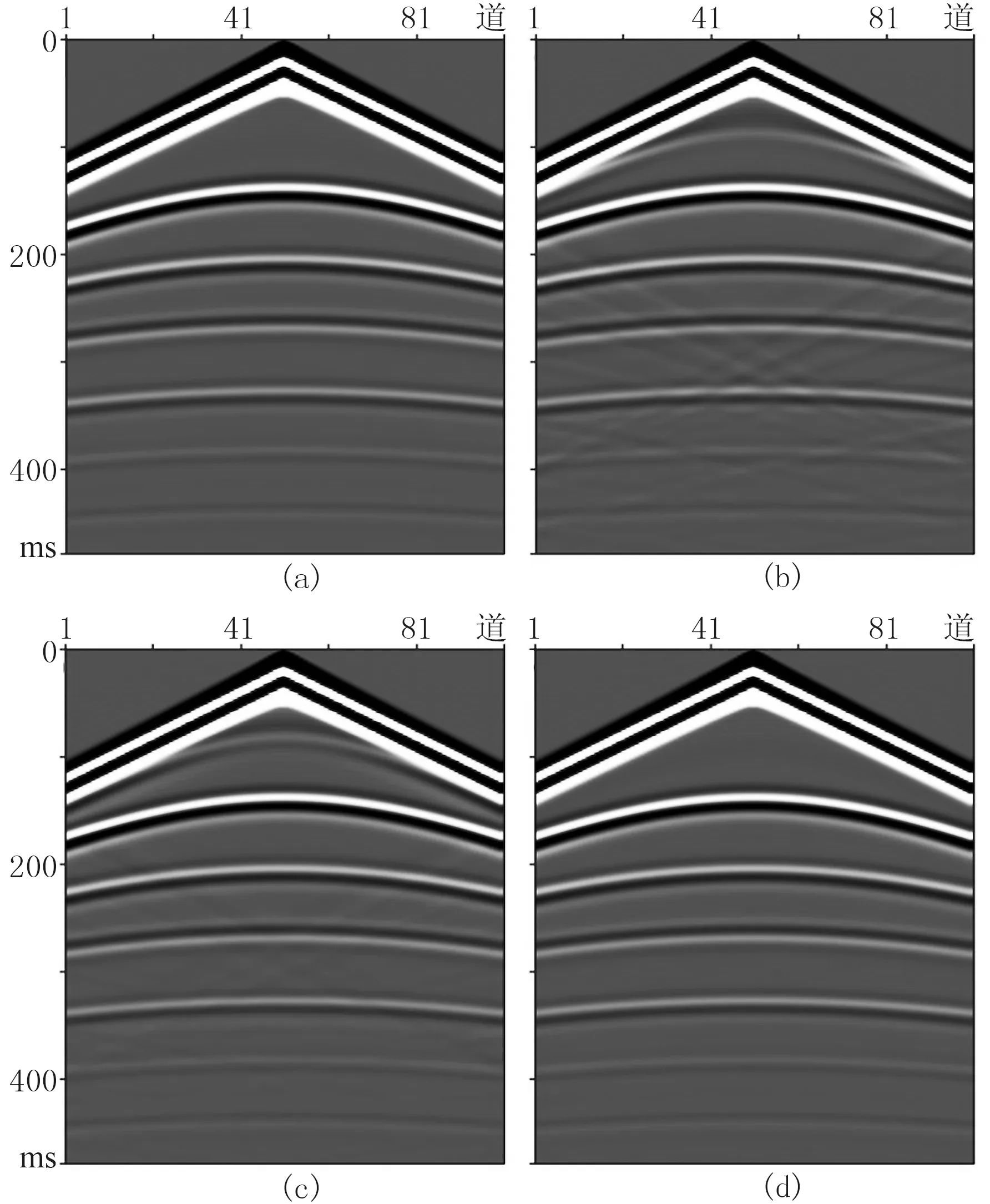
图6 P分量炮集记录
(a)PML边界(30个点边界厚度); (b)PML边界(15个点边界厚度); (c)PML边界(15个点边界厚度)+一阶Higdon边界; (d)PML边界(15个点边界厚度)+二阶Higdon边界
7 结论
本文将PML边界与Higdon边界结合起来,得到联合吸收边界,对各向同性多层介质的声波波场模拟,并且通过对比分析,可发现联合吸收边界具有如下优势:
(1)联合吸收边界相比单纯的PML吸收边界,可使用较小的PML边界厚度,使模型大小明显减小,较明显地减少了计算量;
(2)与Higdon边界相比,联合吸收边界结合了PML的吸收特性,能够更有效地吸收边界反射,获得更好的模拟结果。
