基于特征选择和神经网络的铁路货运量预测

（华中科技大学 土木工程与力学学院，湖北 武汉 430074）

1 引言

铁路货运量是确定铁路基础设施建设规模、安排货物运输计划的重要依据，是铁路货运市场体系的重要指标。货运量预测的准确性对制定未来铁路货运发展战略、货运设施的投资和效益都有着重要的意义。铁路货运部门一直力图及时、准确地对铁路货运量进行预测和分析。铁路货运体系是一个复杂系统，受社会、经济、自然等多种因素的综合影响，铁路货运量是一个非线性时间序列，这就导致了建立预测模型十分困难。

就整个交通预测问题而言，已经有了大量研究成果。大体可以把它们分为两类[1-2]：一类是动力模型，包括时间序列模型、卡尔曼滤波模型、参数回归模型、指数平滑模型等；另一类是统计模型，包括非参数回归模型、KARIMA算法、基于小波理论的方法、基于多维分形的方法、谱分析法、状态空间重构模型和神经网络模型等。前者试图在预测依据与预测对象之间建立明确的函数解析式关系，后者主要通过对数据的学习，发现预测依据与预测对象之间的多层嵌套的相关性，并不追求严格的数学形式和明确的物理意义，而更重视对预测对象的拟合效果。

无论采用何种预测模型，若仅仅依据被预测对象自身的时间序列数据进行预测，则预测精度达不到预期效果，毕竟单变量的时间序列提供的信息是有限的。考虑到多变量时间序列包含更丰富的预测对象所隶属的系统相关信息，能重构出更为准确的相空间，引入除预测对象以外的其他指标构成多维时间序列，可体现预测对象受多种因素共同驱动的本质[3-5]。

有一些学者已经将多维时间序列用于交通预测，例如用于交通事故预测[6]、驾驶状态检测[7]、交通流状态预测[8]以及短时交通流量预测[9]。其中，文献[6-8]采用的是分段线性回归的方法，与非线性预测仍有较大差异。文献[9]采用了相空间重构方法，在理论上较为先进，但基于贝叶斯的相点融合在应用上十分繁琐。

作为一种经典的统计学习模型，人工神经网络可以任意逼近复杂函数，因此，它在时间序列的学习和预测中具有天然的优势。正因如此，神经网络在交通预测领域得到广泛应用，例如，朱中[10]等人采用神经网络实时预测交叉口的交通流量；谭满春[11]等人将自回归求和滑动平均与人工神经网络组合模型用于短时交通流预测。这些研究属于早期研究，受数据来源的限制，神经网络所处理的是单个时间序列而不是多维时间序列。利用神经网络对多维时间序列进行学习和预测可较为轻松地取得较好的效果[12]。一方面，神经网络具有强大的特征提取与抽象能力，能够整合多维信息，处理异构数据，捕捉变化动态，是分析多维数据的有力工具；另一方面，多维数据也可为神经网络提供充足的训练样本。但是，如何明确神经网络的结构和大小，以及如何克服数据中的矛盾和错误对神经网络训练和学习造成的干扰仍然未得到解决。

本文将基于神经网络的时间序列预测分为两个阶段。第一阶段，对输入神经网络的指标项进行特征选择。首先，对指标项进行筛选，降低时间序列的维数，只保留与铁路货运量具有较强相关性的那些指标。然后，对所保留的指标项进行模糊聚类，以增强那些与除铁路货运量之外的其他指标高度相关的指标在神经网络训练和预测中的作用。第二阶段，建立基于广义回归神经网络（GRNN）的预测模型。经由广州市的年报统计数据验证，将特征选择与基于GRNN的预测模型相结合，会大大提高预测精度。

2 特征选择

2.1 指标筛选

神经网络建模所需的信息完全由训练样本提供，这就决定了建模效果的好坏依赖于训练样本的数量和质量[13]。通常情况下多维时间序列具有较多特征指标，由于特征空间维数较大，使得多维时间序列预测存在“维数灾难”的问题。因此选取对预测具有一定作用的特征指标是预测的前提和难点。特征选择是指从原始特征集中选择使某种评估标准最优的特征子集，是一种常见的降维方法，其目的是使选出的最优特征子集所构建的分类或回归模型达到和特征选择前近似甚至更好的预测精度。

本文首先对各项指标进行筛选，只保留与铁路货运量的线性相关性≥0.7的指标。大量经验表明，相关性在0.7以上即是具有较强的相关性[14]。相关性的计算公式：

式中：r—相关性系数；y—铁路货运量；—铁路货运量均值；x—需要计算的指标；—需要计算指标的均值。

2.2 指标的模糊聚类

2.2.1 模糊聚类方法。大多数事物的属性并不是完全确定的，它们在性态和类属方面存在着亦此亦彼的模糊性。模糊聚类允许对元素的分类存在交叉性，即允许一个元素同时出现在多个类中。对指标进行模糊聚类，本质上是允许指标的相似性和差异性同时存在，以抵消指标之间的矛盾给训练神经网络带来的干扰。多维时间序列中的矛盾很多，对指标进行聚类显得尤为必要。

对隶属度的计算方法有很多种，本文假定各指标之间的相关性就是隶属度，相关系数越接近1则隶属度越强。隶属度（相关性）可作为对集合中的元素进行分类的标准[15]。设指标集合X={x1,x2,x3,x4,x5}，根据X中各元素的相关性给出模糊相似关系R，由于模糊相似关系满足自反性与对称性，所以其对应的矩阵主对角线上全部为1，且具有对称性。模糊相似矩阵如图1所示。取截集水平λ=0.7，令图1矩阵中大于等于λ的值变为1，小于λ的值变为0，如图2所示。根据图2中的矩阵所反映的相关关系，可将X中的元素分为{x1,x2}、{x1,x4}、{x2,x3}、{x2,x5}四类。

图1 模糊相似矩阵

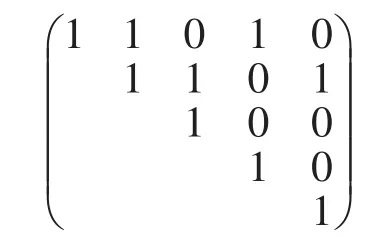
图2 截集矩阵

2.2.2 模糊聚类步骤。与铁路货运量相关的若干个指标之间并不一定两两相关，所以把类中各指标必须两两相关作为分类的标准，以保证类中的指标较为紧凑。在进行模糊聚类时，搜索起点采用随机选取，搜索方向使用前向搜索，即初始集合为空集S，随机选取初始指标后按照一定的搜索顺序从未包含在S的指标集中按照一定规则选取新的指标加入S构成一个类。搜索策略采用随机搜索，即选择特征的顺序为随机顺序。停止准则是当所有特征都进行分类后则结束模糊聚类。聚类过程如下：

（1）从全部指标项中随机选取一项作为初始类的第一个元素。

（2）把剩下的指标按照随机顺序依次与已有类中的每一个指标比较相关系数，若相关系数都≥λ则将该指标添加进这个类中，若不满足则不对该指标进行分类。

（3）检查是否所有指标都进行了分类，若是，则结束聚类；若否，则分别计算所有未分类指标与已分类指标的距离，即相关系数之和。选取距离最远的未分类指标作为新类的第一个元素并且返回第（2）步。

由于聚类时挑选指标的顺序存在随机性，因此每次聚类结果不完全相同，但经过多次分类发现，每次分类的数量和类中的指标数量均较为稳定。

3 基于GRNN的时间序列预测模型

3.1 GRNN模型

鉴于政府统计部门所提供的年报数据含特征项数量较多而年份项数量较少，本文选用具有学习速率快、人为确定参数少特点的广义回归神经网络（GRNN）建立学习和预测模型。GRNN收敛于样本量积聚较多的优化回归面，并且在样本数据较少时，预测效果也较好。而另一种常见的神经网络—BP神经网络，在训练时存在收敛速度慢和容易陷入局部极小的缺点。

广义回归神经网络（GRNN）由四层构成，分别为输入层、模式层、求和层和输出层。当一个神经网络模型“学习”得到输入和输出变量的关系之后,即可用于对给定输入的预测。一个预测样本个数为N、预测样本输入量维数为M、预测样本输出量维数为K的GRNN结构如图3所示。

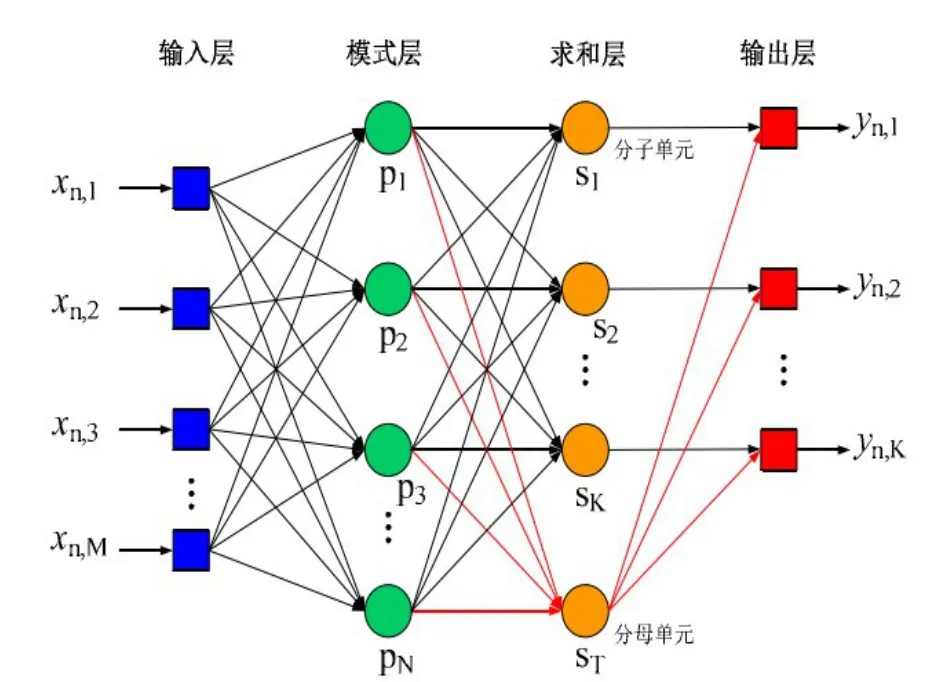
图3 广义回归神经网络结构图

（1）输入层。输入层接收样本的输入，即预测年份的除铁路货运量以外的其他各项指标，将它们归一化后通过线性函数直接传递给模式层。

（2）模式层。模式层中的神经元为径向基神经元，其个数与训练样本数相同。模式层的本质是利用径向基函数计算预测样本与训练向量之间的相似程度。它接受输入层的输出向量xn=[xn,1,xn,2…xn,M]T，然后计算输入向量xn与该层训练向量的欧氏距离‖dist‖，训练向量为cj=[cj,1,cj,2…cj,M]T（其中j表示第j个神经元）。

式中：xn-第n个输入样本；cj-第j个径向基神经元训练向量。

最后，以输入向量和训练向量之间的距离‖‖dist作为自变量传递给该神经元的激活函数。径向基神经元的激活函数采用径向基函数，通常定义为空间任一点到某一中心之间的欧氏距离的单调函数，一般表达式为：

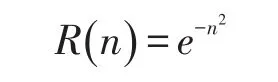
径向基神经元中常用的径向基函数是高斯函数，因此径向基神经元的激活函数可表示为：

式中：xn-第n个输入样本；cj-第j个径向基神经元训练向量；σ-高斯函数的方差，即光滑因子。

则第n个输入样本的第j个神经元的输出值即Pn,j=R(xn-cj)。其中σ由人为确定。

（3）求和层。求和层包括两种类型神经元，其中一类为分母单元，另一类为分子单元。分母单元是对模式层的输出进行算术求和，模式层各神经元与分母单元神经元的连接权值为1，其输出为：

式中：Pnj-第n个输入样本的第j个神经元的输出值。

分子单元是对所有模式层神经元的输出进行加权求和，求和神经元的个数为预测样本输出向量的维数K，在本例中需要预测的只有铁路货运量即K=1。分子单元与模式层神经元的连接权重为训练向量中当年的铁路货运量yj，即wj,k=yj。分子求和神经元的输出为：

式中：Pn,j-第n个输入样本的第j个神经元的输出值；wj,k-第k个分子单元与第j个模式层神经元的连接权重。

（4）输出层。所谓输出就是预测结果。输出层中的神经元个数等于预测样本中输出向量的维数K，这里只有铁路货运量需要预测，所以K=1。神经元将求和层的分子单元输出除以分母单元输出，得输出层神经元的铁路货运量输出为：

式中：yn-第n个预测样本的铁路货运量预测值；Sn-第n个预测样本的分子单元输出；STn-第n个预测样本的分母单元输出。

从广义回归神经网络的结构可以看出，其实质就是能够实现不同模式下的局部响应，从而达到全局逼近的训练效果。因此广义回归神经网络可进行模式识别下的预测。

3.2 模糊聚类对于GRNN的作用

需要指出，对指标进行模糊聚类与构建模糊神经网络是两种不同的技术方法。前者将具有较高相关性的指标归为一类，旨在梳理数据空间本身的结构。后者将模糊规则引入神经网络，使网络的训练过程具有模糊性。由于GRNN的实质是度量某个样本与其他样本之间的相似性，而样本之间的相似性本来就不互相排斥，所以，GRNN等价于模糊神经网络，没有必要再通过模糊化来提高对训练样本的兼容性。

虽然GRNN具有等价于模糊神经网络的功能，但样本内部数据本身的矛盾，仍会影响GRNN的效果。相互矛盾的数据将对计算样本之间的距离造成影响，而神经网络的模糊化不能解决数据样本本身的矛盾，可以通过对训练样本进行模糊聚类来解决这个问题。

聚类使导致矛盾的异常数据落入少数几个类甚至是1个类中，降低了它们在训练中出现的次数和影响，同时增加关联性较强的数据出现的次数和影响。神经网络的优势是经验风险最小化[14]，聚类的本质是降低数据带来的结构风险，恰好弥补了神经网络固有的不足。

4 预测案例

4.1 数据预处理

广州市1999至2015年的宏观年报共统计了人口、产业、物价指数、投资、消费、运输与邮电等方面的1 294项指标，为避免其中部分指标在部分年份缺失对神经网络训练效果的影响，只选用了缺失年份少于等于2年的906个指标。再按与铁路货运量线性相关性≥0.7的标准，最后保留92项指标。将两两之间线性相关性≥0.7的指标归入一类，92项指标共被分为15个不同的类，每一类的元素个数从几个到几十个不等。为了描述方便，将1号指标设置为铁路货运量。

数据在输入神经网络前需要被归一化处理，这里使用最大-最小标准化公式对每一数据项的时间序列进行归一化处理：

式中：A-需要归一化的指标；x-指标中的年份数据；x'-指标中归一化后的年份数据。

在进行归一化处理后，以广州市1999-2009年11年间的数据作为11个训练样本，并以当年铁路货运量为目标，以2010-2015年6年间的数据作为预测样本，预测相应年份的铁路货运量并计算误差。

4.2 预测结果

为说明特征选择的作用，分别将进行指标筛选和模糊聚类、进行指标筛选但不模糊聚类、未进行指标筛选但模糊聚类、未进行指标筛选和未模糊聚类四种不同的特征选择方案的结果输入GRNN网络进行预测，预测结果如图4所示，四种特征选择方案所对应的预测误差见表1。

表1 不同特征选择方案对应的预测误差

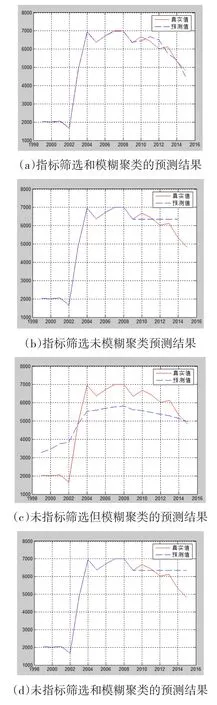
图4 铁路货运量预测结果

当特征选择手段既包括指标筛选又包括模糊聚类时，根据指标所分成的15个类共得到15个不同的预测结果，取平均值得到最后铁路货运量的预测结果。

当特征选择不进行模糊聚类分析，直接将筛选过后留下的92项线性相关指标带入神经网络进行训练时，神经网络没有给出有效的预测值。

当特征选择对指标不进行筛选但进行模糊聚类时，906项指标共被分为154个不同的类，每一类的元素个数从1个到几百个不等。由于此时数据样本数量较少，但类的个数很多，进行预测时，对所有类取同一光滑因子σ将产生问题。较小的σ导致神经网络拟合能力较好，但外推预测效果较差，较大的σ会使那些与铁路货运量之间存在简单对应关系的类所产生的预测结果的精度不够。因此，难以找到一个适合所有类的光滑因子σ。

当特征选择未对指标进行筛选和未模糊聚类时，直接将906项数据项带入神经网络进行预测。训练样本数量较少且维数较大，存在数据错误和数据矛盾，神经网络几乎没有预测效果。

由图4和表1可以看出，采用既数据项筛选又模糊聚类的特征选择方法能使神经网络对铁路货运量进行有效的预测。

5 结论

铁路货运量是铁路基础设施投资建设、安排货物运输计划的重要依据。本文首先简述了传统铁路货运量预测方法的不足以及多项指标构成多维时间序列对预测带来的数据融合问题。然后介绍了在将数据输入基于广义回归神经网络的预测模型之前，采用数据筛选和模糊聚类相结合的特征选择方法。指标筛选保证了指标与铁路货运量之间的相关性，指标聚类则增强了那些与其他指标高度相关的指标在神经网络训练和预测中的作用。

将广州市1999至2009年的1 294项年报指标进行筛选和模糊聚类后，保留其中92项，并将它们分为15类，然后输入广义回归神经网络预测模型，对2010至2015年的铁路货运量进行预测，误差在1.5%-8.2%之间。同时，本文从反面验证了不进行数据筛选或不模糊聚类的特征选择方法将使预测结果产生较大误差，说明进行指标筛选和模糊聚类的特征选择对于基于广义回归神经网络的预测模型是非常必要的。