基于数学核心素养的课堂重建——“三三三”学案教学法
2018-09-20海南省农垦中学肖世琥
□ 海南省农垦中学 肖世琥
史宁中教授在 “数学核心素养和小学数学教学”这个专题报告中指出:数学教学的关键是启发学生学会数学思考,帮助学生积累活动经验,使学生会用“数学的眼光观察世界”“数学的思维分析世界”和“数学的语言表达世界”,这是制定数学核心素养的依据。具体要素包括:数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六个维度。而“三三三”学案教学法,就是把“知识点”与“例题”,通过精心的设计,融入到三组系列问题中,再通过学生自主学习,合作学习,教师深入浅出的点拨,达到提升学生数学核心素养的良好效果。笔者反思整个教学实践历程,从以下三个维度来考虑和操作,是可以解决上述问题的具体做法:
一、“三三三”学案教学法的形成与解读
从1984年9月至1987年7月,笔者使用中国科学院心理研究所卢仲衡教授编写的《中学数学自学辅导教材》,按“启、读、练、知、结”五步进行教材与教法改革实验。1987年9月至2003年7月,将“启、读、练、知、结”五步教学法移植到统编教材,形成了具有个性化的“启、读、议、练、结”五步教学法。在2003年9月至今任教高中数学以来,自己一直致力于高中数学教学改革,尤其是近三年间在高一的数学教学实践中,基于落实数学核心素养的原则性要求,又将五步教学法发展为“三三三”学案教学法。
第一个“三”是:课堂教学有三个环节。第一个环节是“阅读思考”,第二个环节是“探究新课”,第三个环节是“巩固提升”。第二个“三”是:每个环节中,设计有梯度的三个问题,使之形成问题链。第三个“三”是:针对三类不同层次的学生提出不同的学习要求,即对于“阅读思考”中的三个问题,要求所有学生在课前要认真阅读教材,一般用15分钟左右完成;对于“探究新课”中的三个问题,要求中等以上的学生全体达标,而学习有困难的学生只需部分达标即可。对于“巩固提升”中的三个问题,要求成绩优秀学生达到目标,中等水平学生部分达标,其他学生不作要求。
关于学案中问题的设计,“阅读思考”是以围绕新知识点生长为主脉,一般有一个诊断性问题,它的作用是承前启后,既复习了旧知识,又激发学生阅读教材的动机和主动性。另外两个问题最好是学生通过阅读教材中部分段落后,从文本中就能找到,或者是教材练习中的相关问题,进而培养学生阅读数学课本的能力。在教学进程中,一般通过提问的方式落实“阅读思考”中的三个问题,教师从学生的回答当中积累素材,作适当的点拨和讲解。在设计“探究新课”中的三个问题时,尽量地将教材中的重、难点,设计成有层次的三个问题,通过师生共同探究,使学生掌握重、难点知识的形成和发展过程,明确注意点及解题方法。在设计“巩固提升”的三个问题时,既有检测本节课学生所学知识的相关性问题,也有综合前面所学知识的问题,或者适当有超越课本内容的创新性问题。有时对最后这个问题可让学生课后完成。在实施过程中,通过合作讨论,师生互动,就是“三三三”学案教学法的目的所在。
二、“三三三”学案教学法的实施案例分解
1.方程的根与函数的零点的学案。
(1)阅读思考。掌握函数零点的概念及没有区间限制的函数零点的存在问题。
【问题1】阅读教材P86至P88探究上面的内容,回答:
①方程x2-2x-3=0的根为 __________;
②函数y=x2-2x-3与x轴的交点坐标为_____;
③函数y=x2-2x-3的零点为__________。
归纳:“方程 f(x)=0 的根”“函数 y=f(x)图像与 x轴的交点”与“函数 y=f(x)的零点”可互相_______。
【问题 2】若函数 f(x)=x+a 的零点为 2,则函数 g(x)=x2-ax的零点为_______________。
【问题3】若函数y=x2-x+a存在零点,则实数a的取值范围为____________________ .
(2)探究新课。探究有区间限制的函数零点的存在问题。
【问题 4】观察函数 f(x)=x2-2x-3 的图像,从中可以发现函数在区间[-2,1]上有零点吗?其中满足f(-2)·f(1)_______________;
其中也满足 f(-2)·f(1)__________ ;
【问题 6】函数 f(x)=3x-x2在区间(-1,0)上有零点吗?你能说明理由吗?
归纳函数零点存在定理:若函数y=f(x)在区间[a,b] 上的图像是_______的一条曲线,且有_____,则函数 y=f(x)在区间(a,b)上有零点。(3)巩固提升。通过下列问题归纳函数零点的三种解题思路。
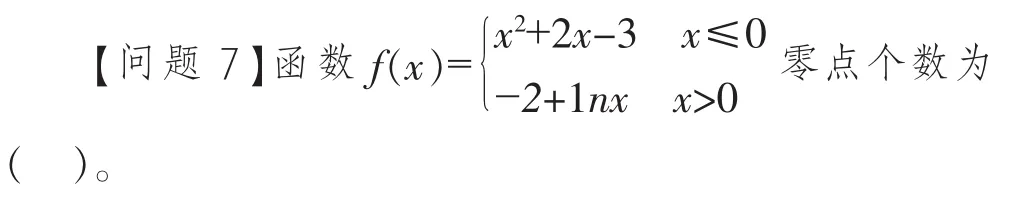
A 3 B 2 C 1 D 0
【问题 8】在下列区间中,函数 f(x)=1nx+2x-6 的零点所在区间是()。
A (0,1) B (1,2) C (2,3) D (3,4)
【问题 9】函数 f(x)=ex-x3的零点个数为( )。
A 0 B 1 C 2 D 3
2.“阅读思考”环节的教学实录。
逐一提问三位学生回答“阅读思考”中的三个问题。(注:学生1、2、3均为学困生)
学生 1:(1)3,-1;(2)(3,0),(-1,0);(3)3,-1.
教师:你从问题1中的三个小问题中发现了什么?
学生 1: “方程 f(x)=0 的根”“函数 y=f(x)图像与x轴的交点”与“函数 y=f(x)的零点”可互相转化。(教师同时板书)
教师:函数的零点就是对应方程的根。
学生 2:0,-2。
教师:怎么求的?
学生3:根据题意得,x=2是方程x+a=0的根,求得a=-2,代入得方程x2+2x=0,解方程求得结果。
教师:这个问题反复利用函数的零点就是对应方程的根来求解。
教师:如何思考的?
学生3:根据题意得,函数y=x2-x+a图像与a轴有公共点,利用根的判别式△=1-4a≥0可求得结果。
教师:这位同学是将“存在零点”转化成“图像与轴有公共点”,实际上,也可以转化成“对应的方程有实数根”来思考。这道具体问题的解答,可帮助学生理解教材 P87中,一元二次方程 ax2+bx+c=0(a≠0)的实数根与二次函数 y=ax2+bx+c=0(a≠0)与 x轴的交点,及函数零点问题的相互转化。
3.“探究新课”环节的教学实录。
逐一提问三位学生回答“教学新课”中的三个问题。(注:学生4、5、6均为中等生)
学生 4:有零点, f(-2)·f(1)=-20<0。
教师:你是如何看出有零点的?请同学们看教材P87探究中的内容。
学生 4: 函数 f (x)=x2-2x-3图像在区间[-2,1]上与x轴有交点。
教师:函数 f(x)=x2-2x-3 在区间[-2,1]上,满足端点的函数值互异,即在x轴上方有图像,在x轴下方也有图像,并且穿越了x轴,自然有交点。
学生 5:没有零点, f(-2)·f(1)=-2<0。
教师:这里也满足端点的函数值互异,怎么就没有零点呢?
教师:若类似于问题 4、问题 5,先画函数 f(x)=3x-x2在区间(-1,0)上的图像就难办了,我们就只能用端点的函数值互异,且满足在区间(-1,0)上函数有意义来判断了,请你再填写函数零点存在定理。
学生 6:若函数 y=f(x)在区间[a,b]上图像是连续不断的一条曲线,且有 f(a)·f(b)<0,则函数 y=f(x)在区间上(a,b)有零点。(教师同时板书)
教师:也就是说函数y=f(x)在闭区间上有定义,且满足端点的函数值互异,则在开区间上就有零点;但没有回答有多少个零点,是不是只有一个呢?如果端点的函数值同号,是不是就没有零点呢?请同学们课后去讨论一下这两个问题。
4.“巩固提升”环节的教学实录。
逐一提问三位学生回答“巩固提升”中的三个问题.(注:学生 7、8、9 均为优秀生)
学生 7:选 B。
教师:你是如何求解的?
学生7:当x≤0时,解方程x2+2x-3=0得x=-3或 x=1(舍去);当 x>0 时,解方程-2+1n x=0 得,x=e2。
教师:你能归纳一下本题的解题思路吗?
学生7:通过解方程求零点。(教师同时板书)
教师:函数零点问题,首先是考虑通过解方程求零点;同学们课后可以画出函数图像,观察其图像与x轴交点的个数求解。
学生 8:选 C。
教师:你是如何求解的?
学生8:根据函数零点存在定理,计算端点的函数值,f(1)=-4<0,f(2)=1n2-2<0,f(3)=1n3>0。
教师:你为什么不通过解方程求解呢?
学生8:方程1n x+2x-6=0解不了。
教师:我们把1n x+2x-6=0叫做超越方程(即超出我们能力范围内的方程);有同学会问,在其他区间内还可能有零点呀!请同学们看教材P88例1,教材中是通过列表分析函数 f(x)=1n x+2x-6 在(0,+∞)上是单增的;实际上,y=1n x与 y=2x-6在(0,+∞)上均单增,由“和函数”的单调性可知 f(x)=1n x+2x-6 在(0,+∞)上也单增。本题的解题思路是:利用端点函数值互异,估计零点的范围(常针对单调函数而言)。(教师同时板书)
学生9:好像是选B。
教师:你是如何思考的?能通过解方程求零点吗?能利用端点函数值互异,估计零点的范围吗?
学生9:超越方程不能解,不是单调函数,不好估计零点的范围。
教师:将方程ex-x3=0变形为ex=x3,方程实根的个数相当于函数y=ex与y=x3图像交点的个数。请同学们动手在同一直角坐标系中画这两个函数的图像。
学生画图,教师巡视。发现有些同学两个图像没有交点,有些同学只有一个交点,只有少数同学有两个交点,展示有两个交点的同学的解法。
教师:注意当 x=3 时,ex<x3;当 x=5 时,ex>x3;且在后面函数y=ex是“爆炸式增长”,所以两个图像交点个数为2,正确选C。本题的解题思路是:分成两个函数,利用两个函数图像交点个数得函数零点个数。
