初中几何证明解题规范的问题与方法探索

□ 海南省保亭思源实验学校 陈祖艳

许多学生认为几何证明是初中数学学习过程中很大的难点，特别是有时自己有思路但说不出，或者不会写推理过程，又或者好不容易写出来过程后又不规范，因此在数学考试中往往因为几何证明部分得分低始终得不到更高的分数。其实，初中几何证明的学习并不难，所考察的知识点也都是比较基础，但几何证明被作为初中数学中招考试的必考考点，主要是为了发展空间观念、培养几何直觉、感受几何与生活及其他学科之间的密切关系，对培养学生严密的逻辑思维和推理能力有着十分重要的作用。很多学生之所以学不好几何证明，很大部分的原因都是因为找不准方向，或者没有好的解题思路，不然就是没有规范解题过程。因此，只要找出几何证明解题的问题，对症使用解题方法，进而对规范的解题过程进行加强训练，提高几何得分率就不成问题。

一、初中生几何证明解题规范的问题

为了能够准确了解学生在几何证明过程中出现的问题，笔者进行了问卷调查，共发出问卷3286份，回收3231份，回收率达98.33%。调查结果显示，学生的几何证明解题很不规范，其状况不容乐观，主要有以下几个方面：

1.对题目中出现的符号语言、图形语言的专业术语不能够正确地理解，造成审题不清。比如，弄不清楚“因为”和“所以”或把求证当已知来用，步骤重复较多或漏步骤，再者出现文章式步骤的毛病：

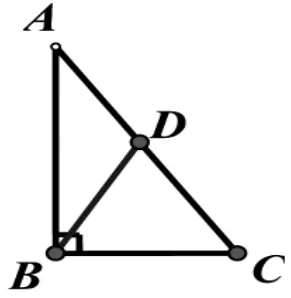
案例：如图，在△ABC中，∠ABC=90°，∠A=56°，CD=CB，求∠ABD 的度数？

不规范证明：∵∠ABC=90°，∠A=56°

∴180°-∠ABC-∠A=34°

∴∠C=34°

∵CD=CB

∴∠CDB=∠DBC

∵180°-∠C=∠CDB+∠BDC

∴∠CDB+∠DBC=146°

∴∠DBC=73°

∵∠ABC-∠DBC=∠ABD

∴∠ABD=17°

规范证明：∵∠ABC=90°，∠A=56°

∴∠C=180°-∠ABC-∠A=34°

∴∠C=34°

∵CD=CB

∴∠CDB=∠DBC=（180°-∠C）/2=（180°-34°）/2=73°（以下三句粗体字可合并写成这一句）

∵180°-∠C=∠DBC+∠BDC

∴∠CDB+∠DBC=146°

∴∠DBC=73°

∵∠ABC-∠DBC=∠ABD

∴∠ABD=17°

后面两句可以规范写成∴∠ABD=∠ABC-∠DBC=90°-73°=17°

2.对于题目中的条件不会联想或者不会用几何语言表达，也没有养成把条件标注在几何图形上的好习惯，语句比较混乱,造成书写不规范,主要表现在过程表达较为随意,不够严谨,常常出现多余的书写步骤或少写出必要的步骤,对图形、文字、符号三种语言的转换存在困难。比如下面的两个案例：

（1）一次性写出题目的条件，证明过程较乱。

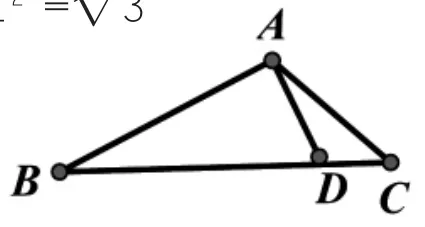
案例1：如图，在△ABC中，∠BAC=120°,∠B=30°,AD⊥AB,垂足为 A，CD=1c m，求 AB 长。

不规范解：在△ABC中

∵∠BAC=120°, ∠B=30°,AD⊥AB，CD=1cm（这里就是一次性写出题目条件）

∴AD=CD=1

∴BD=2AD=2

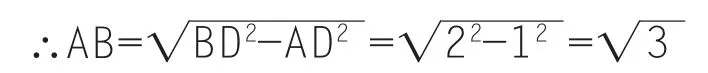
规范解:

∵AD⊥AB

∴∠DAB=90°

∴ ∠BDA=180°-∠DAB-∠B=180°-90°-30°=60°

∴∠C=∠BDA-∠DAC=60°-30°=30°

∴AD=CD=1

又 ∵∠BAC=120°，∠B=30°

∴∠DAC=∠BAC-∠DAB=120°-90°=30°

∴BD=2AD=2

在RT△ABD中

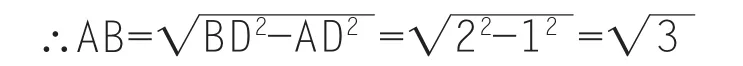
（2）缺少条件，证明过程不够严谨。

案例 2：如图所示，在四边形 ABCD 中，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是平行四边形吗？为什么？

不规范证明：∵BE∥DF，BE=DF

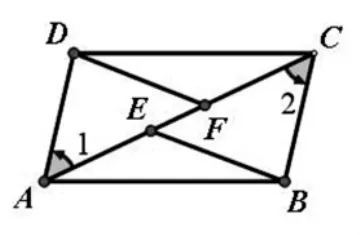
∴∠BEC=∠DFC

∴△AFD≌△CEB（SAS）

∴∠1=∠2

∴AD∥BC，AD=BC

∴四边形ABCD是平行四边形

规范证明：∵BE∥DF，BE=DF

∵AE=CF （粗体部分是学生缺漏的条件）

∴AE+EF=CF+EF

∴AF=CE

∴∠BEC=∠DFC

∴△AFD≌△CEB（SAS）

∴∠1=∠2

∴AD∥BC，AD=BC

∴四边形ABCD是平行四边形

（3）对几何的概念、性质定理、判定定理的识记混乱和理解流于表面,易忽略各定理适用的条件和范围和无法写出正确的根据。比如，没有根据的推理或根据不明确的案例：

如图，E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF。

求证：四边形ABCD是平行四边形。

不规范证明：∵AE=CF

∴AC平分▱ABCD

∴▱ABCD是平行四边形

规范证明：∵AE=CF

∴AE+EF=CF+EF

∴AF=CE

∵BE=DF

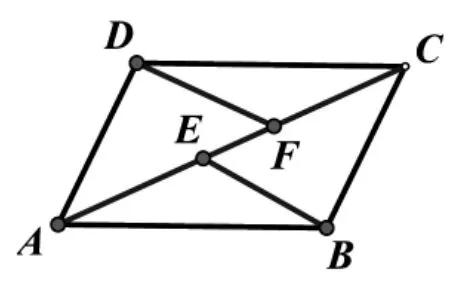
又∵BE∥DF

∴∠DFA=∠BEC

∴△DFA≌△BEC（SAS）

∴DA=BC,∠DAF=∠BCE

∴DA∥BC

∴▱ABCD是平行四边形

（4）对于需要借助添加辅助线来完成推理证明的题,感到无从下手,找不到连接题设与结论的桥梁，或找到但不在图形标注，在证明过程中不进行描述。比如，过程中有辅助线语句而图上没有画出辅助线的痕迹，或在证明解题过程时没有用几何语言写出辅助线语句。

案例：如图所示，在四边形 ABCD 中，E、F、G、H 分别是AB、BC、CD、DA的中点，则四边形EFGH是平行四边形吗？为什么？

解:四边形EFGH是平行四边形

理由如下：

连接BD（是学生不写但过程中有BD的）

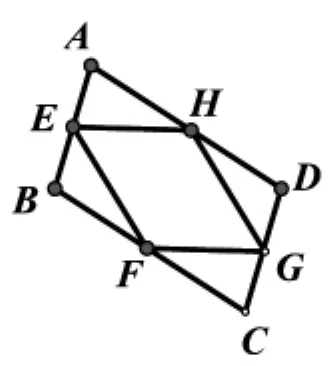
∵E、F、G、H 分别是 AB、BC、CD、DA 的中点

∴EH=BD,FG=BD

∵EH∥BD,FG∥BD

∴EH=FG,EH∥FG注意：图中也没有画出线段BD。

∴四边形EFGH是平行四边形

（5）对于文字证明题懒于画图，或是不会画图，或无法结合题意与图形,或不会找出已知条件和求证,导致不能正确写出证明过程。

（6）推理中逻辑上的错误导致书写证明过程出现循环论证、虚假理由、偷换命题。推理中逻辑上出现的书写错误的案例：

如图所示，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是平行四边形吗？为什么？

不规范解：∵E、F、G、H 分别是 AB、BC、CD、DA 的中点

∴AH=HD,AD=BC

∴▱EFGH是平行四边形

规范解：四边形EFGH是平行四边形

理由如下：连接BD

∵E、F、G、H 分 别 是 AB、BC、CD、DA 的中点

∴EH=BD,FG=BD

∵EH∥BD,FG∥BD

∴EH=FG,EH∥FG

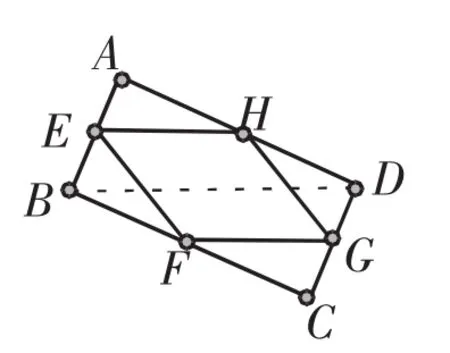
∴四边形EFGH是平行四边形

（7）在学习上遇到困难因为害羞或者是害怕同学嘲笑而没有及时地向老师、同学请教，造成知识上的盲点没有及时扫清。

面对学生出现的种种不规范解题的问题，教师需要敢于面对现实，努力改进教学方式、方法，从问题实际出发，把学生的练习、作业、试卷中具有针对性的解题不规范的问题收集并进行诊断，及时发现问题及时给予对症下药，扫除学生几何证明题解题不规范的问题。

二、初中几何证明规范解题的训练方法

1.牢固的几何知识基础是几何证明规范解题的奠基石。如直线、射线、线段、角等相关概念的学习，要让学生理解之后记住它，对点——线——角——三角形的表示法和画法、识图等加强练习和积累；能根据文字理解进行画图或根据简单图用几何语言表述，会识图，特别是可从训练简单图形到稍复杂的图形用几何语言书写出来。建议多做填空式证明题，教学中慢慢渗入数形结合的学习思想。

2.严谨的书写过程是几何证明规范解题的重要规则。特别是对“因为”和“所以”需要写入的是什么语句要有胸有成竹的把握，为了便于说明书写过程的规范，把“因为”和“所以”这一推理形式叫作一个二步推理。训练书写方法可以从以下几个方向入手：

（1）“因为”一般后面写的是题目中明显给出的直接可用条件，或者是上一个的二步推理的所得结论被当作下一个二步推理的条件，写入过程的“因为”中。

（2）“因为”后面还喜欢放入图形中隐藏的条件，如对顶角相等、全等的公共边和公共角、互余、互补等条件的几何语言。

（3）“因为”还可以放入一些题目给的不能马上推出想要的结论的间接条件语句，这时可能会需要几个二步推理，为下一轮的第二步推理创造必要条件，这时写法就可以把后两步的“因为”和前一个二步推理的“所以”两个语句合并成一个，也就是省略后两步的“因为”即可。而“所以”一般写的就是用“因为”推出来的结论。

（4）重点强调的是每一个二步推理不管是“因为”还是“所以”写入的语句都要有根据的，根据一般都是学习过的真命题，也就是定义、定理、公理等，初学者可以在语句后面用个括号写出这个根据，以便后面方便检查解题的过程是否严谨，合乎逻辑。

3.正确的逻辑思维是几何证明规范解题的支撑点。初中几何证明题解的思维一般有三种思维方式，在教学时可以训练学生灵活应用，对证明规范解题有很大的帮助：

（1）正向思维。几何证明过程逻辑思维培养从七年级课标中就有强调，体现在七年级下册就已经从一道道带填空的有“因为”和“所以”的几何语句串起来的半成品证明题目。不要小看这些填空证明题，它是训练学生已有一定的逻辑思维空间的正向思维训练，同时也可以检查学生逻辑思维，教师要把学生的几何思维通过这些空格把学生发散的思维有时带向集中，有时又要把集中思维带向发散，从而得到证明解题的正确思路，同时也初步得到几何证明规范解题的认识和训练。

（2）逆向思维。这是一种从题目的求证所提及的问题通过相反方向进行成功寻找思路的方法。运用逆向思维解题，能使学生从不同角度，不同方向思考问题，探索解题方法，从而拓宽学生的解题思路。

进入八年级从教材来看，前两章就开始进入真正的几何证明解题训练，特别是“证明三角形全等”的几何证明题对训练学生正确的逻辑思维有很大的帮助，学生通过对七年级下册的填空式证明题得到思维的初步训练，在八年级就可以进一步加强规范解题训练：

第一，书写严谨的证明过程：加强推理中的“因为”搭一个“所以”的搭档做法，提到“因为”放入什么语句，“所以”可以得到什么语句，根据是什么。

第二，不能丢弃的推理根据：每个“因为”和“所以”的推理不是无中生有的，而是有根有据的，要讲清理由和根据。理由和根据就是教材中学到的真命题，也就是定义、定理等。几何证明解题的根据，关键处解释方法是每次写证明过程时都让学生关注 “因为”和“所以”的前因后果和学生所学过的什么定理、定义等概念相符，其实也就是根据中所用的真命题（定理、定义等概念）的题设就是描述“因为”的几何语句，而结论就是描述“所以”的几何语句。简单说就是真命题的前部分是强调“因为”，后部分是支持“所以”成立的。

第三，串成一条线的逻辑思维：一个证明过程可能只用一个二步推理就得证，有时会用到几个二步推理才能得证，其中从一个二步到另一个二步的过渡有可能是后面的二步不够条件，要用到前一个二步推出的结果当作后一个二步推理的条件才行。

（3）正逆结合。对于从结论很难分析出思路的题目，学生可以结合结论和已知条件认真地分析，初中几何证明中，一般所给的已知条件都是解题过程中要用到的，所以可以从已知条件中寻找思路，这也是一条重要线索。当然解题解到一半没有思路了，也可以再从所遇到的问题入手找寻解决方法或从求证开始再逆推去找卡住的缓解方法。正逆结合还可以在用正向思维证明出来后，用逆向思维进行检查证明过程的正确性。

4.文字证明题是训练初中几何证明规范解题最完整版的体现。

八年级第二学期至九年级的几何证明题不断变化多向，综合性强，逻辑思维也不断升华，从一般证明题到文字证明题，还涉及反证证明题，这里重点说说文字证明题。文字证明题是没有图形、字母、数字，整个题目仅有文字。文字证明题要突破学生的审题——画图——写已知、求证——写证明过程的四环节训练。一个四环节过程下来需要写的东西很多，就如出题似的，因此做这类证明题，可以很好地训练学生的解题书写的功底，还可以训练学生数形结合思想的渗入能力。文字证明题的每一环节都很重要，通过审题理解后画出相应图形，再用字母正确标识，只要前面这两环节做得好，就能轻易和规范写出已知和求证，能把前三部分弄透弄懂，而规范的书写证明过程就事半功倍了。

5.培养科学的演绎推理和合情推理是几何证明规范解题的未来。就数学几何证明而言,演绎推理是证明解题用于证明数学结论、建立数学体系的重要思维过程。但数学结论、证明思路等的发现,主要靠合情推理。因此,学生要想掌握几何证明规范解题的各环节，教学中还要注意对这两种推理的初步渗透，这里不深入探讨。这两种推理的深入探讨在以后的高中几何证明学习也可以进行。

初中几何证明解题的规范问题不容忽视，要想提高学生的几何成绩，还需要对比问题，重视问题。