钢轨接头扭转对车辆-轨道动力学的影响研究
2018-09-20陈艳玮
陈艳玮,王 彪
(1.四川大学锦城学院,成都 611731; 2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)
在普速铁路中,由于轮轨关系复杂导致钢轨发生伤损病害的数量和类型众多,铁路道岔、曲线地段及钢轨接头被称为轨道结构中的三大薄弱环节[1-3]。在这其中,钢轨接头位置不平顺是引起钢轨接头区域轮轨冲击作用、轨道及车轮伤损病害、道床及路基残余变形加剧的根本原因[4-9]。目前,高速铁路轨道通常采用无缝线路,尽管通过钢轨焊接接头技术代替夹板技术消除了轨缝,但由于焊接工艺缺陷和长期运营中的伤损,使得钢轨接头区的不平顺仍然存在,并且对轨道和机车车辆的破坏、冲击噪声的产生等影响较大[10-14]。
无缝线路钢轨的焊接一般采用铝热焊接技术,其基本原理是将铝和铁的氧化物以及其他金属合金混合在一块,然后按照一定比例配置成铝热焊剂,将待焊钢轨对齐后,采用预热器进行预热,使用高温火柴点燃焊剂,释放大量的热量,高温钢水流入沙模和待焊钢轨组成的型腔中,熔化待焊钢轨端面,经冷却凝固最后实现钢轨焊接为一体[15-16]。然而,铝热焊接技术在钢水冷却凝固的过程中容易造成两侧待焊钢轨受力不均匀,进而造成接头区域内钢轨分别发生不同程度的扭转[17]。通过编制轮轨接触几何参数的计算程序及建立车辆-轨道耦合系统动力学模型,分别从静态轮轨接触点位置分布、接触几何参数及轮轨动力响应两方面研究焊接钢轨接头扭转对车辆-轨道动力学的影响。
1 钢轨接头扭转
焊接接头的轨顶面和轨头侧面平直度属严格控制指标,依据TB/T1632.1—2005《钢轨焊接第一部分:通用技术要求》中对焊接接头平直度的要求[18],对于设计速度大于200 km/h的线路,轨头工作面1m长度范围内,轨顶面垂直方向的最大偏差为0~0.2 mm,轨头侧面工作边水平方向的最大偏差为0~0.3 mm。焊接接头平顺度的测量方法是:纵向以轨顶面的纵向中心线为基准;横向以轨头侧面工作边上距轨顶面16 mm处的纵向线为基准。钢轨接头的几何不平顺通常使用SALIENT钢轨纵断面测量仪测量,其得到的不平顺是焊接接头区域存在的最大几何不平顺,但是无法准确反映车轮与钢轨真实接触点的位置变化情况。例如,如图1所示,两段钢轨之间通过焊接连接在一起时,由于铝热焊的作用,造成一端钢轨扭转-1/40,另一端钢轨扭转1/15,焊接接头长200 mm,本文规定钢轨向线路内侧扭转时为正,向线路外侧扭转时为负。

图1 钢轨接头扭转
如图1所示,焊接接头范围内,根据规范的测量方法和要求,其轨顶面垂直方向的最大偏差为0.06 mm,轨头侧面工作边水平方向的最大偏差为0 mm,符合规范的要求,但实际上钢轨已经在接头范围内发生了较大程度的扭转,势必会对车辆通过时的轮轨动力作用产生较大影响。
2 轮轨静态接触几何分析
基于迹线法原理编制轮轨静态接触几何参数的计算程序[19-20],钢轨接头发生扭转的区域内,如图1所示,一端钢轨扭转-1/40,另一端钢轨扭转1/15。车辆由钢轨扭转-1/40通往钢轨扭转1/15为正向通过,反之为反向通过,其方向规定如图2所示。

图2 轮轨坐标系规定
由图2可见,在轮轨静态接触分析和车辆动力学计算中,规定车辆正向通过时,右侧车轮与钢轨接头区域接触,相反,车辆反向通过时,左侧车轮则与钢轨接头区域接触。
2.1 轮轨接触点对
采用编制的静态轮轨接触几何计算程序,分别计算钢轨扭转-1/40和1/15时对应的轮轨接触点位置分布如图3所示。

图3 轮轨接触点位置分布
由图3可见,钢轨接头的扭转对轮轨接触点位置的影响很大,以无轮对横移时为例,轮轨接触点的位置由轨道内侧向轨道外侧偏移,横向偏移的距离约为25 mm。
2.2 车轮滚动圆半径差
车轮滚动圆半径差函数能反映轮对回复对中的能力,其计算公式如式(1),提取轮对横移0~12 mm范围内,车轮滚动圆半径差随里程变化的分布规律如图4所示。
ΔR=Rr-Rl(1)
式中,Rr为右侧车轮的滚动圆半径;Rl为左侧车轮的滚动圆半径。

图4 车轮滚动圆半径差
车轮对中时,左右车轮滚动圆半径相同,即相同时间内左右车轮前进的距离相同,此时轮对不会发生横向位移,当左右车轮滚动圆半径不同时,相同时间内左右车轮前进的距离发生差异,轮对在横向蠕滑力的作用下发生横向移动,且横向移动的方向偏向车轮滚动圆半径小的一侧。由图4可见,车辆正向通过时,车轮的滚动圆半径差大部分为正值,能够抑制轮对的横向位移,且相同轮对横移条件下,其滚动圆半径差越来越小,抑制轮对横向位移的能力越来越差;车辆反向通过时,车轮的滚动圆半径差大部分为负值,不能有效抑制轮对横向位移的同时还会加剧轮对的横向移动,在相同轮对横移的条件下,其滚动圆半径差越来越小。
3 车辆-轨道动力学分析
采用多体动力学软件SIMPACK建立车辆-轨道多体动力学模型[21-22],研究轮轨动力相互作用,车辆模型为32自由度整车模型,轨道结构考虑弹性支承,轮轨接触中法向采用赫兹理论,切向问题采用Kalker简化理论解决。仿真CRH2车辆以350 km/h速度正向和反向通过钢轨接头时的轮轨动力相互作用,车辆轴重为15 t,车辆模型其他计算参数见文献[23]。
3.1 轮轨接触点对
车辆正向通过和反向通过时,钢轨接头侧轮轨接触点位置的动态横向变化如图5所示。
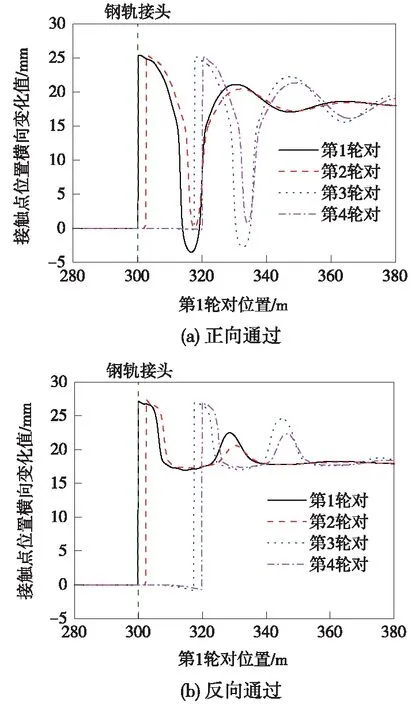
图5 接触点位置横向变化
由图5可见,车辆正向通过时,钢轨接头处轮轨接触点位置横向动态变化最大值为25 mm,由于轮轨接触点位置的变化,车轮通过焊接接头后,轮缘贴靠钢轨,轮对进而向反方向运动,形成较大幅度的蛇形运动;车辆反向通过时,钢轨接头处轮轨接触点位置横向动态变化最大值为27 mm,由于轮轨接触点位置横向接触不平顺幅值较大,会造成更大幅度的车辆蛇形运动。车辆正向通过和反向通过时,钢轨接头侧轮轨接触点位置的动态垂向变化如图6所示。
由图6可见,车辆正向通过钢轨接头时,轮轨接触点垂向位置首先发生下降趋势,幅值约为1 mm,易造成车轮减载;车辆反向通过钢轨接头时,轮轨接触点垂向位置首先发生上升趋势,幅值约为2.5 mm,易造成轮轨发生冲击增载。
3.2 轮轨力分析
车辆正向通过和反向通过时,钢轨接头侧轮轨横向力的动态变化如图7所示。
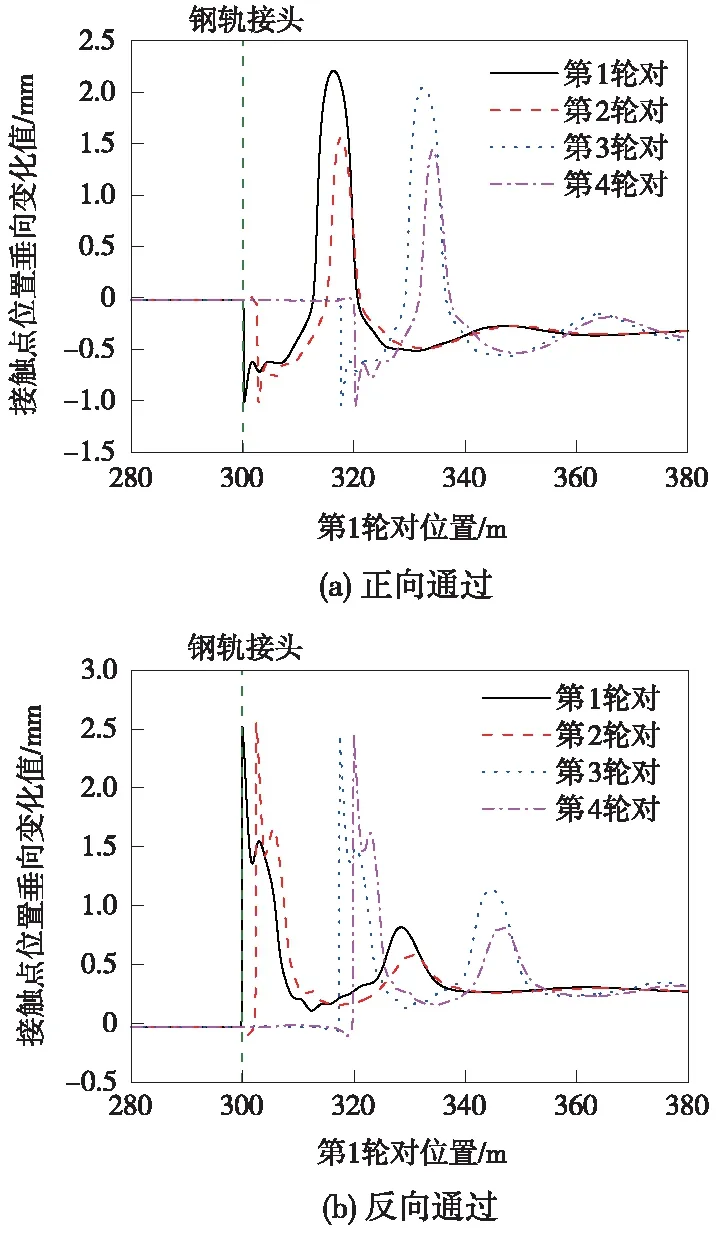
图6 接触点位置垂向变化
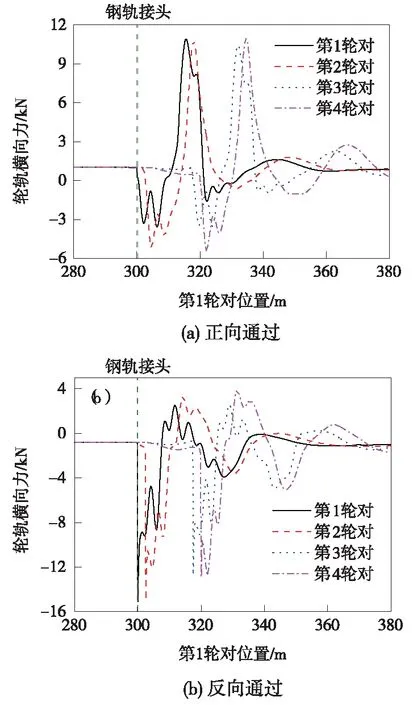
图7 轮轨横向力动态变化
由图7可见,车辆正向通过钢轨接头时,钢轨接头一侧轮轨横向力最大值为10.9 kN;车辆反向通过钢轨接头时,钢轨接头一侧轮轨横向力最大值为15.1 kN。相比车辆正向通过,反向通过时引发的轮轨横向力更大。车辆正向通过和反向通过时,钢轨接头侧轮轨垂向力的动态变化如图8所示。
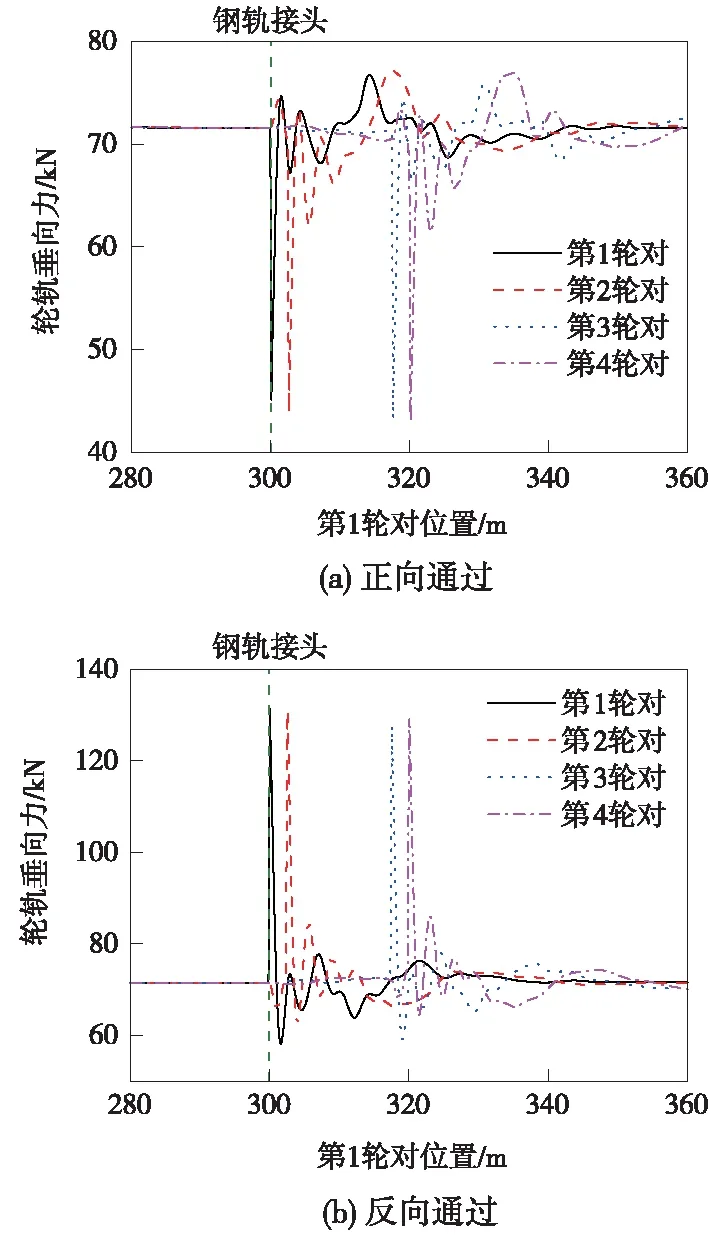
图8 轮轨垂向力动态变化
由图8可见,车辆正向通过钢轨接头时,钢轨接头一侧车轮主要呈减载的状态,最小轮轨垂向力为43.0 kN,最大垂向力为77.0 kN;车辆反向通过钢轨接头时,钢轨接头一侧车轮主要呈增载的状态,最小轮轨垂向力为58.2 kN,最大垂向力为131.5 kN。
4 结论
钢轨焊接过程中容易造成接头两端钢轨发生不同程度的扭转,这种扭转造成的轨道几何不平顺往往能够满足规范的要求,但实际的轮轨接触点位置已发生较大程度的改变,以焊接造成的钢轨扭转为研究对象,计算分析了钢轨扭转造成的轨道不平顺对轮轨接触几何参数和车辆轨道动力相互作用的影响。结论如下。
(1)钢轨接头的扭转对轮轨接触点位置的影响很大,无轮对横移时,钢轨扭转造成的轮轨接触点位置横向偏移量达到25 mm。
(2)车辆正向通过钢轨接头时,车轮的滚动圆半径差为正,能够抑制轮对的横移,相反,当车辆反向通过时,车轮的滚动圆半径差为负,不能有效抑制轮对横向位移的同时还会加剧轮对的横向移动。
(3)接头处钢轨扭转会极大恶化轮轨动力相互作用,反向通过时的轮轨动力相互作用大于正向通过时,轮轨横向力和垂向力的最大值分别高达15.1 kN和131.5 kN。
