基于改进FOA-SVM的冲击地压危险性等级预测

2018-09-20乔美英程鹏飞刘震震刘宇翔

中国地质灾害与防治学报 2018年4期

乔美英，程鹏飞，刘震震，刘宇翔

(1.河南理工大学电气工程与自动化学院，河南焦作 454000； 2.煤炭安全生产河南省协同创新中心，河南焦作 454000)

0 引言

随着煤矿开采深度的不断增加，冲击地压灾害日益频发，严重威胁着矿山安全。据统计，1985年我国有冲击地压矿井32个，而到2014年底，这一数字达到147个。2004～2014年间，我国冲击地压事故共造成三百余人死亡，上千人受伤[1]。因此，对冲击地压的危险性进行预测研究具有重要意义。

对冲击地压的预测，常用的有经验类比法和现场实测的电磁辐射法、钻屑法、地音与微震系统监测法等。这些传统方法在实践中取得了一定的成果，但由于井下地质条件和外部环境的复杂性、非线性和特殊性，采用单一指标预测有时会造成较大误差[2-4]。随着系统理论和人工智能的发展，已有学者在综合考虑地质条件和人工施工等多种因素影响下，建立起客观性和通用性更强的冲击地压模型，如多变量混沌时间序列模型[5]、AdaBoost集成神经网络[6]、Fisher 判别模型[7]、突变级数法[8]、广义回归神经网络(GRNN)预测模型[9]等。这些模型均具有自身的特点和优点，然而也存在着一些不足[10]：GRNN等网络模型预测精度较好，但泛化能力较弱；基于统计学理论的Fisher判别模型太过依赖样本的自身结构和数据的关联性；突变级数法的特点是避开了对指标采用权重，考虑了各评价指标的相对重要性，但存在着预测精度不够高的缺点。

支持向量机[11](Support Vector Machine，SVM)可以对冲击地压危险性评价的多种影响因素进行综合考虑，其非线性映射能力和泛化能力较好，且模型具有收敛速度快、预测精度较高、可重复训练等特性[12-13]。所以采用SVM对冲击地压等级进行预测，能较好地避免上述问题。

SVM模型的预测性能与参数的选择密切相关，目前对其参数的优化并没有统一的标准。果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)是一种基于果蝇觅食行为推演寻求全局优化的方法。具有计算简单、全局寻优能力较强的特点[14]，但与传统方法类似，FOA仍存在易陷入局部最优进而影响预测精度的缺点，在应对高维问题时更为明显。因此，本文提出一种改进的果蝇优化算法对SVM进行寻优：引入逃脱因子δ，摒弃固定的步长而采用递减的步长，步长随迭代次数的增加逐渐减小，并在三维空间中进行搜索。继而建立冲击地压危险性等级预测模型，进行仿真预测。

1 FOA-SVM模型理论

1.1 SVM基本原理

支持向量机(SVM)是由俄罗斯学者Vapnik提出的研究小样本、小概率和非线性事件的模型，其基本思想是以结构风险最小化为原则，通过非线性变换，将原空间的样本映射到高维空间中，然后在高维特征空间中构造出最优分类超平面[15]。xi∈Rd(i=1,2,…,N)表示样本向量，目标yi∈{-1,1}表示类别号,N为样本个数。寻求最优分类超平面的问题即转化为求解凸二次方程的问题：

(1)

其中，w和b是超平面方程f(x)=w·x+b的系数。引入松弛变量ξi，以提高学习方法的泛化能力，优化问题可表示为：

(2)

式中:C——惩罚因子，用于控制错分样本惩罚程度。

通过Lagrange乘子算法推导出上述问题的对偶形式：

(3)

式中:K(xi,xj)——支持向量机从低维空间向高维空间映射的核函数类型。常用的核函数有线性核函数、径向基核函数(Radial Basis Function,RBF)、多项式核函数和Sigmoid核函数。

因为RBF核函数只需确定一个参数σ即可，所以本文选用RBF核函数：

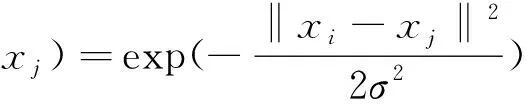
(4)

1.2 改进的FOA优化SVM模型

果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)是我国台湾学者潘文超[16]于2011年提出的群体智能算法。果蝇因其发达的视嗅觉能准确地找到很远的食物。通过模仿果蝇群体的觅食行为，FOA可以达到全局最优。果蝇群体发现食物的迭代过程如图1所示。

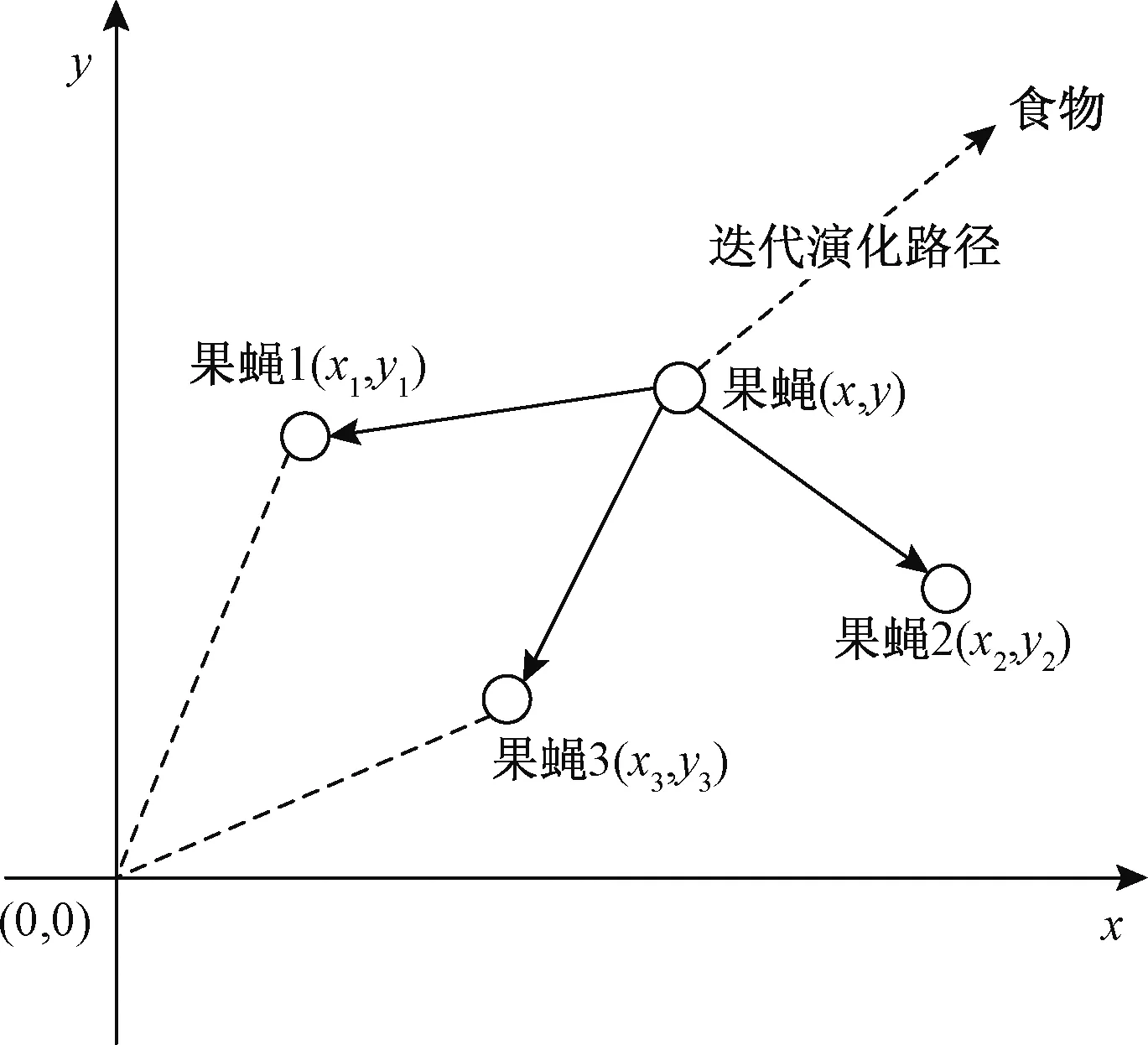
图1 果蝇群体迭代搜索食物示意图Fig. 1 Diagram of fruit flies iterative searching for food

SVM对非线性问题的分类性能主要取决于合适的核函数参数σ2和惩罚因子C[17]。在应用中，为方便起见，常将SVM的核函数参数σ2做变换如下：g=-1/2σ2，从而将g看作径向基核函数的参数进行研究。

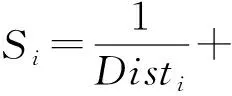
对于问题二，本文将固定的步长改为变化的自适应值，提出步长公式：

(5)

式中:imax——是迭代次数，

i——当前迭代次数，

R0——初始步长。

对于问题三，本文通过改进算法，使FOA在三维

空间中进行寻优。

利用改进的FOA算法对参数C和g进行寻优的步骤为：

,2,…n

(6)

式中:n——训练样本总个数;

xmin——输入数据中的最小值;

xmax——输入数据中的最大值。

步骤 2 主成分分析。因本文所选冲击地压数据特征为多变量，多变量之间往往具有一定的相关性，若不进行降维，可能导致样本信息过度重复。故进行主成分分析将原来具有一定相关性的特征量通过变换重新组合成一组新的互不相关的特征量以实现降维。

步骤 3 随机初始化果蝇群体位置区间,迭代果蝇搜寻食物的随机飞行方向和距离，设置种群规模和迭代次数。

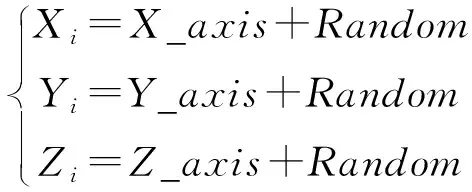
(7)

步骤4 计算果蝇距初始位置的距离，进而利用味道浓度判定函数求出味道浓度，对寻优参数C和g赋值。

(8)

(9)

C=20S(i,1)

(10)

g=S(i,2)

(11)

步骤5 将Si代入目标函数中，得到味道浓度判定值：

Smelli=FitnessFunction(Si)

(12)

步骤6 找寻果蝇群体中味道浓度最优的个体。

肌纤维组织切片封片后,使用倒置显微镜进行摄像,每组选6个样本，每个样本选取相似部位的3个切片进行相同视野的观察和分析；用Image-Pro Plus6.0图像分析软件进行定量，分别计算出I型肌纤维、Ⅱ型肌纤维的目标面积及其百分比。目标面积用积分光密度(integrated optical density, IOD)表示，再换算成肌纤维百分比。

步骤7 保留最佳味道浓度值及其坐标，果蝇群体通过视觉飞向该位置。

步骤8 迭代寻优。重复执行步骤3～7，并判断当前味道浓度是否优于前一迭代味道浓度，结束条件为寻优达到最大进化代数。

改进的FOA-SVM算法流程如图2所示。

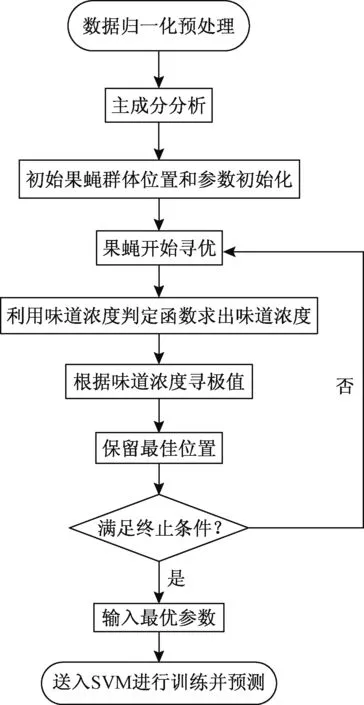
图2 改进FOA-SVM算法流程图Fig.2 Procedure of improved FOA-SVM

2 实验仿真及性能分析

为验证改进的FOA-SVM性能，选取3个常用的测试函数进行算法性能测试，求它们的极小值，并与其它方法进行比较。3个测试函数理论极值都为0，具体信息如下：

(1)Rastrigin函数：

(2)Griewank函数：

(3)Ackley函数：

分别采用FOA和改进FOA两种算法对测试函数进行测试，每个测试函数独立运行20次，表1给出了20次实验结果中的最差值(Max)、最优值(Min)、20次结果的平均值(Mean)以及标准差(Std)。图3给出3个测试函数的适应度迭代寻优曲线(为便于观察，对适应度取以10为底的对数)。

表1 两种算法测试结果比较

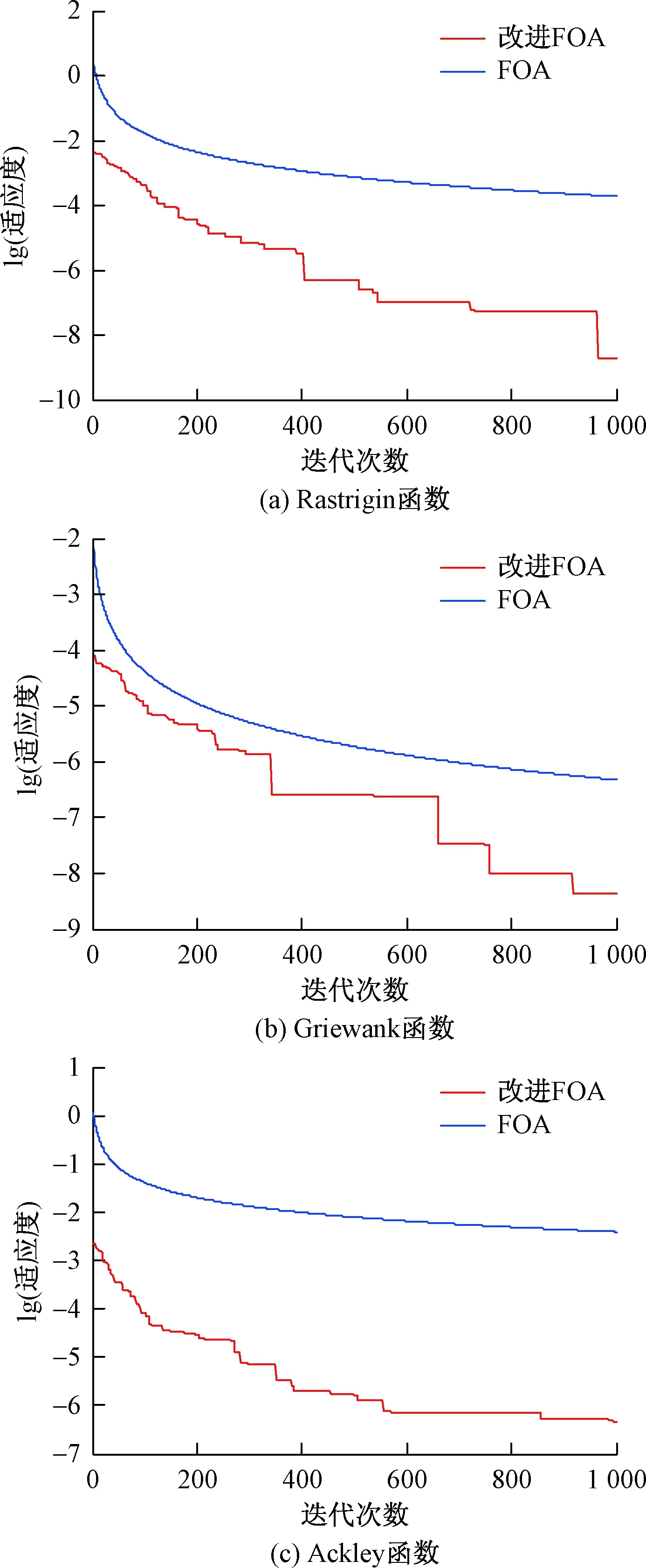
图3 2种算法对3个测试函数的迭代曲线Fig.3 The iterative curve of 2 algorithms for 3 test functions

从表1可以看到，对于Rastrigin、Griewank、Ackley 3个常见的测试函数，改进FOA的最差值、最优值、20次结果的平均值和标准差几乎都要优于FOA，函数Rastrigin和Griewank的最优值相比标准FOA提高了10个和7个数量级。从图3的收敛曲线也可以看到，标准FOA容易陷入局部最优无法跳出，致使收敛精度不够；而改进的FOA可以跳出局部最优并进行全局搜索，收敛精度更高。

3 工程应用实例

3.1 影响冲击地压判别参数的选取

影响冲击地压发生的因素很多，且具有不确定性和模糊性。冲击地压的发生往往是多因素共同作用的结果。所以,要在冲击地压预测中要取得好的效果，必须先确定主要影响因素。根据煤矿地质构造及开采方式，结合有关冲击地压等级评判体系[19]，影响冲击地压发生的因素主要有：煤层厚度、倾角、埋深、瓦斯浓度、构造情况、倾角变化、煤厚变化、顶板管理、卸压和响煤炮声等十个方面。其中前四项采用实测值直接输入；后六个参数属于状态参量，需要对其作数量化处理，赋值规则见表2[20]。

表2 冲击地压危险性指标赋值规则

3.2 改进的FOA-SVM模型应用

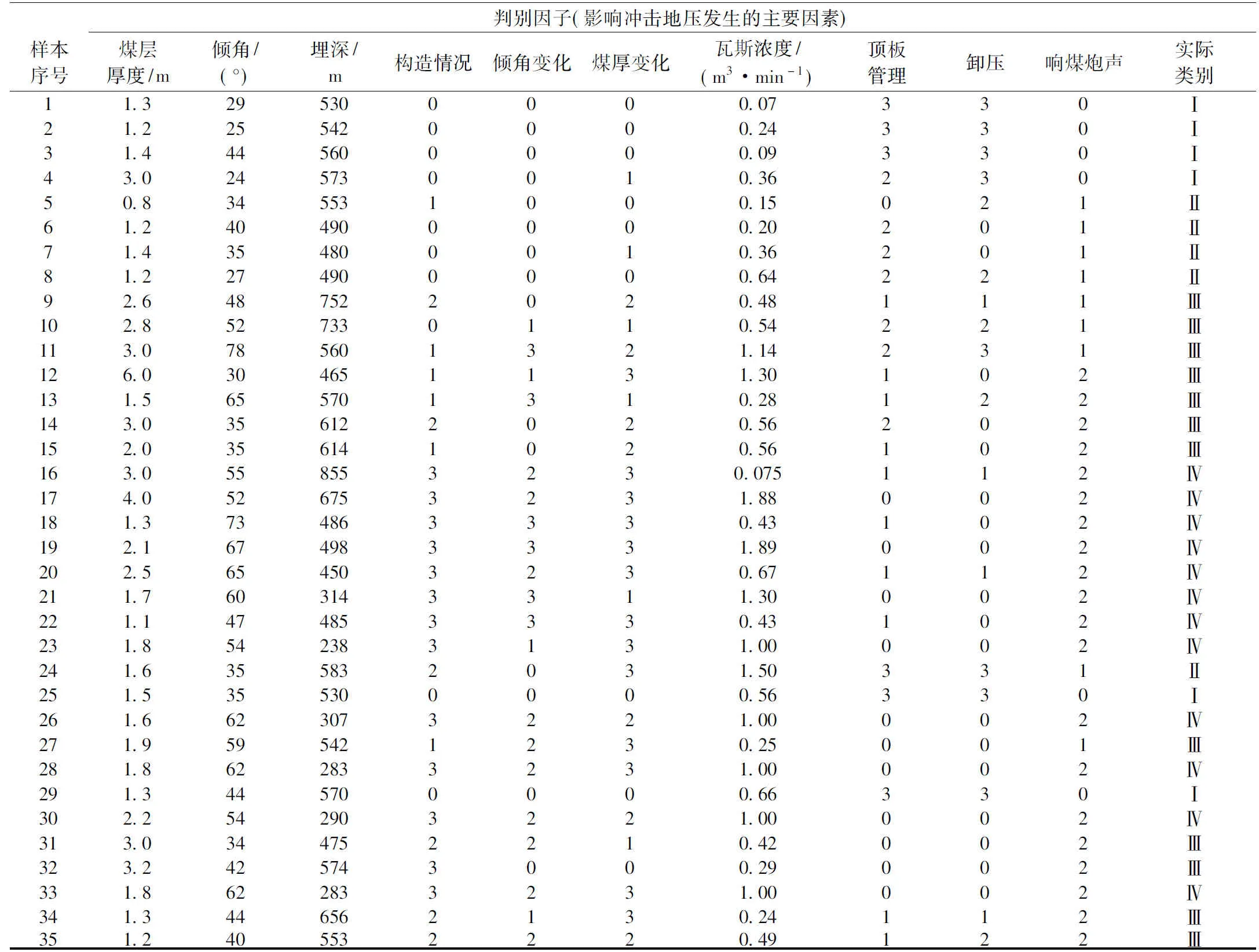
砚石台矿位于四川盆地，曾多次发生冲击地压事故。以文献[7]提供的砚石台矿35组历年冲击地压数据为例。评价结果分为4个等级：1、无冲击危险；2、弱冲击危险；3、中等冲击危险；4、强冲击危险。并分别用Ⅰ、Ⅱ、Ⅲ、Ⅳ表示四个等级。冲击地压样本数据统计情况见表3，其中，前23组为训练集，后12组为测试集。

利用Matlab2010b和SVM-SteveGunn工具箱进行编程，创建改进的FOA-SVM模型。

首先，对样本数据进行归一化预处理，参照公式6利用线性函数变换将原始样本归一化到[0,1]区间。

其次，对归一化后的数据进行主成分分析，得到降维后的新数据样本如图4所示。从图4中可以看到，前7个参数的累计贡献率已经达到97%。所以，原数据样本的训练集和测试集分别由23×10和12×10降为23×7和12×7矩阵。

图4 样本特征量主成分分析贡献率图Fig.4 The PCA contribution rate chart of sample characteristic quantity

然后，利用前23组冲击地压数据训练模型，对最后12组数据进行预测。FOA初始化果蝇群体位置区间[0,1],迭代果蝇搜寻食物的随机飞行方向和距离[-10，10]，种群规模20，迭代次数100，C的搜索范围设为[0，100]，g的搜索范围为[0，1 000][21]。100次迭代后的适应度收敛情况如图5所示。

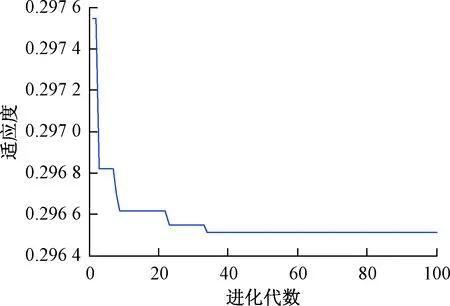
图5 改进的FOA-SVM寻优迭代代数曲线Fig.5 Iterative algebraic curve of improved FOA-SVM

由图5可知，经过34次迭代后，种群的最佳适应度保持稳定，可认为达到最优解，此时bestC=0.852 4，g=0.097 6，将最佳C和g代入SVM中，得到训练和预测结果如图6所示。

图6 改进的FOA -SVM测试结果Fig.6 The testing results of improved FOA -SVM

图6(a)为23组训练数据的训练结果，(b)为12组测试数据的预测结果。“*”为真实值，“。”为预测值。从图中可以看出，训练集的模型误判率为0，测试集只有第一个样本预测错误，其他11个样本全部正确。预测正确率达到 91.67%，程序运行时间为21.61 s。

为验证改进的FOA-SVM模型优越性，使用标准FOA-SVM、PSO-SVM和GA-SVM模型分别对冲击地压危险性等级进行预测，预测结果如图7所示。

图7 3种方法预测结果Fig.7 The testing results of 3 methods

从图7可以看出，PSO-SVM和GA-SVM两种方法的预测结果分别有两个样本点预测错误(PSO-SVM模型为样本1和样本8，GA-SVM模型为样本1和样本11)，预测正确率达到 83.33%，PSO-SVM模型程序运行时间为3.31 s，bestC=3.21，g=0.33；GA-SVM程序运行时间为2.13 s，bestC=7.94，g=0.20。标准FOA-SVM模型在第一个样本点预测错误，运行时间为29.74 s，bestC=2.73，g=0.14。可以看出，改进FOA-SVM的预测结果明显优于PSO-SVM和GA-SVM，但因样本数有限，未能在本实例中明显体现出优于标准FOA-SVM的预测能力，但可以看到改进FOA-SVM的效率还是高于标准FOA-SVM的。

至于为何4种模型都在预测测试集的第一个样本时错误，笔者采用局部敏感性分析法，即：将测试集样本1中的因素逐个减少或改变，代入模型预测。结果表明煤厚变化和卸压方式是影响样本1误判的主要因素。之前因样本1中瓦斯浓度数值与其它样本中同一危险性等级的瓦斯浓度值相差较大而怀疑瓦斯浓度也可能是造成样本1预测错误的一个因素，但结果表明瓦斯浓度对结果影响并不大。当然，具体精确的原因还需更加深入的研究。