水力滞回性对降雨入渗边坡稳定性的影响

孟庆成，王 明，齐 欣，魏 鑫，张梦宇

(1. 西南石油大学土木工程与建筑学院，四川 成都 610500；2.西南交通大学土木工程学院，四川 成都 610031)

0 引言

边坡非饱和土在受到季节性的降雨、蒸发循环影响后，常出现边坡失稳，导致滑坡、泥石流等自然灾害，造成巨大的损失。目前对非饱和土的研究大多是以土水特性曲线(Soil Water Characteristic Curve，以下简称SWCC，即基质吸力与含水率的关系)为基础，土中含水量在脱湿过程中随着基质吸力的增加而减小，在吸湿过程中随着基质吸力的减小而增大。脱湿曲线和吸湿曲线通常不唯一，这种现象称为水力滞回现象[1]。尽管水力滞回现象客观存在，但目前实际工程中一般都不考虑水力滞回特性，默认脱湿曲线与吸湿曲线重合。

通常，学者研究的都是降雨作用对边坡的影响，但是在实际情况中边坡受到的是不断变化的天气，属于干湿循环作用。“干”是指边坡受到日照蒸发，土体中含水量减少，发生收缩；“湿”是指边坡受到降雨湿润，坡内土壤含水量增加，基质吸力降低，土体趋向饱和，土壤因为吸水浸泡而软化，抗剪强度随之降低。交替的降雨和蒸发作用对土体产生了干湿循环作用[2]。该作用不但影响土体中的水分含量、分布状况，也会改变基质吸力的大小，引起变形，从而改变土体的微观结构，影响土体的强度特性，进而促使边坡的稳定性发生变化。

目前，研究水力滞回性对降雨入渗边坡稳定性的文章较少。且已有的水力滞回性对降雨入渗边坡稳定性分析的文章中的观点也不尽相同，其中，高玉坤[3]研究了干湿循环下非饱和土边坡的响应，认为考虑水力滞回性对干湿循环下边坡稳定性的影响很小，可忽略不计；Tami等[4]研究了具有迟滞性SWCC的土壤柱吸力分布的变化，发现由于滞后，一段时间的渗透后新达到稳态的吸力受到渗透过程前初始含水量的显着影响；Yang等[5]研究了在蒸发和降雨循环作用下土柱中基质吸力和体积含水率的变化，考虑水力滞回特性时，计算结果更接近实验结果。近几年，水力滞回性对土壤边坡稳定性的影响得到了重视，Ebel等[6]提出，忽略滞回性的模拟可能会低估滑坡的可能性；Ma等[7]对土体边坡进行了实验和数值研究，以评估滞后效应对水力响应和边坡稳定性的影响，计算得的考虑水力滞回性的边坡安全系数在降雨之后恢复的更快一些，在任一时刻都比不考虑水力滞回性的模型安全系数要更高。

由于对非饱和土强度特性的干湿循环效应缺乏系统全面的研究，现有的非饱和土边坡稳定性分析理论通常只考虑吸力对强度的贡献，忽略干湿循环对非饱和土强度的影响，考虑水力滞回性的研究更是少之又少,边坡又经常在经历多次降雨、蒸发过程后失稳。如果不考虑土水特性曲线中的水力滞回现象，边坡的安全系数有可能被低估。因此，研究降雨蒸发循环过程中水力滞回性对边坡稳定性的影响具有重要意义。本文依托ABQUS软件，研究降雨、蒸发循环过程中水力滞回性非饱和土边坡稳定性的影响，为边坡稳定分析提供依据和参考。

1 基于流固耦合的非饱和边坡稳定分析

为开展降雨-蒸发循环条件下边坡稳定性分析，基于Biot固结理论直接耦合的方法[8]，考虑非饱和渗流场与应力场之间的相互耦合作用，忽略气体压力、压缩性和温度变化的影响，以小变形为前提条件，利用虚功原理和有效应力原理，在应力应变关系和渗流规律基础上，进行有限元离散，建立耦合数学模型。

边坡稳定分析有极限平衡法和数值方法等[9]，本文采用有限元强度折减法。定义强度折减系数Fr为场变量，土体强度随之变化，在分析中对Fr线性增加，达到强度参数不断减小的目的，直至模型不收敛，按照失稳评价标准确定安全系数[10]。

折减后的抗剪强度参数可以表示为：

(1)

式中:c、φ——土体抗剪强度指标；

cm、φm——维持平衡所需要的抗剪强度；

Fr——强度折减系数。

2 有限元模型

2.1 几何及边界条件

计算采用Mohr-Coulomb破坏准则[11]。模型采用CPE4P单元。水平、竖直方向施加位移约束，左右两侧施加水平约束。边坡和顶部为透水边界，底部边界为不透水边界。利用Distrubution空间分布函数在左右两侧水位以下的边界上设置随深度线性增加的静水孔压，并在降雨入渗分析步中将坡脚面(即DE面)的孔压设为0，其余边界不设置排水边界。模型受到重力荷载外和边坡及坡顶幅值变化的降雨、蒸发作用。有限元模型如图1所示。

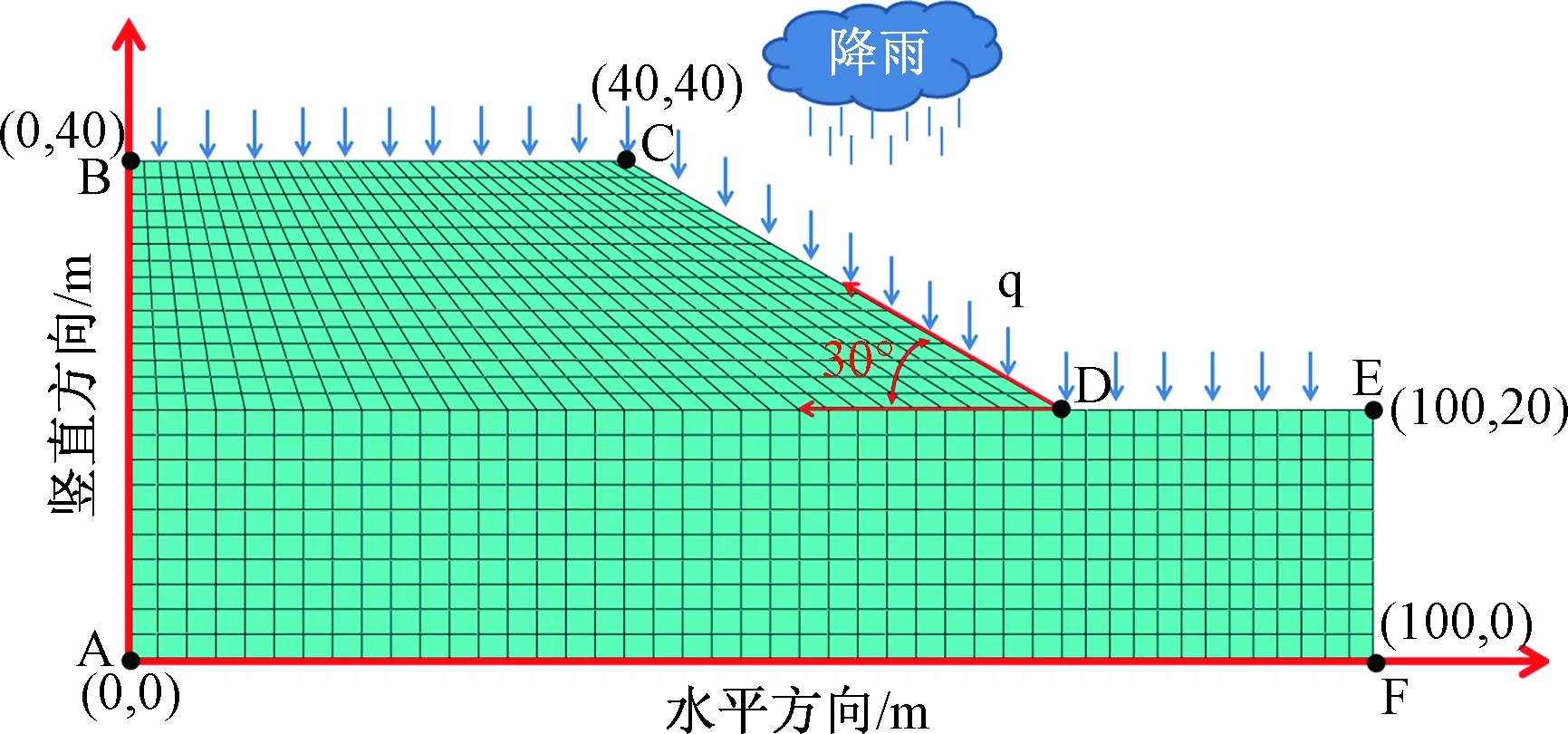
图1 有限元模型示意图Fig.1 Finite element model sketch map

2.2 水土特性方程

模拟土体渗流时，饱和度与基质吸力之间的关系采用了ABQUS中的土水特性曲线数学模型(式3～4)，其中的参数A、B、S0、S1的取值见表1。将四个参数代入土水特性曲线方程后，可得图2基准土水特性曲线。

≤S<1(3)

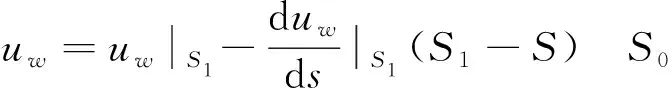
表1 土水特性曲线参数Table 1 Soil-water characteristic curve parameter

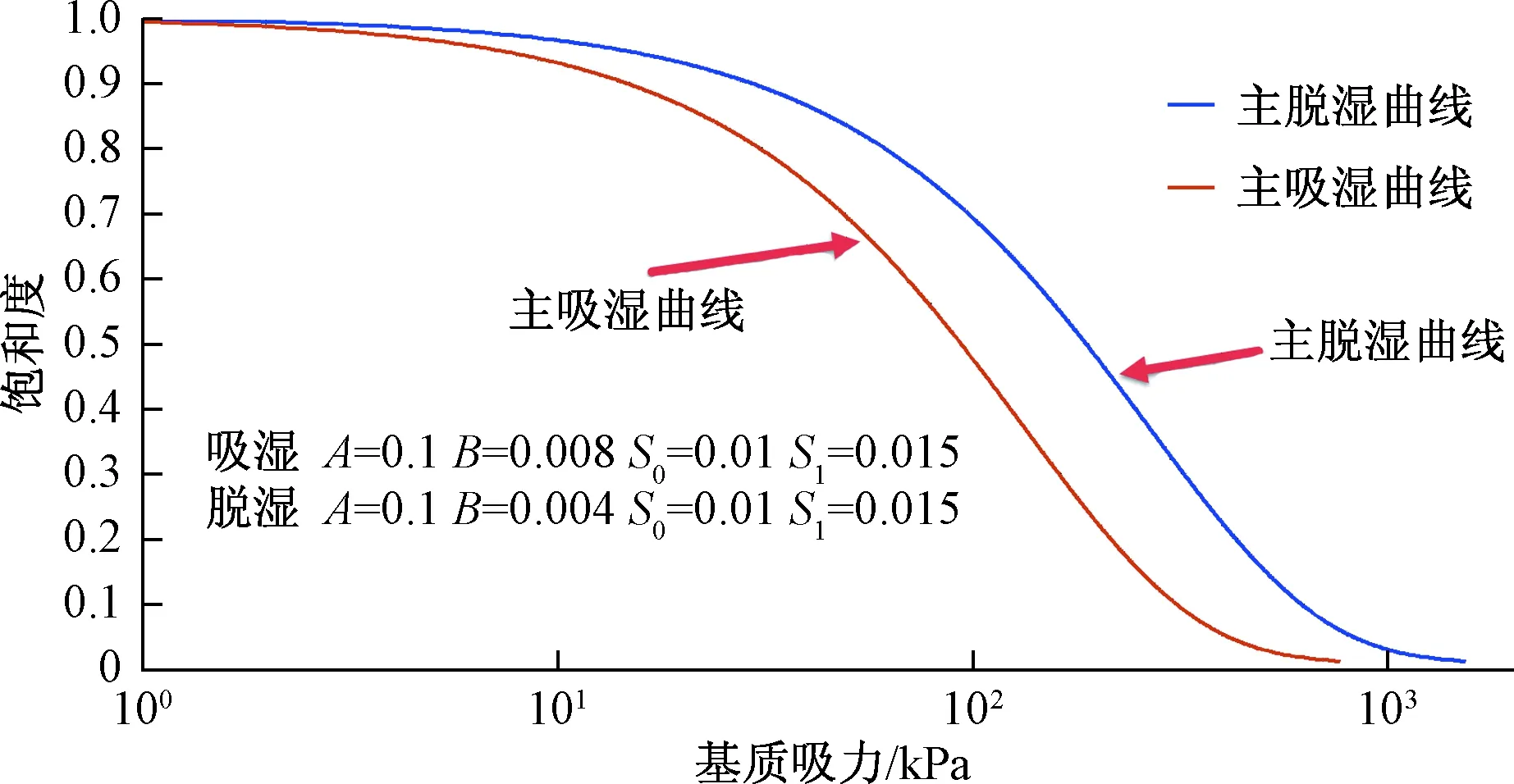
图2 基准土水特性曲线Fig.2 Baseline soil-water characteristic curve

模拟土体渗流时渗透系数采用由LEONG和RAHARDJO提出的指数公式[12]：

(5)

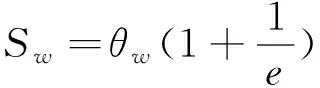
式中：e——土壤孔隙比，取为1；

Sw——土壤饱和度；

Sr——残余饱和度，取为0.01；

Ss——最大饱和度，取为1；

ks——是饱和时的渗透系数；

p——由土体种类决定的一个常数。

如果p的大小在研究的斜坡范围内不发生变化，那渗透系数函数的不确定性将由p确定，取p=1。材料参数选择见表2。

表2 材料参数

2.3 降雨蒸发条件

我国的气象部门降雨强度标准见表3。

表3 降雨强度参数Table 3 Rainfall intensity parameters

为模拟极端天气，竖向降雨强度取为qv=20 mm/h，即特大暴雨。斜坡面上降雨入渗强度根据坡面角度折减q=qv×cos30°=17.3 mm/h。降雨、蒸发强度随时间的变化关系如图3所示。

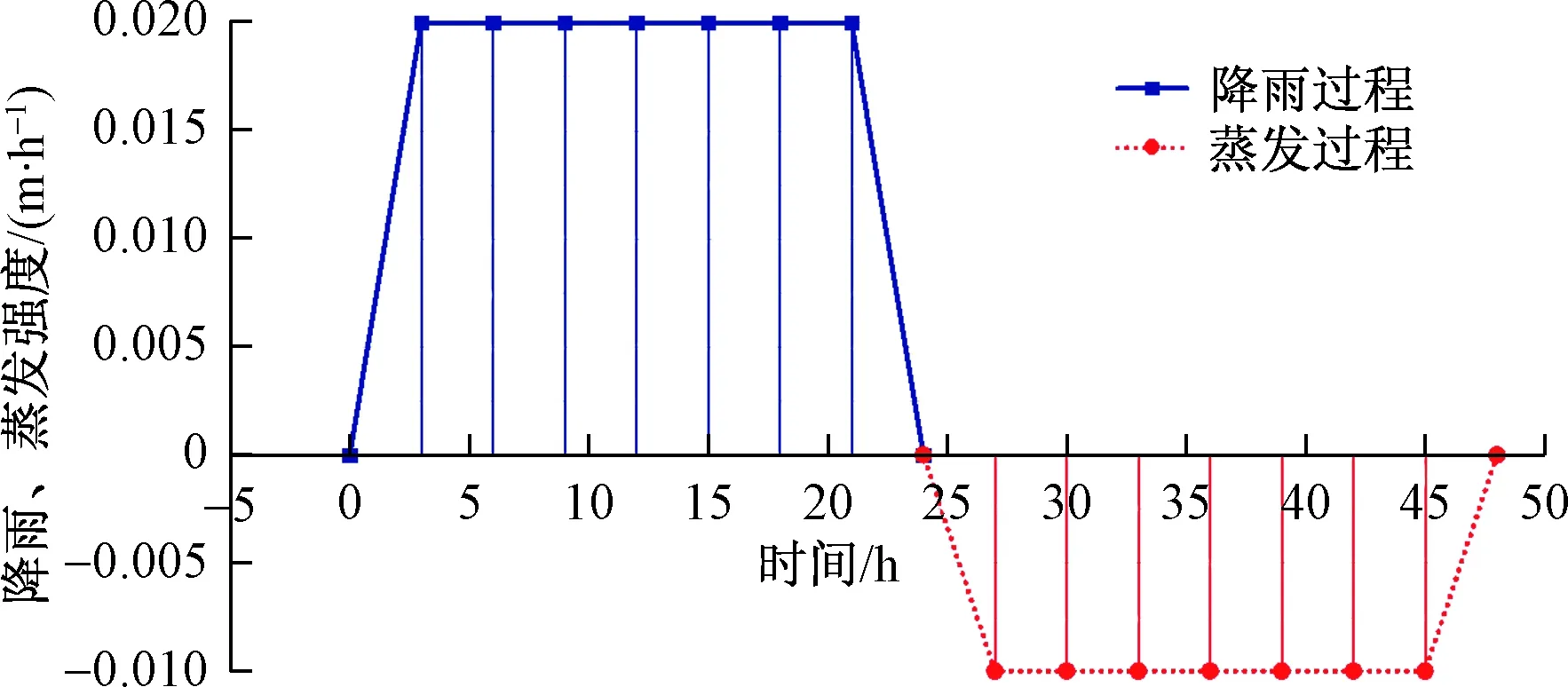
图3 降雨、蒸发模式Fig.3 Rainfall and evaporation models

2.4 初始状态的建立

初始地应力对最终分析结果影响较大，且土体材料刚度等往往与初始应力状态相关，因此，初始应力场平衡是正确模拟岩土工程的基础[13]。本文在进行后续分析前，经过6次迭代平衡地应力，所得的土坡降雨、蒸发之前的位移分布云图(图4)，位移的数量级达到了10-10m级。已达到足够精度要求，初始地应力平衡结果对后续的分析工作影响可忽略。

图4 位移云图(迭代6次之后)Fig.4 Displacement nephogram(after six iterations)

3 结果分析

为了研究水力滞回性对降雨、蒸发条件下边坡稳定性的影响，分别考察不同时刻边坡内部孔隙水压力、位移等的发展规律，从而最终对安全系数进行分析。

实验室中相比主吸湿曲线，主脱湿曲线更容易测得，因此，以下分析对比考虑了水力滞回性的模型(Hysteresis Model,以下简称HM)和仅用主脱湿曲线代替土水特性曲线的不考虑水力滞回性模型(Drying Curve—Non-hysteresis Model，以下简称D-NHM)两者结果。

3. 1 孔隙水压力变化规律

随着降雨过程雨水不断均匀入渗，边坡各个位置的孔隙水压力逐渐增大，而上部非饱和区的基质吸力不断减小，基质吸力为孔隙气压力和孔隙水压力差值，在降雨过程的结束阶段随着孔隙水压力消散，非饱和区尤其是顶部附近的基质吸力会略有恢复；蒸发阶段，基质吸力随着水分的蒸发而不断增大。图5为12 h、24 h、36 h、48 h时间节点处孔隙水压力分布云图，左列为考虑水力滞回性模型(HM)所得的结果，右列为仅用脱湿曲线代替SWCC曲线的模型(D-NHM)结果。

由图5可得，在降雨阶段，考虑了水力滞回性的模型(HM)基质吸力总是大于不考虑水力滞回性的模型(D-NHM)，在降雨阶段减小的速度要小于不考虑水力滞回性的模型(D-NHM)；在蒸发阶段，HM模型基质吸力相比D-NHM模型恢复速度更快。整个干湿循环过程中，HM模型的基质吸力的变化范围大于D-NHM模型。

同时做出用主吸湿曲线代替土水特性曲线的不考虑水力滞回性模型(Wetting Curve-Non-hysteresis Model，以下简称W-NHM)，对比HM、D-NHM和W-NHM的孔隙水压力与时间曲线(图6)。可以看出，在降雨阶段，HM模型与W-NHM模型比较接近，均大于D-NHM的基质吸力。在蒸发阶段，D-NHM模型与W-NHM模型孔隙水压力曲线接近，远小于HM模型，在降雨、蒸发过程结束后，HM在基质吸力几乎是其余两模型的两倍。因此，水力滞回性对降雨入渗边坡孔隙水压力的变化有很大的影响。

3. 2 位移变化规律

边坡稳定性研究，其变化运动趋势最终将综合反映在边坡位移上，图7(a)-(d)给出了HM和D-NHM模型每隔12 h的位移矢量分布。

由图7可知，D-NHM模型在降雨阶段坡肩位移较大，而坡脚处位移比较小；边坡顶部表现出一定的膨胀性，这主要是由于随着雨水渗入坡体导致边坡饱和度不断增大，基质吸力降低，有效应力减小，出现“卸荷回弹”现象。随着降雨强度不断减小至停止，孔隙水压力逐渐消散，坡肩回弹，坡顶的膨胀消失。这可以解释边坡滑坡一般首先是在坡肩出现裂隙，然后在坡脚处发生滑移的现象。而HM模型则没有那么明显。

同时考察HM、D-NHM和W-NHM模型的坡脚位移随时间的变化(图8)，在降雨阶段，三个模型的差异不大，HM模型与W-NHM模型基本重合，D-NHM模型的位移稍大；进入到蒸发阶段，HM模型体现出明显的不同，其位移远大于另不考虑水力滞回性的另两个模型，无论是D-NHM模型还是W-NHM模型，其位移变化较小，但HM模型位移变化的速率明显加快。降雨、蒸发过程结束后，HM模型的水平位移已达到D-NHM和W-NHM的两倍。

3. 3 安全系数变化规律

边坡稳定安全系数是研究边坡稳定性定量评价的主要依据之一，对于预防滑坡具有重要意义。

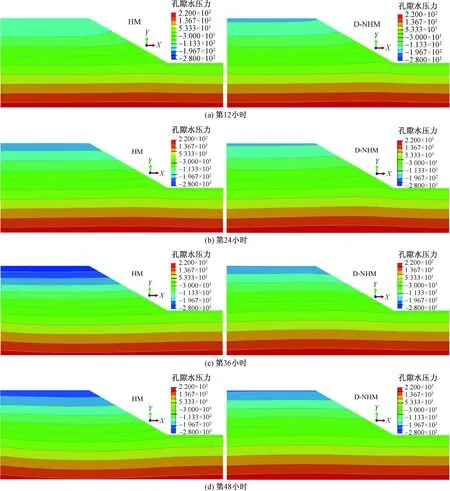
图5 孔隙水压力随时间变化Fig.5 Changes of the pore-water pressure with time

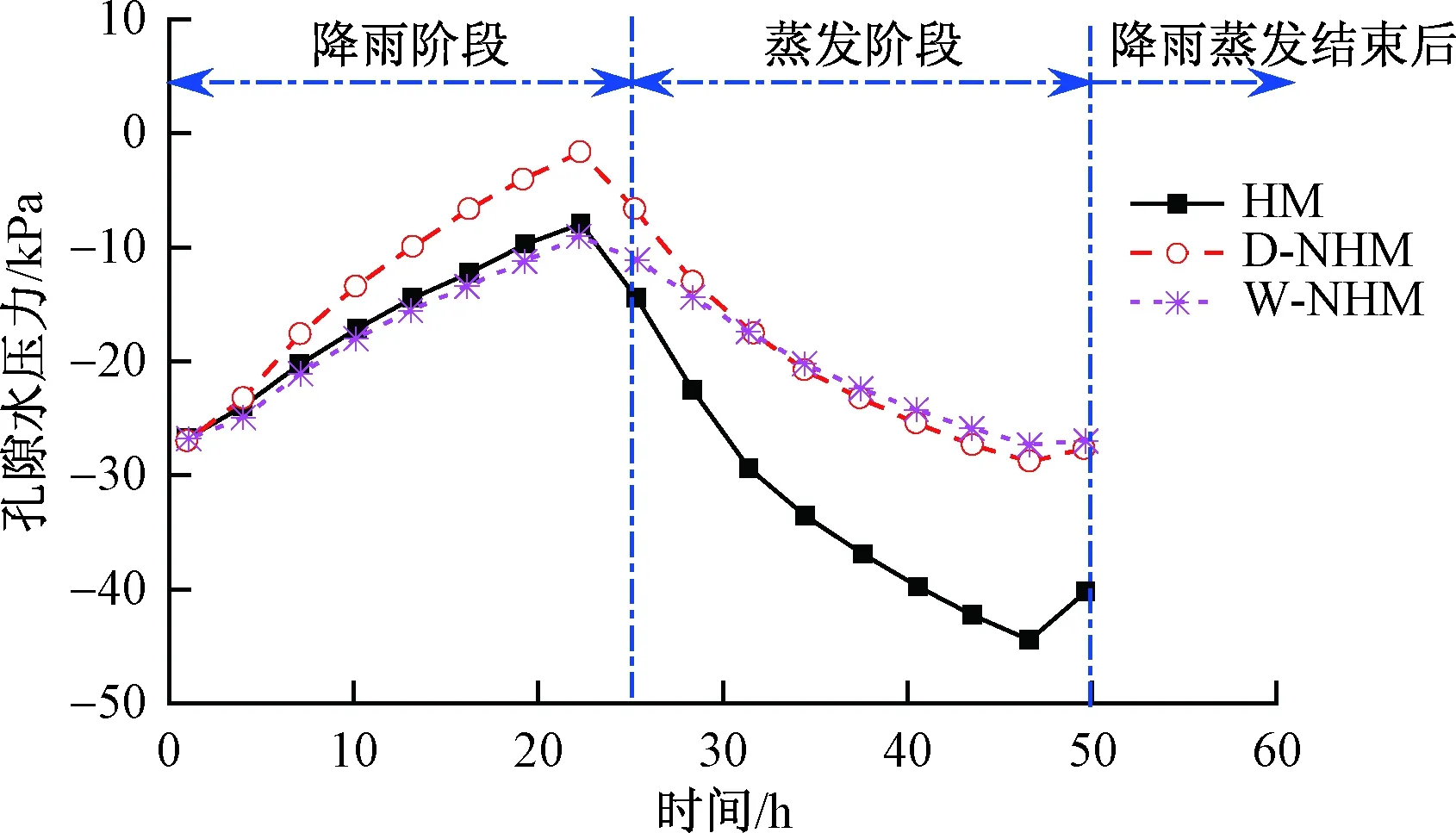
图6 孔隙水压力-时间曲线Fig.6 Pore water pressure-time curves

分别作出HM、D-NHM和W-NHM模型的安全系数与水平位移关系曲线 (图9)。当位移出现较大拐点时，认为边坡处于破坏的临界状态[14]，可看出考虑了HM的模型安全系数为1.362 5，D-NHM模型安全系数为1.489，W-NHM模型安全系数为1.536，即考虑水力滞回性的模型安全系数相比不考虑水力滞回性的模型更小。换言之，不考虑水力滞回性的模型高估了边坡的可靠性。

4 结论

(1) 在降雨阶段，HM模型基质吸力总是大于D-NHM模型和W-NHM模型，且减小的速度偏小；在蒸发阶段，HM基质吸力相比D-NHM恢复速度更快。整个干湿循环过程中，HM模型的基质吸力的变化范围大于D-NHM模型。在降雨、蒸发过程中，D-NHM与W-NHM模型体现出一致的变化趋势，但与HM模型明显不同，尤其在蒸发阶段区别明显；降雨、蒸发结束后，HM在基质吸力几乎是D-NHM、W-NHM模型的两倍。

图7 位移矢量分布Fig.7 Displacement vector distribution

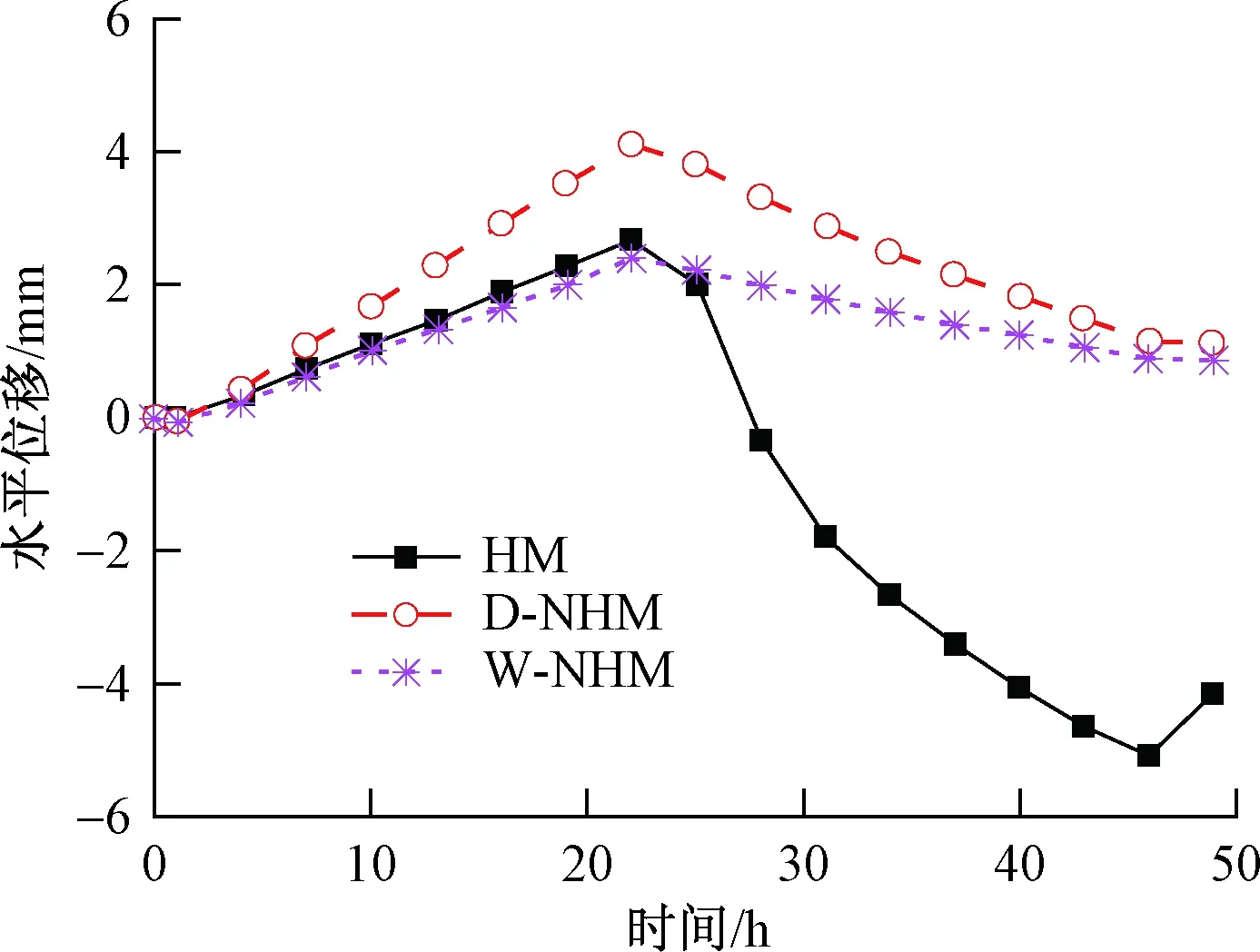
图8 坡脚位移-时间曲线Fig.8 Displacement-time curves at the slope toe

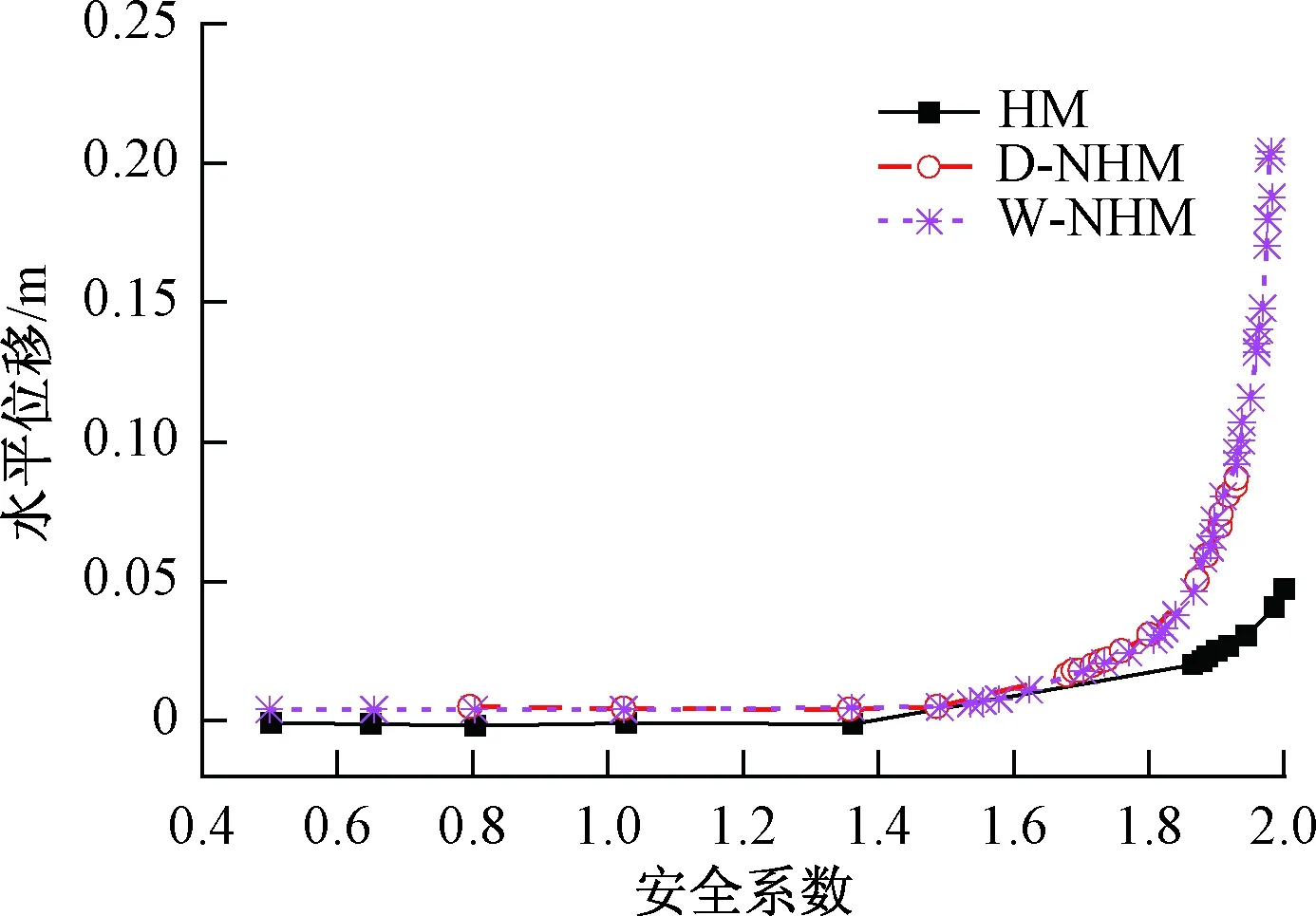
图9 安全系数-水平位移曲线Fig.9 Safety factor-displacement curves

(2)D-NHM模型在降雨阶段坡肩位移较大，而坡脚处位移比较小。无论是D-NHM模型还是W-NHM模型，其位移变化较小，但HM模型位移变化的速率明显加快。降雨、蒸发过程结束后，HM模型的水平位移已达到D-NHM和W-NHM的两倍。

(3)在降雨、蒸发条件下，水力滞回性导致边坡安全系数的改变。HM的安全系数为1.362 5，D-NHM的安全系数为1.489，W-NHM的安全系数为1.536。相比HM的安全系数，D-NHM的安全系数高估了9.28%，W-NHM的安全系数高估了12.73%。因此，水力滞回性对降雨入渗边坡稳定性有很大的影响，不考虑水力滞回性的边坡安全性被高估。