基于NORTA-MCS方法的香港秀茂坪岩坡失稳概率分析

孙元元，周生通，杜晓鹏

(华东交通大学机电与车辆工程学院，江西 南昌 330013)

0 引言

香港秀茂坪岩坡是岩土工程中一个典型的边坡稳定性案例，由于受到随机因素的影响，其稳定可靠性问题一直是国内外学者关注的重点之一[1-4]。目前二阶矩法和Monte Carlo仿真(MCS)方法是分析边坡可靠性的常用方法。其中，前者属于近似解法，虽然计算效率高，但往往会过高或过低地估计可靠度结果。相反，MCS方法虽然计算成本高、效率低，但当选取足够样本数时结果将趋近精确解，是当前工程中获得近似真实失稳概率的通用方法，而且该方法适用于任何规模、复杂度和非线性程度的可靠性问题。

不过，产生符合岩坡随机因素概率信息的样本随机数是基于MCS方法的岩坡可靠性评估正确实施的关键环节之一。在影响岩质边坡平面稳定性的因素中，结构面的抗剪强度、结构面倾角、张裂缝深度、张裂缝充水程度以及地震作用等都可能是不确定性的[3-4]。这些不确定性因素在实际中的概率分布类型往往是任意的，而且因素之间还常存在相关关系，但由于受实际条件限制这些随机因素的完全概率信息多是无法获得的，尤其是在随机因素间完整依赖结构的函数关系表达方面。目前，在众多存在各种限制要求的相关随机数生成方法[5-6]中，NORTA (NORmal To Anything)方法正是满足这一情况的可生成具有任意边缘分布和可行相关矩阵的多维随机数生成算法。它最初由CARIO和NELSON[5]提出，而后GHOSH和HENDERSON[7]讨论了其在高维情况下的性能。从本质上讲，NORTA方法是Nataf变换[8]在相关随机数生成方面的应用，其利用边缘分布和高斯Copula假设[9]来构造物理空间随机因素的伪完备概率信息。

为此，本文将深入探讨联合NORTA方法和MCS方法解决相关随机因素作用下的香港秀茂坪岩坡可靠性问题，给出基于NORTA-MCS方法的可靠度计算基本原理和实现方法，并讨论典型工况下的香港秀茂坪岩坡稳定可靠度及影响规律等问题。

1 NORTA-MCS方法原理

基于MCS方法的可靠度计算关键在于生成给定概率信息的足够样本，之后利用下式估算失稳概率：

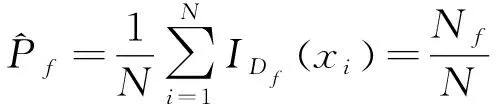
式中：E[·]——数学期望运算符；

Df={X|g(X)<0}——失稳域；

g(X)——极限状态函数；

IDf(x)——失稳域的指示函数，当x∈Df时，IDf(x)=1，否则，IDf(x)=0；

N——总样本点个数；

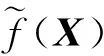
(2)

式中：Φ(·)——标准正态分布的累积分布函数；

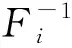
m——随机变量个数。

那么即通过式可将一个维数为m、相关系数矩阵为R0的多维标准正态向量Y=[Y1,Y2,…,Ym]T变换为实际物理随机向量X，而基于此一组服从Y的高斯相关随机数即可转换为服从X的相关随机数。不过需要注意的是，依据Copula理论可知上述变换式等同于在X中引入了高斯Copula假设[9]。由式(2)得X的概率密度函数为：

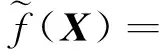
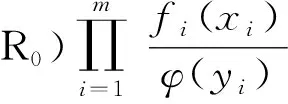
式中：φm(Y,R0)——m维标准正态联合密度函数；

R0——向量Y的相关系数矩阵，可由物理向量X的相关系数矩阵RX得到；

φ(·)——标准正态分布的概率密度函数；

fi(·)——变量Xi的概率密度函数。

式(3)即为基于X的边缘密度函数fi(xi),i=1,2,L,m及其相关系数矩阵RX，并结合高斯Copula假设得到的伪完备联合概率密度函数，亦称为Nataf分布[8]。

但NOTRA方法的难点也是其应用的关键在于能否顺利求解R0并对其进行Cholesky分解。若用ρx,ij表示变量Xi和Xi在相关矩阵RX中对应的元素，那么其与R0中元素ρ0,ij的映射关系为：

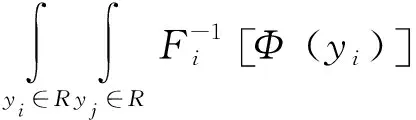
式中：μi,σi——分别是变量Xi的均值和标准差。

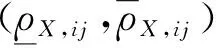
φ(y)dy-μiμj)(5)

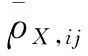
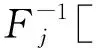
φ(y)dy-μiμj)(6)

综上可知，基于式(4)、(5)和(6)即可计算得到R0，然后在检验并确认R0非负定的情况下，即可利用式(2)中的变换原理生成具有给定边缘分布和相关系数的相关随机数，最后利用这些随机数和式(1)表征的MCS求失稳概率的方法，即可实现结构可靠度计算。本文将这一可靠性分析过程称为NORTA-MCS方法。

2 秀茂坪岩坡的稳定可靠性模型

秀茂坪岩坡的岩体是带有席状节理的未风化花岗岩，属于平面滑动失稳机理，可用图1所示带有张力裂缝的岩坡模型描述其稳定性。基于该模型可推导出秀茂坪岩坡的安全系数S函数表达式为[4]：

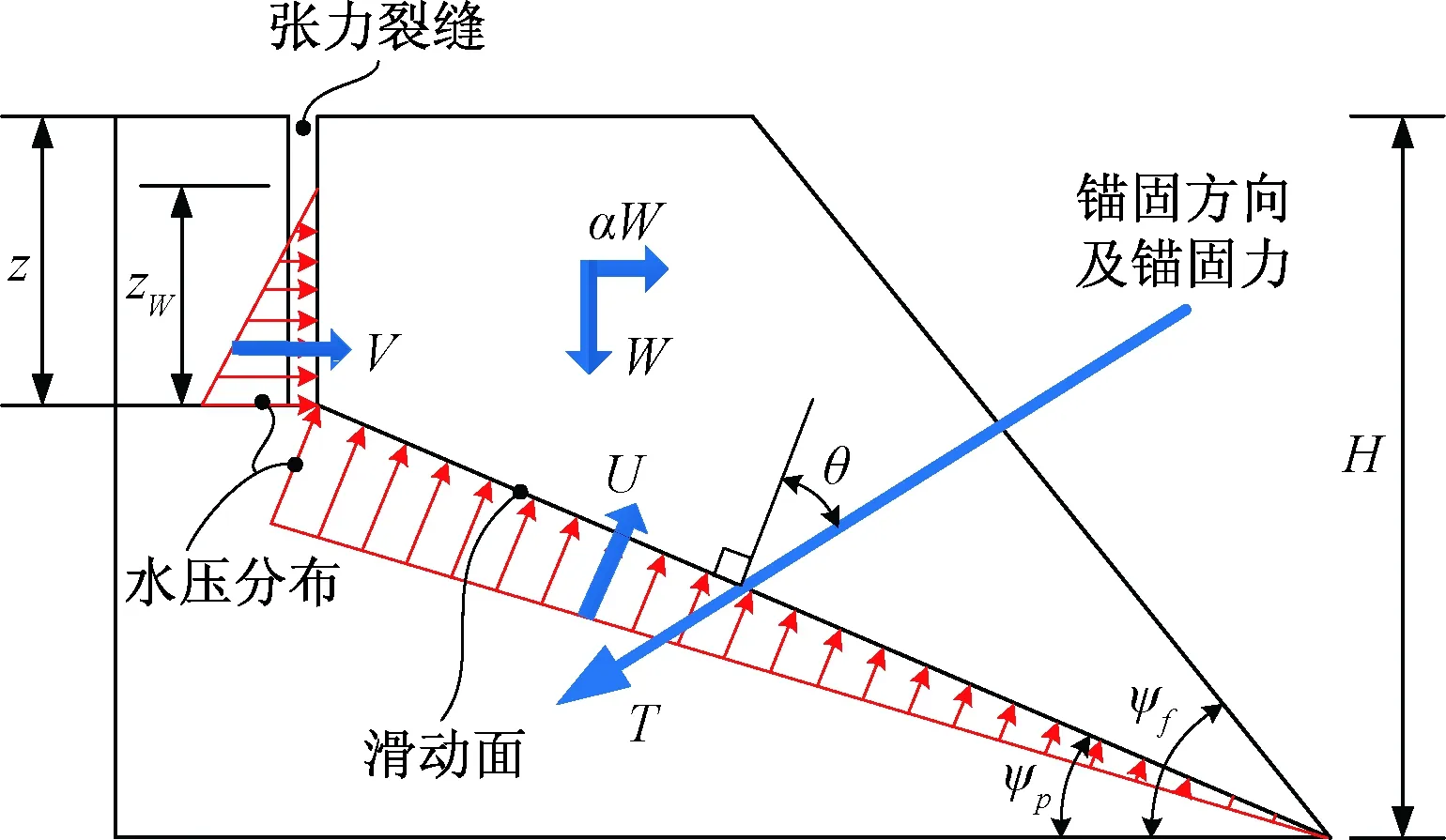
图1 带张力裂缝的秀茂坪岩坡模型Fig.1 Sau Mau Ping rock slope model with tension crack

(7)

式中：A——滑动面单位宽度面积/m2；

W——滑动面上方岩体的重力/t；

U——滑动面上水压产生的上举力/t；

V——张力裂缝中水压产生的水平力/t。

上述各量的计算式分别为：

A=(H-z)/sinψp(8)

W=0.5γH2[(1-(z/H)2)cotψp-cotψf](9)

U=0.5γwrzA(10)

V=0.5γwr2z2(11)

在计算时，式中参数的取值通常为：

H=60 m——总坡高/m；

ψf=50°——坡度/(°)；

ψp=35——滑面倾角/(°)；

γ=2.6t/m3——岩石比重/(t/m3)；

γw=1.0t/m3——水比重/(t/m3)；

c=10t/m3——黏聚力/(t/m3)；

φ=35°——内摩擦角/(°)；

α=0.08——水平地震加速度系数；

T——锚索拉力/t，依据实际情况取值；

θ——拉力倾角/(°)，依据实际情况取值，在自然工况下(即未采取锚固措施)，T=0、θ=0°；

r=zw/z——为张力裂缝的充水程度；

zw——裂缝水深/m，与当地雨水天气有关，计算时一般取为0.5。

从公式中可以看出，该岩坡稳定模型除考虑了岩体重力、滑面摩擦阻力等内部因素的影响外，还考虑了地震、裂缝水压以及人工锚固等外部因素的作用。

在模型参数取为上述定值情况下，可得自然工况下秀茂坪岩坡的安全系数约为1.22。按照传统观点，该岩坡是稳定的且有一定裕度。但现实是模型中的部分参数通常是无法准确测定或确定的，而更应该以随机量来表征这些参数，例如：材料不确定参数c和φ，几何不确定参数z以及外界环境或载荷不确定参数zw、r和α等，研究还发现诸如黏聚力和摩擦角φ之间、充水程度r与张裂缝深度z之间还存在有明显的负相关性[1,4]。按照不确定性传播原理，受不确定性因素影响的秀茂坪岩坡稳定安全系数也将具有不确定性，这就会使得确定条件下认定为安全的岩坡在实际不确定性因素影响下的安全性受到质疑。

为此基于结构可靠性理论，本文以c,φ,z,r,α五个参数为随机参量，构建秀茂坪岩坡稳定可靠性模型，即在式基础上定义极限状态函数：

g(X)=SX-1(12)

式中：S(·)——安全系数函数，即式(7)；

X=[c,φ,z,r,α]T——物理空间不确定参量组成的随机向量。

进而，岩坡失稳概率表达为：

(13)

式中：f(X)——随机因素的联合概率密度函数。

式(7)、(12)和(13)共同构成了香港秀茂坪岩坡稳定可靠性模型。而利用上节给出的NORTA-MCS方法即可实现对该可靠性模型进行求解。

3 结果分析与讨论

表1是秀茂坪岩坡稳定可靠性模型中的随机参数信息，有关取值参照文献[4]，同时考虑实际情况将各个随机参量取为截尾分布类型。在此基础上，本节将基于NORTA-MCS方法分别对自然工况、相关性、锚固措施以及地震动影响下的秀茂坪岩坡稳定性进行分析和对比，最后还讨论了岩坡滑面倾角不确定时的岩坡稳定性问题。

表1 秀茂坪边坡稳定可靠性模型的随机参数

3.1 自然工况时的失稳概率

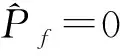
对比可以发现，由于c和φ服从的截尾正态分布与正态分布差别不大，故其的可行域非常接近[-1, 1]区间，且相应Y中的相关系数也与X中的相关系数仅存微小差别。而z和r由于两者分布类型不同，且r服从的截尾指数分布与正态分布差别较大，故可行域缩小明显且变换前后的相关系数差别也比较明显。

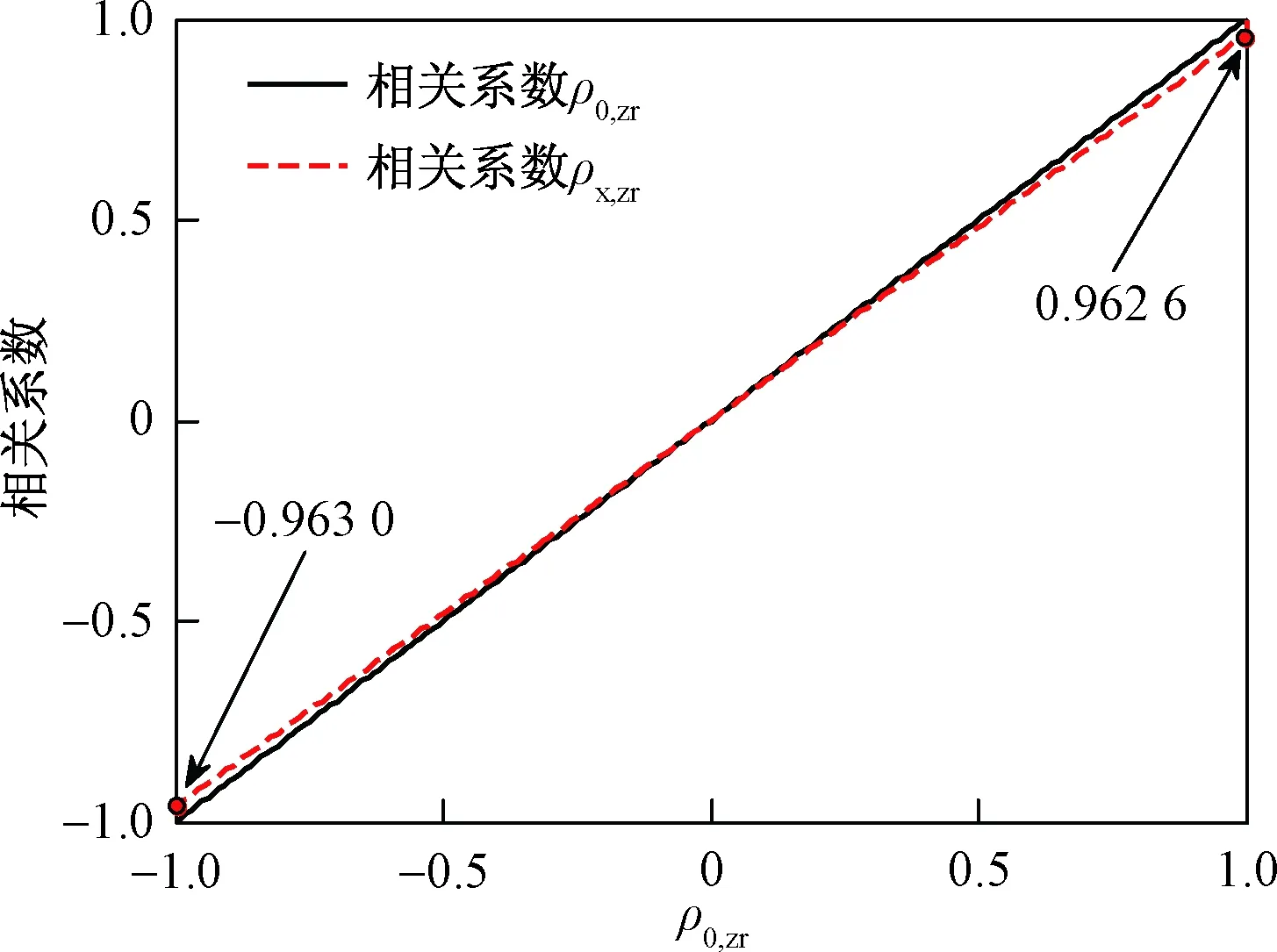
图2 相关系数ρ0,zr和ρx,zr的映射关系Fig.2 The mapping relationship between ρ0,zr and ρx,zr

3.2 相关性对失稳概率的影响

秀茂坪岩坡中黏聚力c与内摩擦角φ、张力裂缝深度z和充水程度r之间具有明显相关性，如果忽略这些相关性或不恰当地指定相关系数就很可能对岩坡失稳概率估算结果造成较大影响。为此，本节分三种情形讨论这种影响：

情形1：ρzr=-0.5，ρcφ=-0.5:0.01:0.5；

情形2：ρcφ=-0.5，ρzr=-0.5:0.01:0.5；

情形3：ρcφ=ρzr=-0.5:0.01:0.5。

其中，情形1考虑了c与φ相关性的变化，由于实际中它们多为负相关性，因而0～0.5的正相关关系是虚设的；情形2考虑了z和r的相关性变化，其中0～0.5的正相关系数可以反映Low指出的由流行地下水位控制的正相关工况；情形3则是一种虚设情形，当两者同时为0时，代表不考虑相关关系的独立工况。由图3可以看到，在[-0.5, 0.5]的相关系数范围内，随着相关系数代数值的变大，三种情况下的岩坡失稳概率均逐步增大且近似呈线性变化。在情形3的独立工况时失稳概率(6.510 8%)约是自然工况(2.21%)下的3倍，可见忽略相关性对秀茂坪岩坡失稳的评估影响非常大。从情形2中的z和r间正相关关系(0～0.5)可以看到，流行地下水位控制下的岩坡张力裂缝充水工况将使得岩坡失稳概率增大，因而实际中非常有必要弄清岩坡张力裂缝充水的原因，正确判断z和r间的相关性质。另外，从变化程度来看，c和φ间相关性的变化对失稳概率的影响程度要比z和r的大。例如：忽略c和φ间相关性(情形1：ρzr=-0.5，ρcφ=0)时，失稳概率由原来自然状态下的2.21%变化为5.075 6%；而忽略z和r间相关性(情形2：ρzr=0,ρcφ=-0.5)时，失稳概率变化为3.633 6%。因而实际中要更注重对岩坡材料相关性的精确测定。需要注意到，图4中失稳概率变化曲线并非光滑曲线，这是MCS仿真结果的随机性导致的。

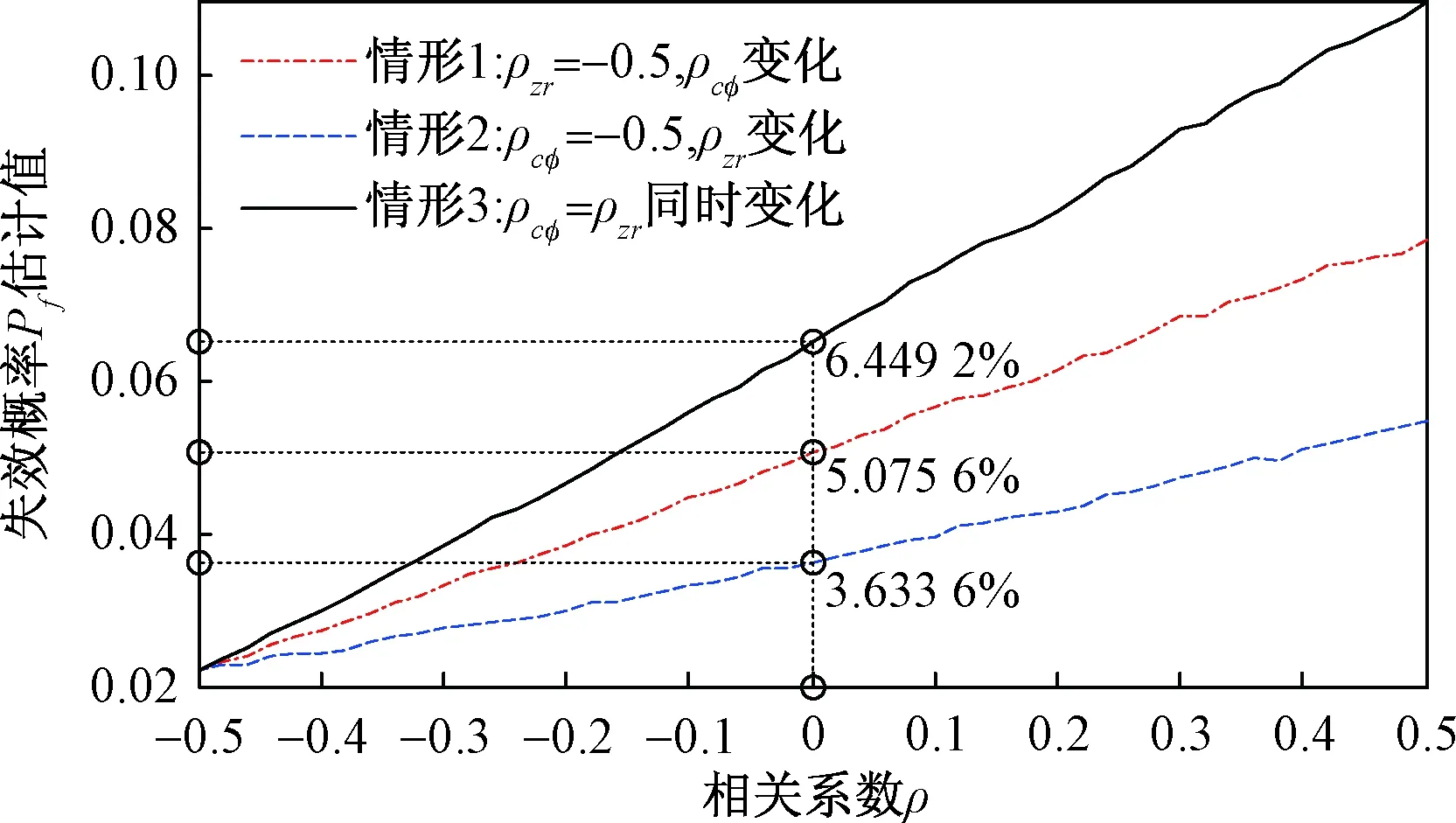
图3 不同情形下岩坡失稳概率随相关系数变化的规律Fig.3 Instability probability of rock slope with the changed correlation coefficients for different cases

3.3 锚固措施对失稳概率影响

作为最常见的岩坡失稳预防措施，本节探讨锚固措施(T≠0时)对岩坡失稳概率的影响规律。取锚索拉力变化范围为T=[0,300](t)，拉力角变化范围为θ=[0,55](°)(即拉力方向按顺时针方向由垂直于坡面变化为水平方向，见图1)，分析秀茂坪岩坡失稳概率随着锚索拉力T及拉力角θ的变化规律，结果如图4所示。

图4 岩坡失稳概率随锚索拉力T及拉力角θ的变化曲线Fig.4 Instable probability of rock slope with the changed anchor tension force T and the inclination θ

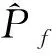
3.4 地震动对失稳概率的影响

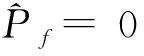
3.5 滑面倾角不确定时的最大失稳概率

通常复杂岩坡的结构面产状较为离散且有限条件下常无法确定其确切分布，此时岩坡稳定模型中的滑面倾角ψP便无法准确确定。这时一种常见的分析方法是：将ψP看作变量寻找岩坡失稳概率最大的滑面，即转化为一个概率最优化问题。本节采用文献[3]中的方法，即：通过在一系列确定性的ψP值之下，得到一系列对应的岩坡失稳概率值；然后拟合得到最大失稳概率所对应的滑面倾角，以该滑面倾角计算岩坡最大失稳概率值。一系列确定性的ψP值确定方法可在HOEK和BRAY给出的滑面临界倾角附近取值，该临界倾角的估算公式为[3]：

αcr=(ψF+φ)/2=(50°+35°)/2=42.5°

式中：ψF——坡度；

一是构建项目成本核算体系。首先，依照作业成本法理论，建立以病人为中心的项目作业库。融入医院自身特色，进一步优化资源动因和作业动因，规范作业流程。建立时间技术难度风险系数算法模型（时间×工作量×技术难度×风险系数）计算作业成本更为合理，也更能体现劳动技术价值，对鼓励医院绩效考核具有指导意义，综合现实情况，更具说服力。

φ——内摩擦角。

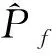
图5 不同滑动倾角时的岩坡失稳概率Fig.5 Instable probability of rock slope for different failure surface angles

4 结论

(1)在高斯Copula假设下，NORTA方法可仅基于随机参量的边缘分布和线性相关系数产生所需的相关随机数，在结合MCS方法的基础上实现岩坡有限概率信息下的稳定可靠性评估。

(2)忽略相关关系的秀茂坪岩坡失稳概率要比自然工况下的高出约3倍；且整个岩坡的失稳概率会随着黏聚力c与内摩擦角φ以及张力裂缝深度z与充水程度r间相关依赖性的增大而增大。因而，正确考虑和评估各变量间的相关关系和相关程度是准确评估秀茂坪岩坡失稳概率的前提。

(3)相比自然工况下的秀茂坪岩坡失稳概率，合理的人工锚固措施可有效地降低岩坡失稳概率，而忽略地震动作用的岩坡稳定性评估结果则会远远高估现实秀茂坪岩坡的安全性，从而埋下安全隐患。在另一方面，当滑动倾角难以确定时，应该将其作为变量来考查秀茂坪岩坡的稳定可靠性，求出最大的失稳概率作为岩坡稳定性预防的决策指标。