基于SVM的冲击地压分级预测模型及R语言实现

2018-09-20陈建宏周智勇

中国地质灾害与防治学报 2018年4期

张曼，陈建宏,周智勇

(中南大学资源与安全工程学院，湖南长沙 410083)

0 引言

冲击地压又称岩爆，是岩体中积聚的弹性变形势能在一定条件下突然释放，导致岩石爆裂并弹射出来的现象。岩爆现象自1738年首次发生以来，几乎在所有矿山开采国家均陆续发生，而目前随着矿山深部开采的推进，岩爆、突水、顶板大面积来压和采空区失稳等灾害性事故频发，严重威胁着矿山生产安全[1]。如何及时准确地判断冲击地压成因，并对其危险性进行准确快速的预测预报，已成为安全生产中亟待解决的重大问题[2]。

目前对于冲击地压危险研究主要集中在现场监测与理论预测研究方面[3-4]。前者[5-7]主要采用如电磁辐射法、地音监测法、微震监测等方法对冲击地压及相关因素进行现场数据收集与分析；后者[8-12]主要是在收集多种影响指标的基础上，采用突变理论、随机森林理论、贝叶斯理论、模糊评价方法等对采场冲击地压进行危险性分级或预测。

尽管目前相关规范、标准[13-14]对于冲击地压的测定、分类有一定的描述，但缺乏具体针对各类矿种的分类量化标准做引导；另一方面，不少文献[15-16]在具体的分级预测中，对模型样本(训练集与测试集数据)的设置较为随意，个人主观性较强。基于以上原因，笔者采用SVM理论对砚石台煤矿采场冲击地压进行分级预测研究，通过复杂的分层随机抽样的技术设置训练集与测试集数据，避免了主观随意性，保证了样本数据的随机性和差异性；同时为了保证模型的可靠性，最终采用多次试验进行验证。

1 支持向量机原理介绍

支持向量机(SVM)是一种基于统计理论的机器学习方法，在统计样本量较少的情况下，亦能通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化。目前已被越来越多的应用于生物工程、岩土工程、水电系统等复杂、非线性以及高维度数据领域中[17]。

本文对于采场冲击地压的分级预测将引入非线性支持向量机。区别于线性支持向量机，该方法主要利用核函数(kernels)通过一种非线性变换将研究问题(采场冲击地压等级与各影响因子之间的复杂非线性关系)转化为高维度空间中的线性问题，进而求解最优分类超平面。

假设样本集为(xi，yi)，i=1，2，…；y=1,2,3,4，其中x为输入变量，y为输出变量，共四类，此时研究问题的超平面方程为：

ω·xi+b=0

(1)

式中：ω——权向量；

b——偏置。

在约束条件上加入一个松弛变量εi，这时的最大间隔超平面称为广义最优分类超平面。则约束条件变为：

s.tyi[(ω·xi)+b]≥1-εi

(2)

对应的优化问题转变为：

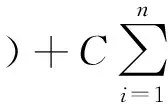
(3)

s.tyi[(ω·xi)+b]≥1-εii=1，2，···n

式中：C——控制惩罚程度的常数；

ε——松弛变量。

在引入Lagrange乘子α、β之后，得到Lagrange函数L( )如下：

(4)

式中：αi、βi——不同输入变量xi与输出变量yi对应的Lagrange乘子。

Lagrange函数L( )在鞍点处是关于ω、ε、b的极小点，此时通过对ω、ε、b分别求偏导，再整理Lagrange函数L( )可得出研究问题对应的对偶问题如下：

maxQ(a)=L(ω,ε,b,α,β)=

(5)

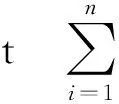
式中：K(xi,xj)——核函数，即ψxi·ψxj在空间H中的映射。

则最优判断函数为：

(6)

目前支持向量机中常用的核函数有：线性核函数(linear)、多项式核函数(polynomial)、径向基函数核函数(radial basis)、神经网络核函数(sigmoid)，通过比较最终判别结果可选出最优模型。

2 基于R语言的采场冲击地压SVM模型实现

2.1 指标选取与数据收集

重庆某煤矿位于四川盆地东南部，井田面积约13 km2，呈南北向延伸，实际生产能力3.5×105t/a。目前随着矿山开采深度逐渐增加，矿岩所受地应力越来越大，围岩破碎程度越来越高，时有岩爆现象产生，矿山安全性问题突出。

采场冲击地压系统是一个高度复杂的非线性系统，各影响指标之间具有极强的非线性关系。结合相关学者的研究[18]，本次选取以下10个指标对冲击地压危险性进行研究：即煤厚(X1/m)、煤厚变化(X2)、倾角(X3/°)、倾角变化(X4)、埋深(X5/m)、瓦斯浓度(X6/m3.min-1)、构造情况(X7)、卸压情况(X8)、顶板管理(X9)、响煤炮声(X10)。

从该煤矿不同工作面共选取36个采场实测数据进行研究，其中24组数据建立样本数据集，剩余12组数据作为预测集，检验模型的预测功能。冲击地压分级预测研究样本数据具体见表1。

表1中煤厚变化(X2)、煤层倾角变化(X4)、构造情况(X7)、卸压情况(X8)、顶板管理(X9)等定性指标划分标准见表2。X12为根据X11(喷出煤岩量)进行的采场地压等级划分，共四个级别，等级越高采场地压越明显。

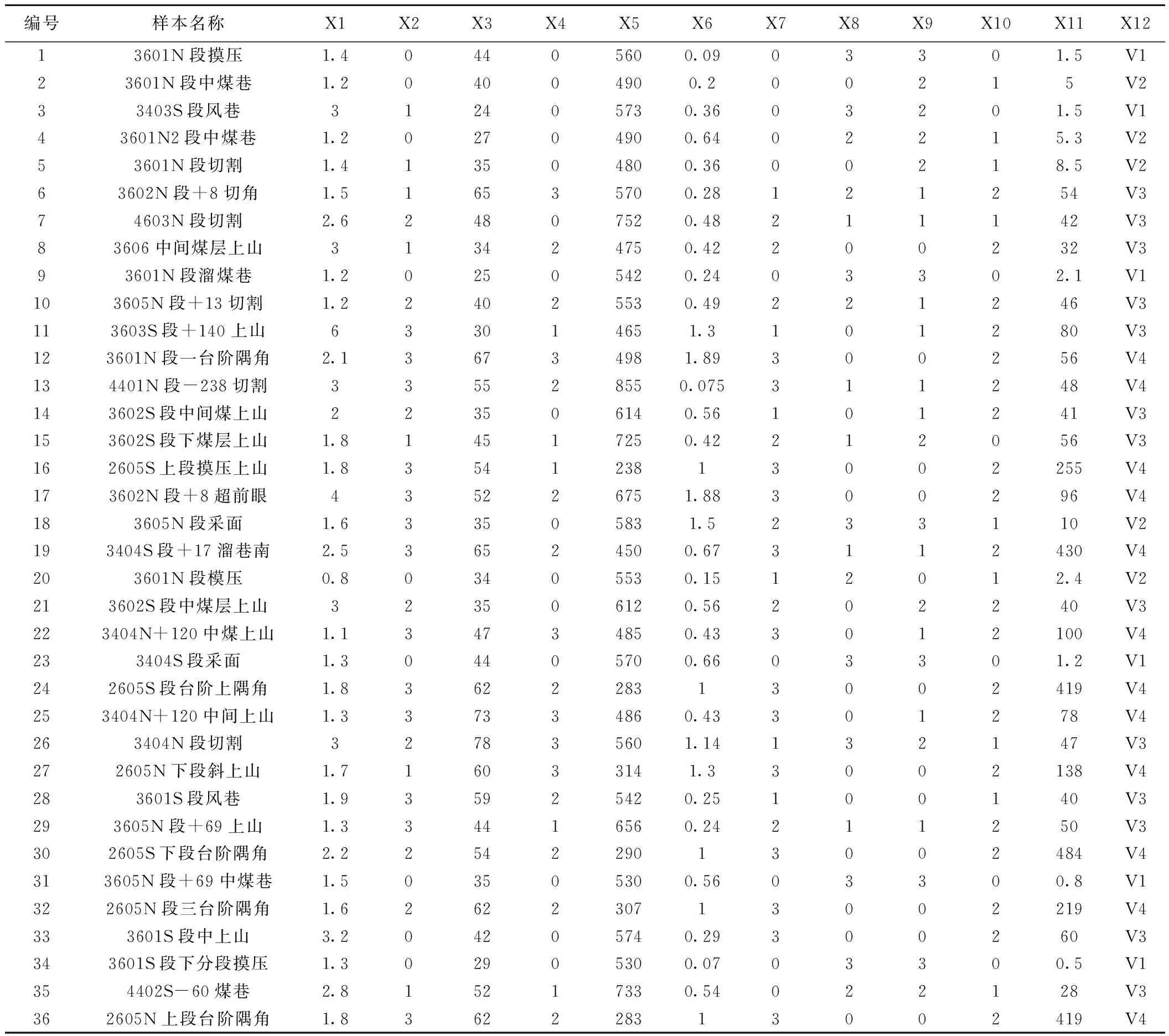
表1 冲击地压分级预测研究样本数据

表2 部分定性指标划分标准

2.2 R语言SVM模型实现

对于采场冲击地压的SVM模型，本文借助R语言，通过调用相关程序包e1071，编写数据分析的代码，进而实现采场冲击地压的分级预测，基本流程见图1。

图1 SVM模型流程图

Fig.1 Flow chart of SVM model

本次模拟主要程序代码如下：

#加载程序包并读入数据

>library(e1071);rock_data=read.table("rockburstedition2.csv",header=T,sep=",");rownames(rock_data)=rock_data$destrict;rock_data=rock_data[,3:14]

#随机分层抽样实现

>c1=round(2/3*sum(rock_data$class.type=="V1"),0);c2=round(2/3*sum(rock_data$class.type=="V2"),0);c3=round(2/3*sum(rock_data$class.type=="V3"),0);c4=round(2/3*sum(rock_data$class.type=="V4"),0);library(sampling);set.seed(58);sub=strata(rock_data,stratanames="class.type",size=c(c1,c2,c3,c4),method="srswor");train_set_x=rock_data[sub$ID_unit,1:10] ;train_set_y=rock_data[sub$ID_unit,12];test_set_x=rock_data[-sub$ID_unit,1:10];test_set_y=rock_data[-sub$ID_unit,12]

#svm模型建立

>model1=svm(train_set_x,train_set_y,type="C-classification",kernel="linear");pred1=predict(model1,train_set_x)

#预测分析

> pred2=predict(model1,test_set_x);table(pred2,test_set_y))

2.3 预测结果分析

2.3.1单次试验结果分析

本次模拟将冲击地压分为4个等级，样本数据中包括训练集样本24个，预测样本12个。通过运行编写的程序，随机抽样得到12个预测样本，预测样本冲击地压等级具体见表3。从表3可知：模型预测准确率达到91.7%，可见本文所建立的SVM冲击地压预测模型评判结果与实际情况吻合。

表3 预测样本预测等级与实际等级对比

表4为采场冲击地压分级预测的混淆矩阵。混淆矩阵中，每行代表预测样本的实际地压等级，每列代表的是SVM模型判定的地压等级。从混淆矩阵可以看出：第一级、第二级、第四级预测样本的实际地压等级与预测等级一致，准确率为100%。实际地压等级为第三级的3404N段切割采场，被误判为第四级，使得第三级的分类误差达到25%。

表4 采场冲击地压分级预测的混淆矩阵

通过对SVM模型中数据降维之后，得到冲击地压等级分布的一个总体观察。从图2中可以看出：地压等级为一级、二级的样本与地压等级为四级的样本之间的特征差异很明显，但部分等级相邻的样本之间的差异较小，这也从另一个角度解释了在模型预测过程中为什么会出现误判。

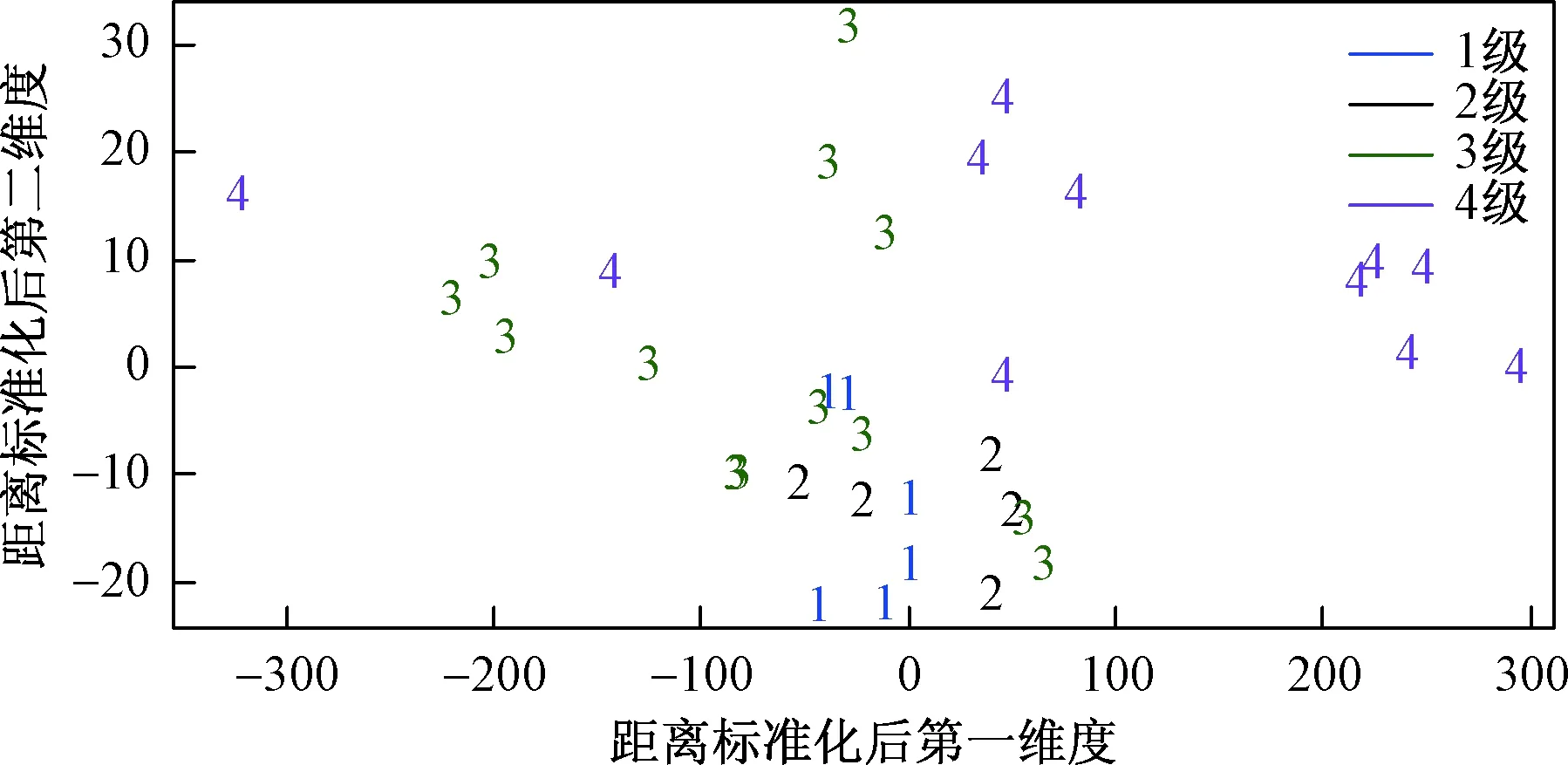
图2 SVM模型冲击地压等级分布图Fig 2 Distribution map of rock burst grade of SVM model

2.3.2随机试验结果对比分析

由于试验次数仅1次，随机可能性太大，不能保证模型的可靠性，笔者根据编写的程序，通过设置不同的随机种子(set.seed)，使得每次抽样产生的训练集与测试集均不同，对模型进行了10次随机试验，预测结果见表5。

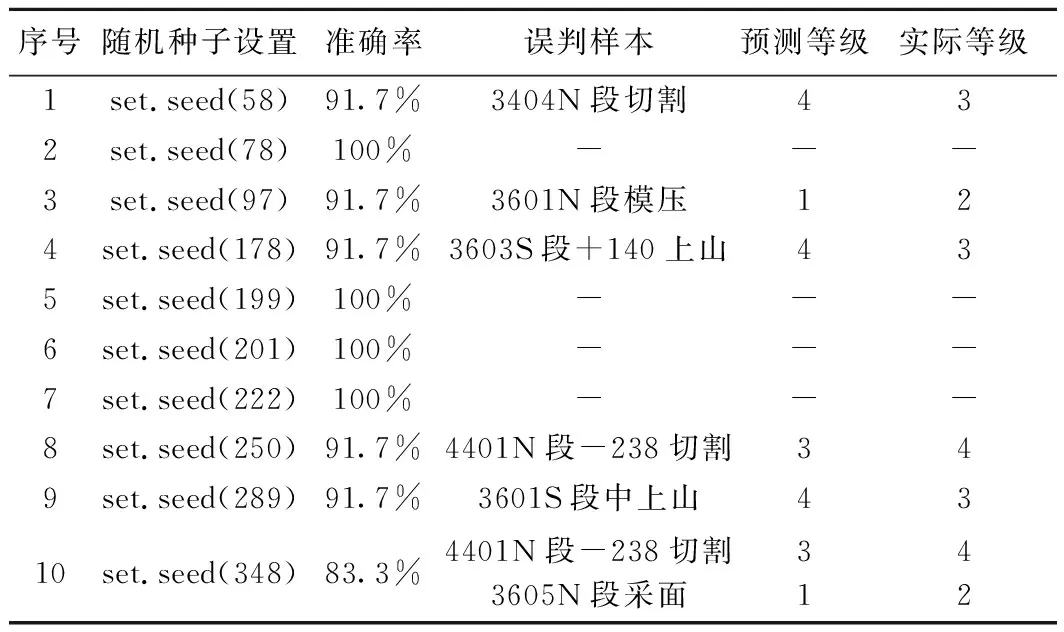
表5 10次随机试验模型预测结果统计Table 5 Statistics of prediction results from 10 random trials

从最终预测结果可以看出：10次试验结果中，有4次预测准确率达到100%，5次预测均只有一个样本预测错误，准确率达到91.7%，另外有1次预测准确率稍低为83.3%，但实际误判样本仅2个。试验结果表明：SVM模型整体预测准确率较高。之所以会造成不同试验结果准确率会不同，主要是因为随机种子的设置，决定着SVM模型的样本组成，而不同的训练集样本数据对模型预测准确率起着较为关键的作用。

另外，通过对比误判样本实际等级与预测等级可以发现：模型并未将地压等级较低的1级、2级样本判别为3级、4级，也并未发生将地压等级较高的3级、4级样本预测为1级、2级的情况。错误主要发生在部分样本差异性较小的1级与2级、3级与4级之间。这也就是说，应用SVM模型进行预测时，即使产生误判，但误判样本的预测等级偏差也不会太大，只是相邻层级的变动。